开坑 啊啊啊

2011

【攻占黄金乡】

不会做，弃疗吧

【最小生成树】

给定一个边带正权的连通无向图\(G=(V,E)\)，其中\(N=|V|,M=|E|\)，\(N\)个点从\(1\)到\(N\)依次编号，给定三个正整数\(u\)，\(v\)，和\(L(u≠v)\)，假设现在加入一条边权为\(L\)的边\((u,v)\)，那么需要删掉最少多少条边，才能够使得这条边既可能出现在最小生成树上，也可能出现在最大生成树上？

考虑Kruskal过程，对于一条边\(e=(u,v,L)\)，仅当所有权值比\(L\)小(严格小)的边加入图中都不能使\(u\)和\(v\)连通时才有必要将\(e\)加入最小生成树中。那么如果\(e_0= (u,v,L)\)在最小生成树中，那么把所有权值比\(L\)严格小的边加入图中都不能使\(u\)和\(v\)连通。现在只考虑权值小于\(L\)的边。问题转化为：删去最少的边使\(u\)和\(v\)不连通。这就是最小割啊。。。

嗯。做完了。调试的时候不要忘了拿极限数据拍一下。第一次提交时数组开小了555。

【串珠子】

orz cyb

其实这题是一个很规矩的状压dp。可惜我就是想不到。

考虑容斥原理，先求出任意连边的方案数之和，再求不连通的方案数。

首先枚举1号点所在的连通块并删掉。设这个连通块内的点集合为\(s\)。发现剩下的块随便连都可以，于是求出了这一部分的答案。然后\(s\)的答案呢?这是个递归子问题。。就可以做了。

具体地说吧。对于集合\(s\)对应的子图，任意连的方案数显然是

\(g(s)=\prod_{i,j\in s}{(c_{i,j}+1)}\)

设\(f[s]\)表示集合\(s\)的子图的答案，那么

\(f[s]=g(s)-\sum_{s_0\subsetneq s}{f[s_0]g(s-s_0)}\)

就可以dp了。通过预处理\(g\)函数，时间复杂度应该是\(O(2^nn^2+3^n)\)吧。

其实好写到爆。

【集合的面积】

其实这玩意有个名字:Minkowski和。

维基百科上的定义就是题目描述中的那玩意。

有一个优美的结论，说把这两个凸包的边混在一起按照极角排序之后首尾相连就是它们的Minkowski和。

所以就是裸题了。1A。

【最长双回文串】

双回文串指形如\(XX^RYY^R\)这样的串。最长双回文串就是一个字符串中最长的双回文串。例如baacaabbacabb的最长双回文串就是aacaabbacabb。求给定字符串\(s\)的最长双回文串。

回文串？manacher先上。在每两个字符之间插入‘#’，求出所有点的回文半径\(r_i\)。

考虑枚举\(X^R\)与\(Y\)的分界点\(k\)，要求\(s_k=\)‘#’，\(XX^R\)的中心\(i\)一定满足\(i+r_i\ge k\)，然后我们最小化\(i\)。右边同样。

想了想，可以\(O(n)\)做。设\(q_i\)表示满足\(x+r_x=i\)的最小\(x\)，计算后缀min即可。另一部分同样处理。

此题在2014集训队论文上有。

【阿狸与桃子的游戏】

http://blog.sina.com.cn/s/blog_a2e4b3970101byum.html

非常神奇的转化思想。

考虑一条边，将边权平分到两个点权上，只有两个点被同一个人选了才对答案有贡献。所以贪心就行了。

我怎么就是想不到呢。

orz 神题

【xmastree】

xmas是圣诞的意思>_<

考虑边分治进行到边$(u,v)$的时候，我们需要统计经过$(u,v)$的同色点对中，距离最小的一对。对于任意的颜色$c$，我们统计$x$子树中颜色为$c$的点到$x$距离的最小值$(x=u$或$v)$。

维护一个很大很大的堆，堆里存着"经过边$(u,v)$，颜色为$c$的同色点对，最小距离为$d$"，且以$d$为关键字。显然只有$O(n\log n)$条信息。

维护一些很小很小的堆，对每条边$u\to v$(你没有看错一条双向边要拆成两条单向边)每个颜色都维护一个堆，对于子树$v$内的、颜色等于指定颜色的点$x$，存储pair <点$x$到$v$的距离,$x$>。堆的个数不会超过$O(n\log n)$个。

现在考虑改变一个点$x$的颜色$c_1\to c_2$时，更新这些堆。与这个点相关的边只有$O(\log n)$条，考虑枚举这些边(假设是$u\to v$，$x$在$v$子树中)，

• 更新小堆：$v,c_1$删除与$v,c_2$添加
• 更新大堆：如果$v,c_1$的最值有变动那么更新$u,v,c_1$的信息；如果$v,c_2$的最值有变动那么更新$u,v,c_2$的信息；

边分治加虚点，虚点的颜色可以取互不相同的负数或什么的。

边分治大法好!!!!!!!STL大法好!!!!!!!map <int, set <int> >大法好

【灭鼠行动】

这题有必要贴代码

#include <cstdio>
#include <set>
#include <algorithm>
//#define DEBUG
using namespace std;

int cab[52][52][4];
int n, m, L, R, p, limit;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
int rt[4] = {1, 2, 3, 0}, lt[4] = {3, 0, 1, 2};

void init_cab(){
  int i, j, orz;
  scanf("%d %d %d %d", &L, &R, &m, &n);
  for (i = 1; i <= m; i++)
    for (j = 1; j <= n; j++){
      scanf("%d", &orz);
      if (orz & 1) cab[i][j][0] = 1;
      if (orz & 2) cab[i][j][1] = 1;
      if (orz & 4) cab[i][j][2] = 1;
      if (orz & 8) cab[i][j][3] = 1;
    }
}

void add_mouse(int x, int y, int face);
class mouse{
public:
  int x, y, face;
  int is_male;
  int turn_tag;
  int status, freeze_rest;

  //walking : 0
  //reproducing : 1 2 3
  //little mice : 7 8 9 10 11

  void grow_up(){
    int p, q;
    if (freeze_rest){freeze_rest--; return;}
    if (status == 0 || status > 3){
      if (cab[x][y][face]){
	x += dx[face], y += dy[face];
      } else{
	p = cab[x][y][lt[face]]; q = cab[x][y][rt[face]];
	if (p + q == 1){
	  if (p) face = lt[face]; else face = rt[face];
	} else if (p + q == 2){
	  turn_tag ^= 1;
	  if (turn_tag) face = lt[face]; else face = rt[face];
	} else{
	  face = lt[face];
	}
      }

      if (status > 4) status++;
      if (status == 12 || status == 4) status = 0;

    } else{
      status++;
      if (status == 3 && is_male == 0){
	for (int i = 0; i <= 3; i++)
	  if (cab[x][y][i]) add_mouse(x, y, i);
      }
    }
  }
} mice[112];
int mice_cnt;
bool deled[112];
int relable[112];

bool reproducable(mouse ljz){
  return ljz.status == 0 && ljz.freeze_rest == 0;
}

void add_mouse(int x, int y, int face){
  mice_cnt++;
  if (mice_cnt > limit){
    printf("-1\n");
    exit(0);
  }
  mice[mice_cnt].x = x;
  mice[mice_cnt].y = y;
  mice[mice_cnt].face = face;
  mice[mice_cnt].is_male = (~face & 1);
  mice[mice_cnt].turn_tag = 0;
  mice[mice_cnt].status = 7;
  mice[mice_cnt].freeze_rest = 0;
}

set <int> micelist[55][55], empty_set;
void del_mice(int x, int y){
  set <int> S = micelist[x][y];
  for (set <int> :: iterator a = S.begin(); a != S.end(); a++)
    deled[*a] = 1;
  micelist[x][y] = empty_set;
}

bool operator < (mouse a, mouse b){
  if (a.x == b.x) return a.y < b.y;
  return a.x < b.x;
}

int sqr(int x){return x * x;}
class weapon{
public:
  int type, t, x, y;
  weapon(){}
  weapon(int ty, int _t, int _x, int _y){
    type = ty; t = _t; x = _x; y = _y;
    if (ty == 3) t += 3;
  }

  void execute1(){
    int i, j;
    del_mice(x, y);
    for (i = 1; i <= L; i++){
      if (!cab[x - i + 1][y][0]) break;
      if (x - i >  0) del_mice(x - i, y); else break;
    }
    for (i = 1; i <= L; i++){
      if (!cab[x][y + i - 1][1]) break;
      if (y + i <= n) del_mice(x, y + i); else break;
    }
    for (i = 1; i <= L; i++){
      if (!cab[x + i - 1][y][2]) break;
      if (x + i <= m) del_mice(x + i, y); else break;
    }
    for (i = 1; i <= L; i++){
      if (!cab[x][y - i + 1][3]) break;
      if (y - i >  0) del_mice(x, y - i); else break;
    }
  }

  void execute2(){
    int i;
    for (i = 1; i <= mice_cnt; i++)
      if (sqr(mice[i].x - x) + sqr(mice[i].y - y) <= R * R)
	mice[i].freeze_rest += 3;
  }

  void execute3(){
    del_mice(x, y);
  }

  void execute4(){
    set <int> S = micelist[x][y];
    for (set <int> :: iterator x = S.begin(); x != S.end(); x++)
      mice[*x].is_male ^= 1;
  }

  void execute(){
    if (type == 1) execute1();
    else if (type == 2) execute2();
    else if (type == 3) execute3();
    else execute4();
  }
} wyh[2000];
bool operator < (weapon a, weapon b){return a.t < b.t;}

void reconstruct(){
  int i, j = 0, x, y;
  for (i = 1; i <= mice_cnt; i++)
    if (!deled[i]) relable[++j] = i;
  for (i = 1; i <= mice_cnt; i++) deled[i] = 0;
  for (x = 1; x <= m; x++) for (y = 1; y <= n; y++) micelist[x][y] = empty_set;
  for (i = 1; i <= j; i++) mice[i] = mice[relable[i]];
  mice_cnt = j;
  for (i = 1; i <= j; i++)
    micelist[mice[i].x][mice[i].y].insert(i);
}

char fach[10] = "NESW";
void print(int t){
  //printf("%d\n", mice_cnt);
#ifdef DEBUG
  int i;
  printf("|        micecnt = %4d    t = %3d       |\n", mice_cnt, t);
  printf("+-----+----+----+---+------+------+---+--+\n");
  printf("|mouse|xpos|ypos|fac|status|frezre|sex|tt|\n");
  for (i = 1; i <= mice_cnt; i++){
    printf("+-----+----+----+---+------+------+---+--+\n");
    printf("|%5d|%4d|%4d| %c |%6d|%6d| %c | %c|\n",
	   i, mice[i].x, mice[i].y, fach[mice[i].face], mice[i].status, mice[i].freeze_rest, mice[i].is_male ? 'M' : 'F', mice[i].turn_tag + 48);
  }
  printf("+----------------------------------------+\n");
#endif
}

int Time;
int main(){
  int i, ty, t, x, y, j, k, w, o; char sex, dir;
  init_cab();
  scanf("%d", &mice_cnt);
  for (i = 1; i <= mice_cnt; i++){
    scanf("%d %d %c %c", &mice[i].x, &mice[i].y, &dir, &sex);
    if (dir == 'N') mice[i].face = 0;
    else if (dir == 'E') mice[i].face = 1;
    else if (dir == 'S') mice[i].face = 2;
    else mice[i].face = 3;
    if (sex == 'X') mice[i].is_male = 1;
    else mice[i].is_male = 0;
  }
  mice[i].turn_tag = mice[i].status = mice[i].turn_tag = 0;
  for (i = 1; i <= mice_cnt; i++)
    micelist[mice[i].x][mice[i].y].insert(i), deled[i] = 0;

  scanf("%d %d", &p, &limit);
  if (mice_cnt > limit) return printf("-1\n"), 0;
  for (i = 1; i <= p; i++){
    scanf("%d %d %d %d", &ty, &t, &x, &y);
    wyh[i] = weapon(ty, t, x, y);
  }
  sort(wyh + 1, wyh + p + 1);

  scanf("%d", &Time);
  w = 1;
#ifdef DEBUG
  printf("+----------------------------------------+\n");
#endif
  for (t = 0; t <= Time; t++){
    while (w <= p && wyh[w].t == t){wyh[w].execute(); w++;}
    reconstruct();
    for (x = 1; x <= m; x++)
      for (y = 1; y <= n; y++)
	if (micelist[x][y].size() == 2){
	  set <int> :: iterator it = micelist[x][y].begin();
	  j = *it; it++; k = *it; it++;
	  if (mice[j].is_male == mice[k].is_male) continue;
	  if (reproducable(mice[j]) && reproducable(mice[k])){
	    mice[j].status = mice[k].status = 1;
	  }
	}
    print(t);
    o = mice_cnt;
    if (t != Time){
      for (i = 1; i <= o; i++) mice[i].grow_up();
    }
    reconstruct();
  }
  printf("%d\n", mice_cnt);
  return 0;
}

感谢hzwer的程序，不然我不可能调出这个题。。

经验：

学会输出中间结果

在考场上遇到这种东西就弃疗

教训：

只算这么多老鼠就行了，不要把下一秒出生的老鼠也算上

理解题意很重要

清空数组要彻底。比如说处理死老鼠，deled[i]表示第i个老鼠是不是死的，o是活老鼠数+死老鼠数，n是活老鼠数，最后把deled清空成0的时候我只清空了deled[1..n]，就跪了。应该保证清空之后deled[1..sizeof(deled)]都是0，清空deled[1..o]即可。

还有一个地方

    o = mice_cnt;
    if (t != Time){
      for (i = 1; i <= o; i++) mice[i].grow_up();
    }

grow_up这个函数是可以改变mice_cnt的值的，于是如果直接for (i = 1; i <= mice_cnt; i++) mice[i].grow_up();那么就跪了。

【篱笆】

【比特集合】

对于一个单独的$k(0\le k<16)$，我们令$cnt_{k,i}$表示模$2^{k+1}$等于$i$的数的个数。考虑为护$cnt_k$这个数组。

INS和DEL单点修改。

ADD区间移位。记录移位的量即可。

QBIT区间查询。

开15个树状数组梳妆数组就好啦。

猛然发现复杂度是$O(k^2)$一次询问的。。常数小就是王道

【潜入虎穴】

为了测量清澄上的栈空间我交了一个

1. int travel_plan(int N, int M, int R[][2], int L[], int K, int P[])
2. {
3. int s[2020202][3];
4. }

有5分。。。(估计第一个点的答案是0)

然后吐槽小强copyIOI的原题。。

大致就是令$f_s$表示起点为$s$时的答案，那么$s$不是终点时

$f_s=\text{secmin}_{(s,t)\in E}(f_t+w(s,t))$

其中$\text{secmin}$表示某集合中的次小值。

那我就嘴巴一下dijkstra版和spfa版=。=

dijkstra的时候会把节点分成两个集合，一个是答案已经确定的$D$，一个是答案未确定的$U$，每次从$U$中选一个“可能答案”最小的$x$放入$D$，然后用$x$去更新其他点。

这里的话“可能答案”就是所有更新的次小值。

spfa的时候总是用次小值去更新别人。还有，这个spfa貌似是有问题的，小数据拍不死，大数据一拍就挂，可以骗55分。

。。。谁知道为什么这个spfa有问题。。。

【数树】

先跪小强和7爷。对于第10个测试点，$N=6002，M=4$。小强是故意的

问题转化为每个点度数小于等于$m$，有$\frac{n-2}{m-1}$个点的无标号无根树的个数。

无根树计数问题：化为有根树计数问题。

那么我们先解决$n$个点的无标号有根且每个点度数不超过$m$的树的计数问题。

$f_{i,j}$表示这样的有根树的个数。它有$i$个点，根的度数为$j$。考虑知道了一个$f_{i,m-1}$，它会更新后面的$f_{k,l}$。具体地说枚举$x$(考虑我们将要更新的$f_{k,l}$，根节点的子树中有$x$个大小为$i$的子树。由于我们没有计算$>i$的答案，所以这些子树时大小最大的那$x$个)。

$$f_{k,l}\leftarrow f_{k,l}+f_{k-xi,l-x}\binom{f_{i,j}+x-1}{x}$$

现在考虑无根树。

树分两种：有一个重心(gyz说的“质心”。。说“重心”说习惯了)的和有两个重心的。两个无根树同构的充要条件是

• 两棵树都只有一个重心，且把重心提根，两有根树同构。或
• 两棵树都有两个重心，且把两棵树的某个重心分别提根，两有根树同构。

如果我们在上面只用$<\frac{n}{2}$的$i$来转移，那么得到的$f_{n,m}$就是单重心树的个数。双重心个数是$[n\equiv 0(\mod 2)]\binom{f_{\frac{n}{2},m-1}+1}{2}$。

2012

【模积和】

$$\bigl(\sum_{i=1}^n(n\mod i)\bigr)\bigl(\sum_{i=1}^m(m\mod i)\bigr)-\bigl(\sum_{i=1}^n(n\mod i)(m\mod i)\bigr)$$

三个部分中$(n\mod i,m\mod i)$这个pair的取值个数都只有$O(\sqrt{n})$。

所以$O(\sqrt{n})$爆搞即可。

【楼房重建】

$h_i\leftarrow H_i/i$，问题变成单点修改$h$和

询问for(x=0,ans=0,i=1;i<=n;i++)if(h[i]>x)x=h[i],ans++的最终ans。

我们把$h$称作高度(而不是$H$)。

建立线段树，定义$Q(h,x)$为在节点$x$的所有楼房的前面加上一个高度为$h$的楼房，那么可以看到多少楼房(不包括$h$)。定义$T_x$为节点$x$中最高的高度，$l_x,r_x$为$x$的两个子树。

那么如果$h\ge T_{l_x}$，那么$Q(h,x)=Q(h,r_x)$；否则$Q(h,x)=Q(h,l_x)+Q(T_{l_x},r_x)$。

对每个点$x$维护一个$q_x=Q(T_{l_x},r_x)$。

询问直接$Q(0,root)$即可。

修改的话考虑一步步往上更新，更新$x$的时候$q_{l_x},q_{r_x}$都是正确的值，我们只需要调用$q_x=Q(T_{l_x},r_x)$即可得到正确的$q_x$。$T$这种东西也可以随手维护吧。

如果硬要问我复杂度我会说$O(m\log^2 n)$。。。

【序列染色】

特判$2k>n$的时候请输出0。

我们枚举$i\dots i+k-1$表示序列中一段都是B的元素，$j\dots j+k-1$表示序列中一段都是W的元素。

会算重。。我们强制令$i$是最小的下标，满足$i\dots i+k-1$都是B；$j$是最大的下标，满足$j\dots j+k-1$都是W。

我们的序列长成这样：

|不存在连续$k$个B|连续$k$个B|任意|连续$k$个W|不存在连续$k$个W|

$f_{i,j}$表示前$i$个字母中没有出现连续$k$个B，且最后一个字母是$j$的方案数。$f_{i,j}$都是从$f_{l,\bar{j}}\dots f_{i-1,\bar{j}}$转移过来的。其中$\bar{j}=(j==\text{B}?\text{W}:\text{B})$，$l$反正是一个可以$O(1)$算的数。dp的思路大概就是枚举：所有字母都是$j$的后缀长度为$s$，然后从$f_{i-s,\bar{j}}$转移过来，而合法的$s$构成一个区间。

前缀和优化一下就可以$O(n)$求出$f$数组啦。

同理用$g_{i,j}$表示后$i$个字母中没有出现连续$k$个W，且最后一个字母是$j$的方案数。转移也可以写出来。

令$S_i$表示$1\sim i$中X的个数。

考虑枚举上述的$i,j$。如果$i\dots i+k-1$都不是W，$j\dots j+k-1$都不是B，且$j\ge i+k$，那么这对$i,j$对答案的贡献就是

$$f_{i-1,\text{W}}\times 0.5^{S_{i+k-1}}\times g_{j+k,\text{B}}\times 2^{S_{j-1}}$$

从大到小枚举$i$，可行的$j$不断增多。

所以用了这么多手段把这个题搞到$O(n)$啦。

【长跑】

orz 陈许旻

刚学LCT的时候想用LCT干掉这个题。。脑补了很久发现复杂度好像不对。。我果真是too young

这题允许离线。

首先我们可以发现加入的边可以分成三种：

1. 加入了不改变强连通性的；
2. 加入了会把一些强连通块合并成一个的；
3. 加入了会使两个连通块连通的。

无视所有1类边，用并查集处理所有3类边，河蟹掉所有答案是-1的询问。那么我们的树是固定的，问题相当于有这样三种操作：

1. 把$x$到$y$路径上的所有点合并成一个点；
2. 修改权值；
3. 求$x$到$y$路径上的点权和。

考虑只有2和3的时候怎么做，用链剖维护一个线段树。。然后好像不能扩展到操作1。。(说不定可以，我没有仔细想>_<)$O(\log^2 n)$一次操作太慢了吧

标解用的是神神哒dfs序，dfs开始的时候放一个$val[i]$，结束的时候放一个$-val[i]$，询问$x$到$y$的路径和($y$是$x$的祖先)变成了询问$y$开始的位置~$x$开始的位置的数的和。

现在考虑有操作1的时候，假设我们要合并$k$个点$a_1,a_2,\dots,a_k$，并且$a_i$是$a_{i+1}$的父亲。在原来数列的位置上，我们可以把$val[a_1]$换成$\sum_{i=1}^kval[a_k]$($-val[a_1]$进行相同操作)，$val[a_i](i>1)$变成$0$，然后把所有点“真实指向的点”(一个并查集维护)赋值为$a_1$。

这题真心好写。幸亏没有入lct的大坑(雾)

庆祝清澄于8.13日下午恢复正常~虽然比较卡~

bzoj上：$O(n\log^2 n)$跑了6808ms，$O(n\log n)$跑了5264ms。呵呵

当然也有自己常数写丑的原因。。

一个点是$(x,y)$，圆心是$(x_0,y_0)$，点在圆心内当且仅当$x^2-2xx_0+y^2-2yy_0\le 0$。这就是一个半平面。

。。。直观的解释，就是：这个半平面的边缘是$(0,0)$与$(x,y)$的中垂线，半平面不包含$(0,0)$。

问题变成：每次插入一个点，询问一个半平面是否包含所有点。

数据范围挺吓人的。。好像是50w。

cdq分治搞一搞就好了，$O(n\log^2 n)$多出来的log是排序，我们使用归并排序就可以去掉那个log了。然而并没有什么卵用

cdq分治见许昊然论文。

吐槽。。

都是5264ms没有差别。。两个题是画风完全不一样的两个题啊。。。

【跨平面】

平面图的对偶图的最小树形图。

人们常说，简单的题意往往暗藏杀机=_,=

其实也不算难写啦，关键是我忘了最小树形图的模板

【序列操作】

线(ka)段(chang)树(shu)练习题。

咦不是clj吐槽过这个题的数据范围只能开到10000吗

线段树每个点维护$21$个值表示从这个子树内选$k$个数的乘积的和是多少，update可以做到$O(20^2)$。

取负数的话奇数项取负数即可。加上一个数的话推导一下(找找规律，与组合数有关)。

能用到的组合数就那么几个，预处理出来即可。

复杂度$O(n\log n\times 20^2)$。被卡常了只有90分。upd11.26:过了。少用乘法，多用加减。

【麻将】

暴力过不了，然后就弃疗了。

以下用“三张”表示三张相同的牌，“三连”表示三张点数连续的牌。

考虑$c_{m,x}(x\not\equiv 1(\mod 3))$表示从1m~9m中选出$x$张牌，每张牌都属于对子/三张/三连，且至多一个对子的方案数。

$d_{m,x}$表示从1m~9m中选出$2x$张牌，每张牌属于对子/三张/三连，至多一个对子，且每张牌选的个数都是偶数的方案数。

当然还有$c_{s,x},d_{s,x},c_{p,x},d_{p,x},c_{c,x},d_{c,x}$。

那么通过简单的背包可以求出一般胜利状态的个数。

七对子的个数也可以dp。

有的状态既是一般又是七对子，这些状态的个数可以参考$d$数组。容斥掉即可。

国士无双跟前面的不重复，直接算即可。

还有。。答案不会爆long long哦。。

获得成就：在对拍快死的时候切断对拍(幸亏保留了数据233)

还有一个坑点(只会坑到我这样的傻逼)。。我用python算组合数(怕中间过程爆long long)结果爆python的double精度了。。这两门语言的double并没有什么区别。。

神神的dp。

$f_{i,j}$表示若$i$回合被boss攻击前剩下$j$点HP，至少要回多少次血。这个显然可以做。

然后考虑我们除了回血之外还做了些什么：要么使用MP相关的技能(法术、MP药水)，要么使用SP相关的技能(普通、特技)。而我们并不需要考虑所有技能使用的顺序，只需要考虑一类技能使用的顺序。例如说，$a_i$表示MP相关的技能，$b_i$表示SP相关的技能，那么我们先后使用$a_1b_1b_2a_2a_3b_3$和先后使用$a_1a_2a_3b_1b_2b_3$的效果是一样的。发现这一点是本题的关键。

$g_{i,j}$表示使用$i$次MP相关的技能，使用完之后拥有$j$的MP，至多扣boss多少血。

$h_{i,j}$表示使用$i$次SP相关的技能，使用完之后拥有$j$的SP，至多扣boss多少血。

转移方程随手写。

如果我们令$P_i$表示使用$i$次技能最多扣boss多少血，那么$P_i=\max_{j+k=i,a\ge 0,b\ge 0}g_{j,a}+h_{k,b}$。然后假设用了$t$局打败boss，最终剩$h$点HP，那么我们最多扣boss$P_{t- f_{t,h}}$点血。

就可以统计答案了。

【保护古迹】

建立一个汇点。枚举我们需要保护哪些古迹，抠出它们所在的域，这些域是对偶图中的一些节点，把这些节点与汇点之间连$+\infty$的边。其他的边，对偶图中怎么加就怎么加。求最小割即可。

对偶图中的最小割，就是把原图中一些点与无穷域隔开的代价最小的回路(平面上的一堆多边形)。(理会一下吧，就像平面图最小割=对偶图最短路，实质应该是一样的)

所以这题就是$O(2^p)$次网络流即可。

【树】

开始在想这题怎么过掉菊花树。。然后发现好像$O(n^2)$是下界。。

然后仔细看了一眼题目。。“小Q手中有一棵二叉树”

f**k

一条链的情况就是快排吧。。。然后YY出一个“树上快排”=、=

快排是什么?每次从待排序区间中随机出一个数，找出比它大的数和比它小的数，然后对各自两边排序。

复杂度咋证?我不知道=_=

那么套到这个题上我们定义solve(S)表示已知$S$是一个子树内节点的集合，合法地调用submit来删除$S$中的所有点。可以随机选出一个节点$x$，找出$x$的子树和$x$的祖先$p_1,p_2,\dots,p_l$。然后用快速排序可以给这些祖先按祖孙关系排序。对于剩下的点可以二分找出它与$x$的LCA是哪个$p_i$。那么我们对每个$p_i$确定了它的子树(子树中不包含$p_i$)，对这$l+1$个子树(别忘了$x$的子树哦)递归即可。

复杂度咋证?我不知道=_=猜想是$O(n\log^2 n)$的。

实测可以过97分。。链的点过不去。。链的点卡快排，请使用stable_sort。。妈蛋

【阳光】

upd已弃疗特殊情况太tm多了精度太tm不能忍了真的写不出调的要吐血了谁tm来救救我

TAT

明显地可以转化成这个模型：给出一些区间，它们都包含于$[-\pi,\pi]$，且两两不交。再给出一个$d$，其中$m=\frac{2\pi}{d} \in \mathbb{Z}$。求一个$x<d$使得$x,x+d,x+2d,\dots,x+(m-1)d$中，被某个区间覆盖的数尽量多。

考虑枚举$x$，可能的$x$一共只有$O(m+\text{区间个数})$种，可以从小到大处理所有可能的$x$，堆/排序都可以。

2013

【破冰派对】

我做法是$O(n^3/64)$的。(不过这题有小于$O(n^3)$的做法吗?)

对于一个人，只有他认识的人两两互相认识(即组成一个团(clique))，他才有可能是参与者。因为如果一个人是参与者，那么他认识的人都是工作人员，而工作人员之间是要两两互相认识的。同理一个人不认识的人两两互不认识，他才可能是工作人员。于是我们可以在$O(n^3)$的时间复杂度内求出每个人可不可能是参与者/工作人员。这部分可以压位，就是$O(n^3/64)$了。

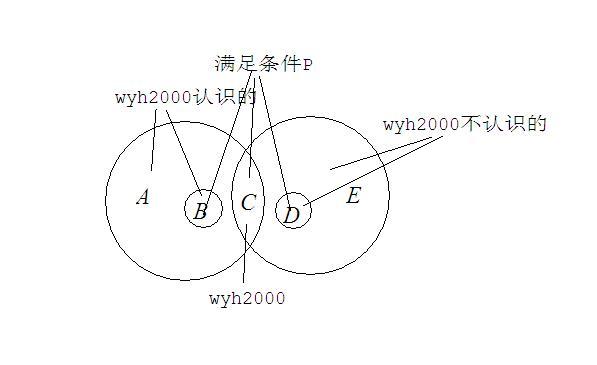
假设不存在一个既有可能是参与者，又有可能是工作人员(称作“满足条件$P$”)的人，那么问题就很简单了，结束。否则设这个人是wyh2000。所有人可以被分成3类：wyh2000认识的、wyh2000不认识的，和wyh2000自己。前两类又可以细分：满足条件$P$的，和不满足的。这样我们把人划分成了5类：ABCDE。

那么$B$和$C$中的所有人，至多一个人是参与者，因为参与者互不认识，而$B\cup C$是一个团。同理$C$和$D$中的所有人，至多一个是工作人员。我们把$B$中的参与者和$D$中的工作人员称为“特殊人物”。由于$C$不是工作人员就是参与者，所以“特殊人物”至多一个。

枚举谁是“特殊人物”，然后可以确定wyh2000是工作人员还是参与者。

如果没有“特殊人物”，可以枚举wyh2000的身份。

答案不会超过$n+1$。做完这个题我都不记得那个模数是13中间夹几个0

【冒泡排序】

令$l_i$表示数字$i$(不是排列的第$i$位)前面有多少个比$i$大的数。

考虑题目中给出的代码。$i$变化一位，意味着$l_x\to \max(0,l_x-1)$。

证：注意到指针$j$的性质：任何时候$a_j$都是$a_1\dots a_j$中的最大者。假设$l_x\ne 0$，那么在$j$指向$x$所在位置(设$a_p=x$，那么这个位置就是$p$)之前，$a_{p-1}>a_x$(不然$l_x=0$)。而此时$l_x$没有变化。然后我们会执行$\text{swap}(a_{p-1},a_p)$，$a_{p-1}$对$l_x$的贡献没了，所以$l_x\to l_x-1$。这一轮中之后的变化不影响$l_x$。而如果$l_x=0$的话，命题是显然成立的。

而一轮中swap执行的次数就是$\sum_{x=1}^n[l_x>0]$。

我们可以确定一个$k_0$：执行$k_0$次swap时的$i$不等于执行第$k_0+1$次swap时的$i$(就是在不同轮)；且接下来的$k-k_0$次swap可以一轮搞定。获得$k_0$轮之后的$l$数组，然后恢复出$a$数组，暴力模拟剩下几轮即可。

【扑克牌】

考虑将一些牌拆成一些链，每条链的牌颜色要求不同(所以点数就必须相同)，我们统计$a[x][y]$表示以花色$x$为开头花色$y$为结尾的牌的数目。一点也不显然的，合法的$a$的数目不会很多。这部分怎么暴力怎么搞吧。。翱犇说“轻松跑进1s”，那是在手写map的时候我才能跑进3s。

用$dp[i][a]$表示『考虑点数小于等于$i$的牌拆成一堆链，满足这些链中以花色$x$为开头花色$y$为结尾的链恰有$a[x][y]$条』的方案数。

对于一个合法的$a$我们用$dp[\text{K}][a]$乘以『以$a$为邻接矩阵的图的欧拉回路个数(这个可以dp)』，加起来就是答案。

可能这题的题解比较抽象不好讲。。。推荐看topcoder srm448 div1 level3(TheCardLineDivOne)这个题的题解。。或者这个题陈老师代码啥的都挺好。。

【存不下】

$f_{i,j}$表示长度为$i$的01串，运行到$H=j$的时候至少输出多少个1。

考虑令$S=24$。记录$f_0$(这个不需要记录)$,f_S,f_{2S},\dots,f_{S\lfloor\frac{n}{S}\rfloor}$的dp值。这个是不会爆空间的。

现在考虑求方案，如果已知$f_{Si,j}$是合法方案，那么可以暴搜前面$S$个字符是$0$还是$1$然后推得$S$步之前的$j_0$，检查$f_{S(i-1),j_0}$转移这么多步之后是不是$f_{Si,j}$。求方案的总复杂度$O(\frac{n}{S}\times 2^{S})$。

但是实际效果是，$S=25$只有暴力分(或者暴力分都没有)。。事实上我的方法是对特定的$m$使用特定的$S$(大概可以看成$S=O(m)$)，比如说$S(m=20)=24,S(m=15)=15$等等。再加少许常数优化就可以通过本题辣。

Q：做小强的题有什么好处    A：找借口浪费时间

【杰杰的女性朋友】有一天讲课的时候clj给我们推荐了这道题说这是个好题

令$f_{i,j}$表示$i\to j$的边的数目，显然就是要你求$(1+f+f^2+\dots+f^d)_{x,y}$。(我们用$1$表示单位矩阵。。$I$和$O$表示输入的两个矩阵)

然后可以得到$f=OI^T$。

所以就是求$\sum_{i=0}^d{(OI^T)^i}$。。。

$n\times n$的矩阵做乘法是不可忍受的!

答案等于$1+O\bigl(\sum_{i=0}^{d-1}(I^TO)^i\bigr)I$。$k\times k$的矩阵乘法可以做。

由于我们只需要求出这个矩阵的某一个元素，所以求出了矩阵$\sum_{i=0}^{d-1}M^i(M=I^TO)$之后可以$O(k^2)$算出这个元素。现在关键是求$\sum_{i=0}^{d-1}M^i$。

考虑倍增。。$F_i=M^{2^i},G_i=\sum_{j=0}^{2^i-1}M^j$，那么有递推式

$$F_i=F_{i-1}\times F_{i-1},G_i=G_{i-1}(F_{i-1}+1)$$

预处理$O(nk^2+k^3\log d)$，询问复杂度$O(k^3\log d)\text{ per query}$。

【理想国】

见雅礼双神的《两个冷门图论算法》最后几页。orz 翱犇。

首先第一问，考虑对每一对边算贡献，分为两条边无公共点与两条边有公共点讨论，发现贡献都是$\frac{2}{3}$。所以第一问就是$\frac{m(m-1)}{3}$。

第二问的话，考虑一堆区间$(l_i,r_i)$两两相交，那么一定有$\max(l_i)<\min(r_i)$。也就是选出两个集合$S,T(S \cap T=\emptyset)$，最大化$\sum_{i\in S,j\in T}[(i,j)\in E]$。显然$T=V\backslash S$是最好的。所以就是最大割了。

用的随机乱搞求最大割，好像答案比标程优(大雾)。

正解是什么。。带花树相关。。请自行英文wiki maxcut。(我反正不感兴趣=。=)

【mex】

并不会做。

考虑离线。首先找出所有答案为$0$的询问。考虑把序列中的$0$抠出来，比如说

$$a_{i_{0,1}}=a_{i_{0,2}}=\dots=a_{i_{0,k_0}}=0$$

再令$i_{0,0}=0,i_{0,k_0+1}=n+1$。那么如果一个询问区间被严格地包含在某个$(a_{i_{0,j}},a_{i_{0,j+1}})$中，那么这个询问区间的答案就是$0$。

把这些答案是$0$的区间去掉之后，考虑所有的$1$，比如说

$$a_{i_{1,0}}=a_{i_{1,1}}=\dots=a_{i_{1,k_1}}=1$$

那么严格包含于$(a_{i_{1,j}},a_{i_{1,j+1}})$的询问，答案就是$1$。

。。。以此类推。

我们需要支持一种操作：遍历某个矩形内的所有点并删除。

。。。并不会做。

。。。k-d树暴力搞就行了。。。

。。。想想就觉得比较靠谱。。。

。。。虽然我是卡着时限过的。。。

另外好像这题出自sillycross

http://blog.sina.com.cn/s/blog_97a3fe860101er4g.html

upd.关于这题正解，参考xhr的题解(链接在上面)

其实就是每次删掉的都是$l$固定时$r$最小的几个区间。所以线段树即可。

【结合律】

而我在虐抽代。（大雾）

没有看懂证明。。据说错误率是$(7/8)^k$的，其中$k$是随机次数。。

我只随了7次，怎么看怎么不靠谱。。

每次随机三个数组$a,b,c$(实数也好int也好)，检查$d_i=\sum_{(j\times k)\times l=i}a_jb_kc_l$和$e_i=\sum_{j\times (k\times l)}a_jb_kc_l$是否相等。

注意到$d,e$都是可以$O(n^2)$算的，这题就可以做了。

然后怎么$O(n^2)$呢，就是令两个序列$x,y$的乘积$(x\times y)_i=\sum_{j\times k=i}x_jy_k$，那么$d=(a\times b)\times c$，$e=a\times (b\times c)$，而乘积是可以$O(n^2)$做的。

很神奇的思路。

【字符串生成器】

AC自动机。Trie图。

$f_{s,i}$表示出现过的串是集合$s$，现在到达自动机上点$i$，期望还要走多少步。

转移有环，需要高斯消元。

这是一个分层图，按照$s$分层。每一层只有$O(nL)$个节点，可以$O((nL)^3)$高斯消元。不同层之间可以直接算，反正没有环。

复杂度$O(C2^nn^3L^3)$吧。

【fx】

首先感谢wyh2000教会我这么神的dp。

设$B$是一个$n$位十进制数。

令$f_{i,j,k}$表示这样的数$x$的个数：$x$是$i$位数，$x\le\lfloor\frac{B+1}{10^{n-i}}\rfloor$($k=0/1$表示小于/等于)，且$x$的权值减去$(\lfloor\frac{A}{10^{n-i}}\rfloor)$的权值等于$j$。所以我数组开的f[222][22][2]

注意到$j\ge 10$意味着$x$的权值一定大于$C$的权值；$j\le -10$意味着$x$的权值一定小于$A$的权值。我们只管$j\in (-10,10)$的情况。

枚举下一位之后可以很轻松地完成转移。

算答案的话。。转出去了就记为答案。

【动态树】

空间限制1G是什么鬼

首先考虑$K=1$的情况，容易发现可以$O(\log n)$一次询问。具体见下面。

然后考虑$K\le 5$，我们把所有有关的点抠出来建立一棵虚树就可以知道需要询问哪些边，然后一次次询问就行了。。

不过上述算法只是嘴巴选手的狂欢。。我并没有写。。因为我不会虚树

我用的是容斥。。一次询问是$O(k2^k\log n)$的，傻逼死了。就是考虑一堆边都经过的所有点(以下简称“交集”)，它一定是一条链或者是空集。一根树枝设祖先是$p$，孙子是$c$，把所有的$p$中高度最低的作为交集的祖先(如果各个$p$不是祖孙关系，那么交集为空)，所有$c$的LCA作为交集的孙子。如果孙子比祖先高，那么交集为空。

写完暴力拍的时候突然发现我是在拿一个多项式暴力拍一个指数正解。。雾

“下面”：子树add链求和。

我们考虑add $x$时在$x$处打一个标记$b_x$，那么一个点的真实权值是$v_x=\sum_{p\text{是}x\text{的祖先}}b_p$。链求和转换为求$\sum_{p\text{是}x\text{的祖先}}v_p$。设$d_x$表示$x$的深度，发现只需要维护$\sum b_x$与$\sum d_xb_x$，变成单点修改链(一个点到根)查询。

再转模型，每个单点修改我们改成子树修改，链查询就是单点查询了。利用dfs序可以变成线性结构上的问题，一个线段树就水过了。当然有像我一样的可以把数列差分，写树状数组。

【猴子挖矿】

2014

【玛里苟斯】

消出线性基，删掉其他元素，不影响答案。

$k>2$的时候$n\le 21$，可以暴力。

$k=1$的时候发现就是某一位是1的话这一位的贡献就是0.5，否则就是0。

$k=2$的时候枚举$i,j$，然后求$i,j$位都是$1$的概率。无视其他位做一个dp即可。

【主旋律】

$f_s$表示$s$导出子图的答案。用总的答案数减去：枚举把$s$分成若干集合，每个集合是一个强连通分量，然后求每个集合的$f$值乘起来blabla的答案。

写成式子就是

$$f_s=2^{|E(s)|}-\sum_{t_1,t_2,\dots t_k\text{是}s\text{的一个划分}}A(t)\prod_{i=1}^kf_{t_i}$$

其中$|E(s)|$是$s$导出子图的边数，$A$表示一个图的DAG子图个数。

为了方便起见，我们令$\text{PA}(s:t_1,\dots,t_k)$表示$t$是$s$的一个划分(就是$s$的一些子集，两两不相交，并集为$s$)，$\text{SPA}(s:t_1\dots,t_k)$表示$t$是$s$的一个严格划分，且$t$中至少有两个集合(就是，$t=\{s\}$是不能算的)。

记号和名词都是随手乱YY的。。

像上一个式子实际上$t$是严格的划分，即

$$f_s=2^{|E(s)|}-\sum_{\text{SPA}(s:t_1\dots,t_k)}A(t)\prod_{i=1}^kf_{t_i}$$

然后考虑$A(s)$，简单容斥

$$A(s)=\sum_{t\subseteq s}(-1)^{|t|+1}A(s\backslash t)ways[s\backslash t \to t]$$

其中$ways[A\to B]$表示起点在$A$内终点在$B$内的边的个数。。。哦不，2的这么多次方

迭代一步，发现

$$f_s=2^{|E(s)|}-\sum_{\text{SPA}(s:t_1\dots t_k)}(\sum_{t_0\subset t}(-1)^{|t_0|+1}A(t\backslash t_0)ways[s\backslash t_0\to t_0])\prod_{i=1}^kf_{t_i} (1)$$

$$f_s=2^{|E(s)|}-\sum_{t_0\subset s}\sum_{\text{PA}(t_0:t_1\dots t_k)}\sum_{\text{PA}(s\backslash t_0:t'_1\dots t'_k)}{(-1)^{k+1}A(t')ways[s\backslash t_0\to t_0](\prod_{i\le k}f_{t_i})(\prod_{j\le l}f_{t'_j})} (2)$$

(注：上面两个式子中$t_0$代表的东西不一样。。$(1)$式中$t_0$是$s$的划分的一个子集。。或者说$s$的一个子集的划分方案。而$(2)$式中$t_0$直接代表$s$的一个子集，我们希望把$t_0$的所有划分方案一起计算；$(2)$式中有$t_0\neq \emptyset$的限制(因为$A$的递推式中就是这样的)；还有因为$(1)$式的限制是$\text{SPA}$所以$t_0=s$的时候是$\text{SPA}(t_0:t_1\dots t_k)$)

两个东西显然是可以分开的啊啊我擦

$f_1(t)$表示$t$的所有划分方案中，$(-1)^{k+1}\prod_{i\le k}f_{t_i}$的和。

现在式子就简单了。。

$$f_s=2^{|E(s)|}-\sum_{t_0\subset s}f_1(t_0)(2^{|E(s\backslash t_0)|})ways[s\backslash t_0\to t_0]$$

关于那个$2^{|E(s\backslash t_0)|}$我解释一下。。其实是

$$\sum_{\text{PA}(s\backslash t_0:t_1\dots,t_k)}A(t)\prod_{i=1}^kf_{t_i}$$

然后注意到这个数就是$2^{|E(s\backslash t_0)|}-f(s\backslash t_0)+f(s\backslash t_0)$(因为$f$的定义中用的是“$\text{SPA}$”，而PA可以看成SPA与『不对集合进行划分』的和)

还是要强调一遍特殊条件。。$t_0\neq \emptyset$，并且$t_0=s$的时候$f_1$的划分方案是严格的。。

不过怎么求$f,f_1$呢?假设我们知道了$t\subset s,t\ne s$的所有$f_t,f_1(t)$，我们要求$f_s,f_1(s)$。

首先求出$f_1(s)$吧，$f_1(s)=\sum_{t\subset s}-f_1(t)f_{s\backslash t}$，其中$t\neq s$。

然后可以求出$f_s$了。

如果想直接看dp方程的话看红色字就行了。最后一个问题，$ways$这个数组的优化。。直接dp，状态$O(3^n)$转移$O(1)$。

写这个题的时候我$ways$预处理错了，调dp调了很久，简直炸掉了。

【奇数国】

求欧拉函数的话，只需要维护积与质因子分布情况。积可以直接用线段树维护，质因子分布压了个位之后也可以用线段树维护。

【简单回路】

假设我们询问所有的可能的简单回路个数，那么可以用插头dp。f[s][i][j]表示dp到点(i,j)，轮廓线上的插头状态为s。转移什么的有点复杂，讨论讨论就好。

考虑一次询问，经过某条横边的个数，枚举这条边所在的一个轮廓线的状态，把dp值乘一下即可。

关于轮廓线dp。。我们定义状态为一个括号序列(三进制数)。。具体见cdq的论文。

【卡常数】

题如其名啊。

k-d tree裸题，定期重建，调调参，卡卡常。

不重建的话。。我没有试过，不过看上去也可以过。

【矩阵变换】

设行$i$中选择数$a_i$，那么条件4可以改成，不存在两行$i,j$，使得$a_i$在$j$中出现的位置比$a_i$晚但是比$a_j$早。

考虑稳定婚姻问题(= =)，这意味着行喜欢靠前的数，数喜欢靠后的行。

【sum】

最后看到题解的我眼泪掉下来

我们只需要关心$\lfloor\sqrt{drd}\rfloor$是奇数的个数。然后问题变成求

$$\sum_{d=1}^n\lfloor d\sqrt{r}\rfloor-2\lfloor d\frac{\sqrt{r}}{2}\rfloor$$

两部分独立求。举个例子我们要求$\sum_{d=1}^n\lfloor dr\rfloor$，其中$r\in \mathbb{R}$。

就是直线$y=xr$下面的整点的个数。。

于是就变成了裸的exexgcd。

【router】

对于一个正则表达式我们希望构建出它的NFA。然后是爽爽的讨论。

定义一个过程$\text{create}(str,type,s)$为给定一个类型为$type$的字符串$str$，我们以$s$为开始状态，构建一个NFA并返回其结束状态。为了方便结束状态只有一个。(如果有多个的话可以拿$\epsilon$边来连到同一条边上)

首先如果$str$是空串，那么显然直接返回$s$即可。

$\text{create}(str,\text{Regexp},s)$如下：新建一个节点$a$作为结束状态。用|符号把$s$切成若干段，对每一段执行$t=\text{create}(str,\text{Alternative},s)$，并把$t$用$\epsilon$边连向$a$。最后返回$a$。

药剂$(a,b,c,d)$用点$(\frac{a}{a+b+c+d},\frac{b}{a+b+c+d},\frac{c}{a+b+c+d})$代替，那么题目变成了:给出$N$个点，要求它们的三维凸包$C$，并支持两种询问共$M$个：

1. 给定一个点$P$，是否有$P\in C$?
2. 给定一个半空间$H$，它与$C$是否有交集?

但是我只看懂了题解中凸包的部分。。TAT

(声明：这一章节中所有图片来自AC_Aerolight的ppt)

凸包的表示方法：一堆有向的三角面片(用三角面片的三个顶点和面的法向量来表示，法向量指向凸包外)。设面的三个顶点为$A,B,C$，法向量为$v$，我们称$p$在面外当且仅当$(p-A)\cdot v>0$。此外我们还需要维护凸包上的所有边，每条边有两个方向(即拆成两条)，每个方向维护其右侧的面是谁。(点、边、面的个数都是$O(n)$级别的)

首先用增量法求凸包。那么我们按照某种顺序$P_1,P_2,\dots,P_n$将点加入凸包。假设我们有一个凸包$CH(P_{r-1})$，加入一个点$P_r$之后我们想得到新的凸包$CH(P_r)$。那么我们需要找到$P_r$看得到$CH(P_{r-1})$的哪些面($P_r$在这些面外)，并把它们删掉。然后我们找到那些【一侧的面被删了，一侧的面没有被删】的边，对每条这样的边新建一个面(包含原来的两个顶点和$P_r$)。新的凸包就做好了。

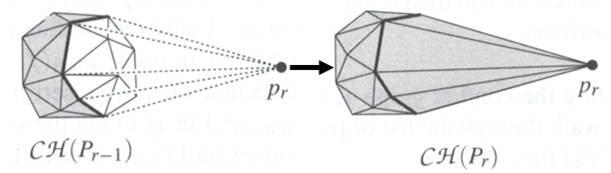
注意到现在我们的复杂度是$O(n^2)$。。。会跪。。。不妨考虑一下我们要干什么：

1. 寻找$P_r$看得到的所有面；
2. 寻找所有地平线(上图中的黑边)；(这个可以在计算1的时候顺带得出)
3. 加入一些面。

我们维护一个叫做『冲突图(conflict graph)』的东西。这是一个二分图，左边的点代表输入中的、未加入凸包的点，右边的点代表当前凸包中的面。如果点$p$在面$f$的外面，那么将$p$与$f$连一条边。

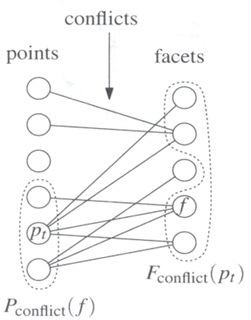
寻找$P_r$看得到的面，就直接在conflict graph中遍历$P_r$的邻边即可。然后把$P_r$加入凸包，conflict graph中删掉$P_r$。关键是加入一些面，我们需要对每个pair(未加入的点,待加入的面)判断并连边。如下图，考虑加入一个面$f=ep_r$，其中$e$是已经加入凸包的边，$p_r$是刚刚被加入的点。在此之前$e$两旁的边连接的是面$f_1,f_2$。那么一个点在$f$外，可以推出它要么在$f_1$外要么在$f_2$外。

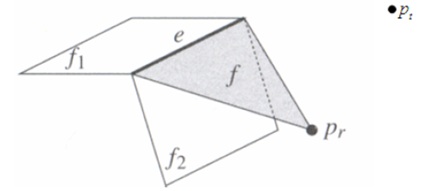
于是求出了凸包。

询问的话，盾哥的题(dai)解(ma)大概是这么写的：令$C=CH(P_4)$。可以直接询问点是否在$C$中，如果在那么返回yes。否则考虑点在$C$的哪些面的外面，随便揪出一个这样的面$f$，如果$f$没有被删除过那么答案显然是no。设$f$是在加入点$P_r$的时候被删除，那么置$C=CH(P_r)$，继续前面的步骤(询问点是否在$C$中的时候只需要访问加入$P_r$时加入的面即可)，直到$C=CH(P_n)=$最终凸包。

。。。复杂度?不会证。。应该是靠谱的，毕竟有人说有理论计算机科学家证出来了。。

【虫逢】考察点：智商

假设我们把所有可能的$M$个元素设定一个随机的大小关系，考虑一个变形虫的基因$S$，记最小的那个基因为$\text{min}(S)$，次小的基因为$\text{sec}(S)$。若两个变形虫是同源的，那么它们最小基因相同的概率是$1/3$。如果不是同源的，那么它们最小基因相同的概率为$1/L$(我没有仔细算，应该是不会大于$1/L$的)。

如果我们同时取最小值和次小值，，那么概率分别是$p_{\text{succ}}=1/9$和$p_{\text{fail}}=1/L^2$。

这样处理一遍之后，我们找出了部分同源的元素，换一个大小关系($a,b$)，继续找即可。

首先考虑判同源的次数。显然成功的为$n$次。失败的次数为处理的次数乘以$O((Np_{\text{fail}})^2)$。这里失败的次数为处理的次数乘以$O(1)$。(这也解释为什么要选最小值和次小值，因为如果只选最小值的话失败次数是$O(N)$ per 处理 的)

然后考虑处理的次数，设$C(n)$表示处理的次数。一次处理我们可以判掉$\frac{n}{9}$个元素，即$C(n)=C(\frac{8}{9}n)+1$，所以$C(n)=O(\log n)$。。也就是说失败的判断不是复杂度瓶颈。

那么扫描的复杂度呢?一次扫描是$O(nL)$的，即$T(n)=O(nL)+T(\frac{8}{9}n)$，可以得到$T(n)=O(nL)$吧。

所以总的复杂度是$O(nL)$的。常数大概为$10$。

【玄学】

=========================一种能A的暴力=============================

考虑以操作建线段树，一个节点内存的是只考虑这个节点内的操作，序列的第$i$位会变成多少(用$ka_i+b$表示)，注意到对于某连续的一段来说$k,b$都是一样的，所以只要维护每一段即可。段数不会超过操作数的两倍，所以线段树中的东西数是$O(q\log q)$的。

修改的话直接补全线段树，复杂度不关心，反正不会超过两个$\log$。

询问的话区间询问。。对于一个节点直接二分即可。。复杂度好像就是$O(\log n\log q)$，不过uoj上目前的rank1(ertyuio神犇)就是这么写的(吧)。

=============================正解================================

首先考虑每个询问都执行所有操作的情况(即，$i=1,j=$目前操作数)。对序列维护一个线段树，每个节点维护的标记表示“加入到这个节点的所有操作的总和”。每次加入一个区间就在线段树上进行区间修改即可。

然后扩展一下，线段树的每个节点维护一个平衡树，以时间为key直接存储所有操作，标记下放的时候就把这个平衡树复制一份，两个平衡树分别与左右儿子合并即可。因为儿子平衡树中的操作总是比父亲平衡树中的操作要晚，所以是可以合并的。

询问操作，既然是单点询问，就把所有祖先的平衡树拉出来一个一个询问，因为黑体字所示性质，只有$O(1)$个平衡树我们真的要用$O(\log q)$的时间往下走来询问。

使用的平衡树，因为要复制所以要可持久化，而亲测可持久化treap是不可以的(常数大概乘2，AVL都只能卡过treap肯定过不了)(见http://uoj.ac/submission/26916，当个笑话看一看)，所以只能用可持久化AVL。结果我还是帮std垫了底

修改操作的复杂度为$O(\log n\log q)$，询问操作的复杂度为$O(\log n+\log q)$。

【文学】

乱搞有$90$分我会说

给出$n$个集合，要求选出权值和最小的一些集合，使得它们的并等于所有集合的并。

慢着，zjoi好像也有这么个题。不管怎么说，这个题(不是说文学，是说普通的set-cover)是NPC的。

zjoi那个题数据强一些，乱搞搞不到这么多分。

下面进入正题

首先把半平面取反，变成选权值和尽量小的半平面使得交集不包含任意一个点。

然后考虑半平面交为空的情况。Helly's Theorem说，对于$d$维空间中的$n$个凸集，如果任意$d+1$个集合的交不为空，那么$n$个集合的交不为空。考虑半平面交为空，即存在$3$个半平面它们的交为空，那我还要其他半平面干什么。直接$O(n^3)$枚举，$O(p)$检验一下即可。

然后考虑半平面交不为空的情况，dp就好了。

题解上说了，在枚举凸包上的一个点后,每个半平面在交中,“挡住”的点的极角序是连续的。“极角序”显然指的是枚举凸包上的点之后，以这个点为原点的极角序。

这句话应该这么理解，对于凸包的每条边我们可以指定一个区间$[l,r]$，使得区间的并是所有的点，且每条边不包含其区间内的所有点。注意是序列的区间不是环的区间。

举个例子

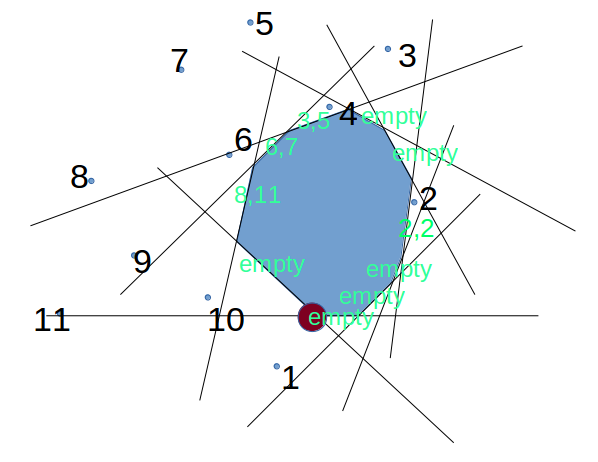
(如果还不能理解的话建议看std。。std写得很清楚)

(上图中起点是那个大大的红点，被绿色empty挡着一半的那个)

不过作为一个数学捉鸡的sb，我表示并不会证明T_T

所以枚举凸包的起点(某两个半平面的交点)，然后令$w_{i,j}$表示用一个半平面覆盖极角序$[i,j]$中的所有点的最小代价，然后$f_i$表示覆盖$1\to i$的最小代价即可做到$O(n^2)$的dp。算上枚举的复杂度，总复杂度$O(n^2p^2)$的，大概可以过吧。

复杂度：$O(n^3p+n^2p^2)$。

2015

【遥远的星系】

对于一个询问 首先求出两点距离$d$，然后询问它们所在连通块中所有环的环长gcd $g$。如果目标长度为$c$，可行当且仅当$g=0$且$d=c$，或$g\ne 0$且$g|(d-c)$。

维护距离：$dep(x)$为根到$x$的距离，那么$dis(x,y)=dep(y)-dep(x)$。因为从LCA走到根再从根走到LCA的权值是$0$。加入一条树边的时候，启发式合并，更新小块的$dep$。据说带权并查集也可以做。

维护gcd：每加入一条非树边就求出它对应的环的环长，更新这个连通块的gcd。因为每一条非树边对应一个“基环”，每个环的长度是一些“基环”的和或差，所以只要知道这些“基环”长度的gcd就可以了。(←口胡)以及，加入一条树边的时候，合并两个连通块的gcd。

复杂度$O(n\log n+m\alpha(n)+m\log w)$。

【恐怖的奴隶主】

令$v_i=\prod_{j=1}^i u_j$。我觉得能在考场上想出这个转换的人肯定很神。

$$v_i=v_{i-1}(a+\frac{b}{u_{i-1}}+\frac{c}{u_{i-1}u_{i-2}})=av_{i-1}+bv_{i-2}+cv_{i-3}$$

令$\alpha,\beta,\gamma$为$x^3=ax^2+bx+c$的三个根，那么存在实数$a,b,c$，使得

$$u_i=\frac{a\alpha^i+b\beta^i+c\gamma^i}{a\alpha^{i-1}+b\beta^{i-1}+c\gamma^{i-1}}$$

假设$\alpha>\beta>\gamma$。

所以$u$数列是收敛的，如果$a=b=0$那么极限是$\gamma$；如果$a=0,b\ne 0$那么极限是$\beta$；否则极限是$\alpha$。

直接上python高精度数即可。。出题人说只要本题有任何精度误差就会爆炸。。比如把$a=0$算成$a=10^{-100}$，极限就从$\beta$或$\gamma$变成$\alpha$了。

也可以直接开long double，看上去收敛的时候就break。风险较大，期望得分0~100不等

【小Q与找茬】

首先离散化，然后用线段树套链表维护。线段树的每一个节点$[l,r]$维护一个表，保存所有$x$坐标在$[l,r]$之间的点。这个表按照$y$坐标排序。

对于一个询问$[x_1,x_2]\times [y_1,y_2]$，我们找到$[x_1,x_2]$对应的线段树中的节点，在这些节点中二分。

复杂度$O(\log^2 n+k)$一次询问，其中$k$是你报上去的节点个数。

这题卡常数。。不过也不是很卡，大概按照std的写法，内存要连续访问，就好了。

其实std弱爆了(雾)

【静态仙人掌】

按照myy的讲法就是首先构一棵根的最短路树，然后处理出每个询问的集合bitset。(就是$x$到根的最短/长路上的点集、$x$的子仙人掌内的点集)

怎么处理呢?最短路很简单，就是最短路树上点到根的路径。

最长路的话，如果一个点$x$的父亲(最短路树上的)不是它所在环的根(或者$x$压根不在某个环上，或者$x$就是某个环的根)，那么它的最长路就是它父亲的最长路异或上他自己；否则它的最长路是它父亲的最长路或上整个环。

子仙人掌。。我们丢掉最短路树，对于一个点我们给它的儿子节点以及儿子环上的所有节点连边，那么“子仙人掌”就是子树?这样就可以考虑dfs序啦!

给每个点搞出dfs序编号然后求出每个点到根的最长/短路对应的bitset。相当于每次xor上一个bitset，然后询问一段区间的1个数。暴力就是$O(n/w)$一次询问的，不虚。($w=32$)

最后的问题：空间。我们直接考虑128M的空间限制。

考虑用分块维护bitset，每$H(n)$个bit分成一个块，内存中有很多个长度为$H(n)$的块。一个长度为$n$的信息由$\frac{n}{H(n)}$个内存中的块来表示，记录这样一个信息只需要记录$\frac{n}{H(n)}$个块的编号。说白了就是可持久化块状数组。

咦，居然有人用可持久化数据结构来卡空间

求最短路/最长路的时候我们每次对当前bitset修改$O(1)$个元素然后变成下一个bitset。使用的int个数是$O(H(n)/w+\frac{n}{H(n)})$的(一个新的块状数组加一个新的块)。

令$H(n)/w=\frac{n}{H(n)}$有$H(n)=\sqrt{nw}$。

时间复杂度：$O(\frac{nq}w)$

空间复杂度：$O(n\sqrt{\frac{n}{w}})$

【斗地主】

考虑最暴力的想法，$f_{i,j,k}$表示己方的牌为$i$，对方的牌为$j$，对方上次出的牌为$k$时己方的最大得分。实现的时候，$i,j$可以是状态压缩一样的bitset(牌集)，$k$的话用pair(类型，长度(如果是顺子)，关键牌的点数)就可以记录了。

加一个记忆化吧。

我第一次实现的版本(见main1.cpp)可以很快地跑出第一个点，稍微等几分钟可以跑出第二个点，跑一个小时可以跑出第三个点。不过由于没有写飞机带翅膀所以只有19+17+14分(uoj submission 40019)。(upd：main1.cpp在处理顺子的时候有bug，懒得调了。main2.cpp改过来了)

考虑一个优化：二分答案。对于搜索树的每个叶子节点，我们只需要知道它$<$答案或$\ge$答案。在搜索牛牛的时候，只要发现$\ge$答案的决策就可以退出；在搜索小伙伴的时候，只要发现$<$答案的决策就可以退出。反正可以加优化的地方就加优化吧。见main2.cpp。

用时：第三个点3.5min，第四个点67min。确实快了不少。分数是75=19+19+19+18(这应该是不考虑飞机带翅膀的真实分数了)

有一天我跑了一天的第5个点，后来发现爆零了。。真是悲伤。

main1:http://yunpan.cn/c39XIDjpGgbZM （提取码：7810）

main2:http://yunpan.cn/c39Xit8TBKVhw （提取码：7d9d）

【园子里】

首先判无解，$h_i$最小的那些柱子如果$t$都是$0$，那么存在无解的柱子：只要是能够到达(任意一个$h_i$最小的柱子)的柱子就是无解的。其他的可以照样dp嘛(不过答案好像都是$1$)。

然后对于正常情况 我们进行dp。$f_i$为$i$的答案，那么

$$f_i=1+\frac{\sum_{h_j\le h_i-t_i}f_j}{\sum_{h_j\le h_i-t_i}1}$$

因为$h$比较小所有可以$O(n+h)$做一遍排序，确定了一个$f$之后更新数组$A$和$B$。其中$A_i=\sum_{h_j\le i}f_j,B_i=\sum_{h_j\le i}1$。

哦对了如果$t_i=0$的话需要特判一下。。大概就是设这个高度有$p$个$t_i=0$的，那么

$$f_i=1+\frac{A_{h_i}+pf_i}{B_{h_i}+p}$$

其中$A_{h_i},B_{h_i}$都是不考虑这$p$个柱子得到的$A,B$。

解方程得到

$$f_i=1+\frac{p+A_{h_i}}{B_{h_i}}$$

复杂度：$O(n+h)$

然后这题卡常数，卡在哪儿呢?我们删去输出语句之后发现，只要220ms!所以我们使用手写的double输出过程就好啦！先输出整数部分再输出小数部分。

typedef long long int ll;
void pi(ll x){if (x > 9) pi(x / 10); putchar(x % 10 + 48);}
void putfloat(lf f){
  ll q = int(f * 100000) % 100000;
  pi(int(f)); putchar('.');
  if (q < 10000) putchar('0');
  if (q < 1000) putchar('0');
  if (q < 100) putchar('0');
  if (q < 10) putchar('0');
  pi(q);
} 

if (v(1,1) & 1){
  if (v(-1, -1) & 1){
    //do something
  } else {
    //do something
  }
} else {
  if (v(-1, -1) & 1){
    //do something
  } else {
    //do something
  }
}

清华集训2012 官方题解

清华集训2014 官方题解(11和13的找不到，TAT)

顾昱洲《Graphical Enumeration》

范浩强《从大象讲起——说说各种数据结构。》

https://en.wikipedia.org/wiki/Minkowski_addition

徐毅《浅谈回文子串问题》

许昊然《浅谈数据结构题的几个非经典解法》

hzaskywalker.blog.163.com/blog/static/2037981572013111244854169/

匡正非 黄志翱《两个冷门图论算法》

http://blog.sina.com.cn/s/blog_97a3fe860101er4g.html

陈立杰《计数问题选讲》

AC_Aerolight《专题讨论：计算几何与凸包算法》

http://jiruyi910387714.is-programmer.com/posts/74201.html

https://en.wikipedia.org/wiki/Set_cover_problem

https://en.wikipedia.org/wiki/Helly%27s_theorem