2011
【xor】
考虑做出一个生成树,每条非树边对应一个环,任意一个(每个点度数都是偶数的)子图都可以由这些环异或出来。
问题变成:给$m-n+1$个数$S$(环的xor值)和一个数$d$($s,t$在树上的xor距离),从$S$中选出一些使它们的xor和xor $d$最大。
高斯消元搞搞。
【joy】
首先对于一个$U$求出$D_\max$。我们发现:
1.$m$一定是$2$的倍数,别问我为什么。记$m=2k$。
2.答案等于$u_{i_2}-u_{i_1}+u_{i_4}-u_{i_3}+\dots +u_{i_m}-u_{i_{m-1}}$。而把$u$差分之后(差分后得到的数组记为$v$),这就是第$i_1+1\dots i_2$项,第$i_3+1\dots i_4$项,……,第$i_{m-1}+1\dots i_m$项之和。
如果要贪心选的话,首先$v_1$是选不到的,然后剩下的东西贪心吧,$>0$的就选,$<0$的就不选。由于题目说了最优下标序列唯一,所以差分后不会出现$=0$的玩意。
然后考虑第二问,就是假设最优序列选了$[l_1,r_1],[l_2,r_2],\dots,[l_k,r_k]$这个序列,然后小Y要扩充$i_{2k}=r_k,i_{2k+1}=l_{k+1}$,那么由于$(r_k,l_{k+1})$之间都是负数,所以最好尽量多选。但是又不能全选,那么显然是选除掉最大数以外的其他数。
我们维护一个平衡树,存储每一个负数块(移走$v$序列中的所有正数之后,$v$断裂成一些块)的权值(权值就是负数块的所有数的和减去其中最大数的和),然后支持询问权值绝对值前$k$大的块的权值和,套个二分(平衡树上的二分加询问可以$O(\log n)$而不是$O(\log^2 n)$)即可。
考虑修改操作,就是$v$数组的单点修改。第一问我就不说了→_→
首先我们用线段树维护每个点往左/右的第一个正/负数,以及rmq。
第二问的话分几种情况:
原来是负数,现在还是负数:更新一下负数块的权值。
原来是正数,现在还是正数:更新答案。
原来是负数,现在是正数:(+和-表示数的符号,红色的是将要变成正数的负数)
- +++-+++:删除这个负数块。
- +++----:更新这个负数块(----+++类似)。
- -------:删除这个负数块,加入两个新的负数块。
原来是整数,现在是负数:(同上)
- ---+---:合并两个负数块。
- ---++++:更新这个负数块(++++---类似)。
- +++++++:新建一个负数块。
注意后两种情况要更新答案。
然后就维护完啦~
p.s 数据有错,下面程序只有80分
http://www.lydsy.com/JudgeOnline/wttl/thread.php?tid=1884
#include <cstdio>
#include <cstdlib>
typedef long long int ll;
#define clr(x, k) for (int i = 0; i < k; i++) x[i] = 0;
template <class Q> void gi(Q &x){
char ch = getchar(); x = 0; bool s = 0;
while (ch < '0' || ch > '9'){if (ch == '-') s = 1; ch = getchar();}
while (ch >= '0' && ch <= '9') x = x * 10 + ch - 48, ch = getchar();
if (s) x = -x;
}
template <class Q> void pi(Q x){
if (x < 0){putchar('-'); pi(-x);}
else {if (x > 9) pi(x / 10); putchar(x % 10 + 48);}
}
const int sz = 100200;
int sta[sz], top, N;
int New(){if (N < 100000) return ++N; else return sta[top--];}
int rt, n;
int l[sz], r[sz], s[sz];
ll a[sz], sum[sz];
void S(int x){s[x] = s[l[x]] + s[r[x]] + 1; sum[x] = sum[l[x]] + sum[r[x]] + a[x];}
void L(int &x){int t = l[x]; l[x] = r[t]; r[t] = x; S(x); S(t); x = t;}
void R(int &x){int t = r[x]; r[x] = l[t]; l[t] = x; S(x); S(t); x = t;}
void mt(int &x){
if (s[l[l[x]]] > s[r[x]]){L(x); mt(l[x]); mt(x);}
if (s[r[r[x]]] > s[l[x]]){R(x); mt(r[x]); mt(x);}
if (s[l[r[x]]] > s[l[x]]){L(r[x]); R(x); mt(l[x]); mt(r[x]); mt(x);}
if (s[r[l[x]]] > s[r[x]]){R(l[x]); L(x); mt(l[x]); mt(r[x]); mt(x);}
}
void ins(int &t, int x){
if (t == 0){t = New(); a[t] = sum[t] = x; s[t] = 1; l[t] = r[t] = 0;}
else if (x < a[t]) ins(l[t], x); else ins(r[t], x);
S(t); mt(t);
}
void del(int &t, int x){
int i;
if (t == 0) return;
if (a[t] == x){
if (!l[t]){sta[++top] = t; t = r[t];}
else {
for (i = l[t]; r[i]; i = r[i]);
a[t] = a[i];
del(l[t], a[i]);
}
} else if (x < a[t]) del(l[t], x); else del(r[t], x);
if (t) {S(t); mt(t);}
}
int Query(int t, ll x){
if (sum[t] < x) return -1;
if (t == 0 || x <= 0) return 0;
if (sum[r[t]] >= x) return Query(r[t], x);
else return Query(l[t], x - sum[r[t]] - a[t]) + s[r[t]] + 1;
}
const int sn = 262200;
int T[sn], tn;
void _change(int x, int y){
T[x += tn] = y;
for (x >>= 1; x; x >>= 1) T[x] = T[x << 1] + T[x << 1 | 1];
}
int prev1(int x){
if (x < 2) return 1;
int s = tn, t = x + tn + 1;
for (; s ^ t ^ 1; s >>= 1, t >>= 1)
if ( t & 1) if (T[t ^ 1] != 0){t ^= 1; break;}
while (t <= tn){
if (T[t << 1 | 1]) t = t << 1 | 1;
else t = t << 1;
}
return t - tn;
}
int succ1(int x){
if (x > n) return n + 1;
int s = x + tn - 1, t = tn + tn + 2;
for (; s ^ t ^ 1; s >>= 1, t >>= 1)
if (~s & 1) if (T[s ^ 1] != 0){s ^= 1; break;}
while (s <= tn){
if (T[s << 1]) s <<= 1;
else s = s << 1 | 1;
}
return s - tn;
}
ll v[sz], MAX[sn], SUM[sn];
void Change(int x, int v2){
x += tn; MAX[x] = SUM[x] = v2;
for (x >>= 1; x; x >>= 1){
if (MAX[x << 1] > MAX[x << 1 | 1]) MAX[x] = MAX[x << 1]; else MAX[x] = MAX[x << 1 | 1];
SUM[x] = SUM[x << 1] + SUM[x << 1 | 1];
}
}
ll qsum(int l, int r){
ll ans = 0; int s = l + tn - 1, t = r + tn + 1;
for (; s ^ t ^ 1; s >>= 1, t >>= 1){
if (~s & 1) ans += SUM[s ^ 1];
if ( t & 1) ans += SUM[t ^ 1];
}
return ans;
}
ll qmax(int l, int r){
ll M = -1ll << 61; int s = l + tn - 1, t = r + tn + 1;
for (; s ^ t ^ 1; s >>= 1, t >>= 1){
if (~s & 1) if (M < MAX[s ^ 1]) M = MAX[s ^ 1];
if ( t & 1) if (M < MAX[t ^ 1]) M = MAX[t ^ 1];
}
return M;
}
ll value(int l, int r){
if (l == 2 || r == n) return 0;
return qmax(l, r) - qsum(l, r);
}
ll ans;
void change(int x, int v2){
int l, r, l1, r1, l2, r2;
if (v[x] > 0 && v2 > 0){
ans -= v[x]; v[x] = v2; ans += v[x];
} else if (v[x] <= 0 && v2 < 0){
l = prev1(x) + 1, r = succ1(x) - 1;
del(rt, value(l, r));
v[x] = v2;
Change(x, v2);
ins(rt, value(l, r));
} else if (v[x] <= 0 && v2 > 0){
l = prev1(x) + 1, r = succ1(x) - 1;
del(rt, value(l, r));
if (l <= x - 1) ins(rt, value(l, x - 1));
if (x + 1 <= r) ins(rt, value(x + 1, r));
_change(x, 1); v[x] = v2; ans += v[x];
} else {
l = prev1(x - 1) + 1, r = succ1(x + 1) - 1;
if (l <= x - 1) del(rt, value(l, x - 1));
if (x + 1 <= r) del(rt, value(x + 1, r));
_change(x, 0); ans -= v[x]; v[x] = v2;
Change(x, v2);
ins(rt, value(l, r));
}
Change(x, v2);
}
int q, u[sz];
void doit(){
int i, c;
clr(sta, top); clr(l, N); clr(r, N); clr(s, N); clr(sum, N); clr(a, N);
clr(T, tn + tn + 1); clr(MAX, tn + tn + 1); clr(SUM, tn + tn + 1);
clr(v, n + 10); rt = 0; top = 0; N = 0; ans = 0;
gi(n); gi(q);
for (i = 1; i <= n; i++) gi(u[i]);
for (i = 1; i <= n; i++) v[i] = u[i] - u[i - 1];
for (tn = 1; tn <= n + 3; tn <<= 1); tn--;
_change(1, 1); _change(n + 1, 1);
for (i = 2; i <= n; i++){
if (v[i] > 0) ans += v[i], _change(i, 1);
Change(i, v[i]);
}
int l, r;
for (l = 2; l <= n; )
if (v[l] < 0){
for (r = l; r <= n && v[r] < 0; r++);
ins(rt, value(l, r - 1));
l = r;
} else l++;
while (q--){
gi(i);
if (i == 1){
pi(ans), putchar(' ');
pi(Query(rt, ans)); putchar('\n');
} else {
gi(l); gi(r); gi(c); r++;
if (l >= 2) change(l, v[l] + c);
if (r <= n) change(r, v[r] - c);
}
}
}
int main(){
int T;
freopen("joy.in", "r", stdin); freopen("joy.out", "w", stdout);
gi(T);
while (T--) doit();
return 0;
}
【relation】
一道很好的提交答案题。
source等请跳至http://yunpan.cn/cdS7iRuPGSg5k (提取码:6f35)
很抱歉没有point 7~8的程序。。被误删了T_T
point 1
其实我并不会捉第一个点>_<
哪位神犇教教我吧
point 2~4
2是链,3,4是树。那就树形dp吧。为了输方案方便,转为二叉树。$f_{i,j}$表示选了$p_i$($i$原树上的父亲),从子树$i$中选$j$个点,那么$i$子树得到的最大收益(包括某个点与$p_i$之间的边);$g_{i,j}$表示没选$p_i$时的最大收益。
转移不说了>_<
(这种树p建议对拍)
point 5~6
point5是20*1500的二分图。。枚举左边选哪些,就可以知道右边每个点的收益,贪心选即可。
point6的话。。可以发现42的度数很大。。猜想它是个二分图(脑洞怎么这么大呀我完全想不到),发现是的,所以暴搜+贪心即可。
point6有多个连通块所以处理得很蛋疼。
point 7~8
据说补图是如point6一样的二分图,也是有一侧是20个点的那种。
这谁看得出来呀,还不如直接随机调整,可以调出理论最优解($\frac{k(k-1)}{2}$)。
point 9~10
据说求最大密度子图就可以了。
这谁看得出来呀,随机调整大法还只有15分。
乖乖写正解吧。
回忆一下最大密度子图:即最大化$\rho=w(E)/|V|$。现在考虑二分答案$\rho$然后判断是否存在一个子图它的$w(E)>\rho|V|$。即每个点有代价每条边有收益选择两个点才能选择对应边所以转化为最大权闭合图用最小割做一做就可以了>_<
精度比较烦人,二分出$\rho$之后最好减个$1$再求最大权闭合图。(权值比较大,减$10^{-6}$效果不好,减$1$不会错)
(hbt的论文上有更优复杂度的做法哦)
2012
【mst】
见范爷博客
http://fanhq666.blog.163.com/blog/static/8194342620121185107104/
考虑kruskal过程中,同时处理权值相同的边。扔掉没用(小于它的权值构成的边能将它的两点联通)的边,剩下的边中进行一系列-1和+1,支付相应费用并使其变成一棵树。-1就是缩点,+1就是删除。
设剩下$m$条该权值的边,连接出了$k$个连通块,$m$条边涉及的点共有$n$个。
如果只准+1,那么答案就是$m+k-n$。
如果只准-1,那么答案就是(每个双连通块的大小减一)之和。
否则暴力。桥是可以无视的,然后每个双连通块暴搜。下发的数据中point10可以手算,其他数据的双连通分量大小都不超过12。我们考虑怎么暴力。现在我们的问题变成:给一个双连通图,求答案。假设我们先执行所有缩点操作之后,得到一个并查集,$d_i$表示$i$所在集合的代表元$(d_i\le i)$。然后删边直到是一棵树为止。缩点代价为$a$,删边代价为$b$。首先我们枚举这个并查集,然后要缩点的次数就是$d_i\neq i$的个数;删掉的边数就是$d_i\neq d_j$的边(当然要留下一些边组成一棵生成树,连接所有集合)。
枚举$d$数组,枚举量是$O(n!)$的,$n$是双连通块的大小。
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
void gi(int &x){char ch = getchar(); x = 0; while (ch < '0' || ch > '9') ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - 48, ch = getchar();}
int n, m, a, b;
pair <int, pair <int, int> > E[1002000];
int dsu[500200];
int find(int x){return x == dsu[x] ? x : dsu[x] = find(dsu[x]);}
#define fi first
#define se second
int ANS = 0;
namespace Graph{
const int sz = 1002000;
int node[sz], next[sz], to[sz], e, X[sz], c, u[sz], c2;
void ens(int x, int y){
e++; next[e] = node[x]; node[x] = e; to[e] = y;
if (!u[x]){X[++c] = x; u[x] = 1;}
}
void bis(int x, int y){ens(x, y); ens(y, x);}
int dfn[sz], low[sz], ins[sz], vis[sz], sta[sz], in[sz];
int bb[52], cc;
int top, Dfn, tot;
void clr(){
int i, p;
for (i = 1; i <= c; i++){
p = X[i]; node[p] = 0; X[i] = 0; u[p] = 0;
dfn[p] = low[p] = ins[p] = vis[p] = sta[p] = 0;
}
c = e = top = Dfn = 0;
}
void tarjan(int x, int J){
int j, cc = 0;
Dfn++; dfn[x] = low[x] = Dfn; ins[x] = vis[x] = 1; sta[++top] = x;
for (j = node[x]; j; j = next[j])
if (ins[to[j]] && j != (J & 1 ? J + 1 : J - 1)){
if (dfn[to[j]] < low[x]) low[x] = dfn[to[j]];
} else if (!vis[to[j]]){
tarjan(to[j], j);
if (low[to[j]] < low[x]) low[x] = low[to[j]];
}
if (low[x] == dfn[x]){
do{j = sta[top--]; cc++;} while (j != x);
if (a == 1) ANS += cc - 1;
}
}
};
int main(){
int i, j, x, y, ec;
freopen("mst.in", "r", stdin); freopen("mst.out", "w", stdout);
gi(i);
gi(n); gi(m); gi(a); gi(b);
for (i = 1; i <= m; i++) gi(E[i].se.fi), gi(E[i].se.se), gi(E[i].fi);
sort(E + 1, E + m + 1);
for (i = 1; i <= n; i++) dsu[i] = i;
for (i = 1; i <= m; ){
Graph::clr(); ec = 0;
for (j = i; j <= m && E[j].fi == E[i].fi; j++)
if (find(E[j].se.fi) != find(E[j].se.se))
Graph::bis(find(E[j].se.fi), find(E[j].se.se)), ec++;
y = 0;
for (j = 1; j <= Graph::c; j++){
x = Graph::X[j];
if (!Graph::vis[x]){
Graph::tarjan(x, 1000000000);
y++;
}
}
if (b == 1) ANS += ec - Graph::c + y;
for (j = i; j <= m && E[j].fi == E[i].fi; j++)
dsu[find(E[j].se.fi)] = find(E[j].se.se);
i = j;
}
printf("%d\n", ANS);
return 0;
}
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
void gi(int &x){char ch = getchar(); x = 0; while (ch < '0' || ch > '9') ch = getchar(); while (ch >= '0' && ch <= '9') x = x * 10 + ch - 48, ch = getchar();}
int n, m, a, b;
pair <int, pair <int, int> > E[1002000];
int dsu[500200];
int find(int x){return x == dsu[x] ? x : dsu[x] = find(dsu[x]);}
#define fi first
#define se second
namespace BCG{
int N, A = 1000000000;
int d[52];
int mm[52][52];
void clr(){
int i, j; A = 1000000000;
for (i = 1; i <= N; i++)
for (j = i + 1; j <= N; j++)
mm[i][j] = 0;
N = 0;
}
int check(){
int i, j, ans = 0;
for (i = 1; i <= N; i++)
if (d[i] != i) ans += a + b;
for (i = 1; i <= N; i++)
for (j = i + 1; j <= N; j++)
if (d[i] != d[j]) ans += mm[i][j] * b;
ans -= (N - 1) * b;
return ans;
}
void dfs(int x){
if (x == N + 1){
int q = check();
if (q < A) A = q;
} else {
for (d[x] = 1; d[x] <= x; d[x]++)
if (d[d[x]] == d[x])
dfs(x + 1);
}
}
};
namespace Graph{
const int sz = 1002000;
int node[sz], next[sz], to[sz], e, X[sz], c, u[sz], c2;
void ens(int x, int y){
e++; next[e] = node[x]; node[x] = e; to[e] = y;
if (!u[x]){X[++c] = x; u[x] = 1;}
}
void bis(int x, int y){ens(x, y); ens(y, x);}
int dfn[sz], low[sz], ins[sz], vis[sz], sta[sz], in[sz];
int bb[52], cc;
int top, Dfn, ANS = 0;
void clr(){
int i, p;
for (i = 1; i <= c; i++){
p = X[i]; node[p] = 0; X[i] = 0; u[p] = 0;
dfn[p] = low[p] = ins[p] = vis[p] = sta[p] = 0;
}
c = e = top = Dfn = ANS = 0;
}
void tarjan(int x, int J){
int j;
Dfn++; dfn[x] = low[x] = Dfn; ins[x] = vis[x] = 1; sta[++top] = x;
for (j = node[x]; j; j = next[j])
if (ins[to[j]] && j != (J & 1 ? J + 1 : J - 1)){
if (dfn[to[j]] < low[x]) low[x] = dfn[to[j]];
} else if (!vis[to[j]]){
tarjan(to[j], j);
if (low[to[j]] < low[x]) low[x] = low[to[j]];
}
if (low[x] == dfn[x]){
cc = 0; BCG::clr();
do {
j = sta[top--]; bb[++cc] = j; in[j] = cc;
} while (j != x);
BCG::N = cc;
for (int i = 1; i <= cc; i++)
for (j = node[bb[i]]; j; j = next[j])
if (in[to[j]])
BCG::mm[i][in[to[j]]]++;
BCG::dfs(1);
ANS += BCG::A;
for (j = 1; j <= cc; j++) in[bb[j]] = 0;
c2 -= cc; cc = 0;
fprintf(stderr, "%d\n", c2);
}
}
};
int main(){
int i, j, x, ANS = 0;
freopen("mst9.in", "r", stdin); freopen("mst.out", "w", stdout);
gi(i);
gi(n); gi(m); gi(a); gi(b);
for (i = 1; i <= m; i++) gi(E[i].se.fi), gi(E[i].se.se), gi(E[i].fi);
sort(E + 1, E + m + 1);
for (i = 1; i <= n; i++) dsu[i] = i;
for (i = 1; i <= m; ){
fprintf(stderr, "%d\n", i);
Graph::clr();
for (j = i; j <= m && E[j].fi == E[i].fi; j++)
if (find(E[j].se.fi) != find(E[j].se.se))
Graph::bis(find(E[j].se.fi), find(E[j].se.se));
Graph::c2 = Graph::c;
for (j = 1; j <= Graph::c; j++){
x = Graph::X[j];
if (!Graph::vis[x]) Graph::tarjan(x, 1000000000);
}
ANS += Graph::ANS;
for (j = i; j <= m && E[j].fi == E[i].fi; j++)
dsu[find(E[j].se.fi)] = find(E[j].se.se);
i = j;
}
printf("%d\n", ANS);
return 0;
}
【memory】
又是江苏省常州市高级中学will出的神题
考虑只准往上走的情况,对每两条线段$a,b$,如果移走$a$之前必须移走$b$那么连边$a\to b$。考虑如何减小连边数。
边$a\to b$的充要条件是存在$x=x_0$与两条线段都相交,且与$b$的交点更靠上。然后所有的$x_0$我们只需要扫描线段端点(就是题面中的$a_i$和$c_i$),只有在某条扫描线中相邻的两条线段才有必要连边。而对于扫描线我们需要做的就是插入一个点($a_i$)和删除一个点($c_i$),每一个事件只需要连接$O(1)$条边,事件的个数是$O(n)$。
这样就建出了dag。通过这个dag的拓扑排序我们可以得到第二问的答案。
第一问?如果只有往上走那么我们当然可以在每删除一个点的时候判一下合法。现在有四个方向,我们做四个dag出来,每往一个方向走我们就在每个dag中都删除一个点。
好像就可以~\(≧▽≦)/~啦啦啦
同学请问你代码中的LXK是什么意思
#include <cstdio>
#include <set>
#include <algorithm>
using namespace std;
#define sz 102020
#define fi first
#define se second
#define mp make_pair
#define pii pair <int, int>
int n;
class LXK{
public:
int a[sz], b[sz], c[sz], d[sz], i;
pair <pii, pii> lxk[sz << 1];
double calcy(int x, int e){
return double(d[e] - b[e]) * double(x - a[e]) / double(c[e] - a[e]) + b[e];
}
set <pii> ec;
#define mp4(a, b, c, d) mp(mp(a, b), mp(c, d))
int node[sz], next[sz << 2], to[sz << 2];
int deg[sz], e;
int l[sz], r[sz], A[sz], s[sz], N, rt;
void S(int x){s[x] = s[l[x]] + s[r[x]] + 1;}
void L(int &x){int t = l[x]; l[x] = r[t]; r[t] = x; S(x); S(t); x = t;}
void R(int &x){int t = r[x]; r[x] = l[t]; l[t] = x; S(x); S(t); x = t;}
void mt(int &x){
if (s[l[l[x]]] > s[r[x]]){L(x); mt(l[x]); mt(x);}
if (s[r[r[x]]] > s[l[x]]){R(x); mt(r[x]); mt(x);}
if (s[l[r[x]]] > s[l[x]]){L(r[x]); R(x); mt(l[x]); mt(r[x]); mt(x);}
if (s[r[l[x]]] > s[r[x]]){R(l[x]); L(x); mt(l[x]); mt(r[x]); mt(x);}
}
void inse(int &t, int x){
if (t == 0){t = ++N; A[t] = x; s[t] = 1; l[t] = r[t] = 0;}
else if (calcy(lxk[i].fi.fi, x) < calcy(lxk[i].fi.fi, A[t]))
inse(l[t], x); else inse(r[t], x);
S(t); mt(t);
}
void del(int &t, int x){
if (x == A[t]){
int i;
if (r[t] == 0) t = l[t];
else {
for (i = r[t]; l[i]; i = l[i]);
A[t] = A[i]; del(r[t], A[i]);
}
} else if (calcy(lxk[i].fi.fi, x) < calcy(lxk[i].fi.fi, A[t]))
del(l[t], x); else del(r[t], x);
if (t) S(t), mt(t);
}
int select(int t, int k){
if (k == s[l[t]] + 1) return A[t];
else if (k <= s[l[t]]) return select(l[t], k);
else return select(r[t], k - s[l[t]] - 1);
}
int rank(int t, int x){
if (t == 0) return 0;
if (calcy(lxk[i].fi.fi, x) < calcy(lxk[i].fi.fi, A[t]))
return rank(l[t], x);
else return rank(r[t], x) + s[l[t]] + 1;
}
//high -> low
void ins(int x, int y){
if (ec.find(mp(x, y)) != ec.end()) return; ec.insert(mp(x, y));
e++; next[e] = node[x]; node[x] = e; to[e] = y; deg[y]++;
}
int cdeg[sz];
void crdag(){
int j, k = 0, x, y, U, D, sjx, sjb;
for (i = 1; i <= n; i++){
if (a[i] > c[i]) swap(a[i], c[i]), swap(b[i], d[i]);
k++; lxk[k] = mp4(a[i], 1, b[i], i);
k++; lxk[k] = mp4(c[i], -1, d[i], i);
}
sort(lxk + 1, lxk + k + 1);
for (i = 1; i <= k; i++){
x = lxk[i].fi.fi; y = lxk[i].se.fi; j = lxk[i].se.se;
sjb = rank(rt, j);
if (lxk[i].fi.se == 1){
if (sjb != s[rt]) ins(select(rt, sjb + 1), j);
if (sjb != 0) ins(j, select(rt, sjb));
inse(rt, j);
} else {
del(rt, j);
sjb = rank(rt, j);
if (sjb != s[rt] && sjb != 0)
ins(select(rt, sjb + 1), select(rt, sjb));
}
}
for (i = 1; i <= n; i++) cdeg[i] = deg[i];
}
int q[sz];
void topsort(){
int i, j, k, l = 1, r = 0;
for (i = 1; i <= n; i++){
if (cdeg[i] == 0) q[++r] = i;
}
while (l <= r){
k = q[l++];
for (j = node[k]; j; j = next[j]){
cdeg[to[j]]--;
if (cdeg[to[j]] == 0) q[++r] = to[j];
}
printf("%d 1\n", k);
}
}
void delnode(int x){
int i;
for (i = node[x]; i; i = next[i]) deg[to[i]]--;
}
} yjy[4];
int a[sz], b[sz], c[sz], d[sz];
int main(){
int i, j, k, l;
freopen("memory.in", "r", stdin); freopen("memory.out", "w", stdout);
scanf("%d", &n);
for (i = 1; i <= n; i++){
scanf("%d %d %d %d", a + i, b + i, c + i, d + i);
yjy[0].a[i] = b[i]; yjy[0].b[i] = -a[i]; yjy[0].c[i] = d[i]; yjy[0].d[i] = -c[i];
yjy[1].a[i] = a[i]; yjy[1].b[i] = b[i]; yjy[1].c[i] = c[i]; yjy[1].d[i] = d[i];
yjy[2].a[i] = b[i]; yjy[2].b[i] = a[i]; yjy[2].c[i] = d[i]; yjy[2].d[i] = c[i];
yjy[3].a[i] = a[i]; yjy[3].b[i] = -b[i]; yjy[3].c[i] = c[i]; yjy[3].d[i] = -d[i];
}
for (i = 0; i < 4; i++) yjy[i].crdag();
for (i = 1; i <= n; i++){
scanf("%d %d", &j, &k);
if (yjy[k].deg[j] != 0){
printf("%d\n", i);
break;
}
for (k = 0; k < 4; k++)
yjy[k].delnode(j);
}
yjy[1].topsort();
return 0;
}
【catan】
写个模拟器,然后手玩。
2013
【graph】
1.平面图转对偶图
这个没什么难度吧。算法就是找一个一个的域。可以最先找禁区,把禁区标为0或1。把每条无向边\((u,v)\)拆成两条有向边\((u,v)\)和\((v,u)\)。我们要求的就是,对于每条有向边\((u,v)\),我站在\(u\)点望着\(v\)点,右手边的区域。
对每条没有被遍历过的边\((u,v)\),我们从\(u\)走到\(v\),然后站在\(v\)点望着\(u\)点。此时我们向左转,转到第一次与另一条边重合时(这个用set维护一下即可),就走这条边。这样可以得到所有的域(包括禁区)。如图:
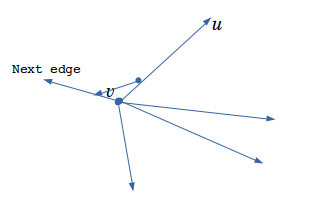
向左转。
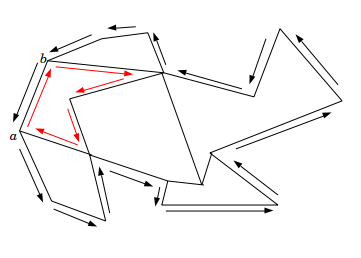
如果第一条边从\(b\)到\(a\),那么求的是禁区;如果第一条边从\(a\)到\(b\),那么求的是红色边包围的域。
2.点定位
离线扫描线。把所有点都排序。然后扫描线。
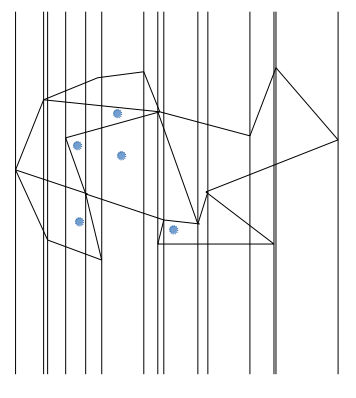
如图。扫描线把平面图分成了一堆条形区域。在条形区域内询问点在哪个地方显然更容易些。
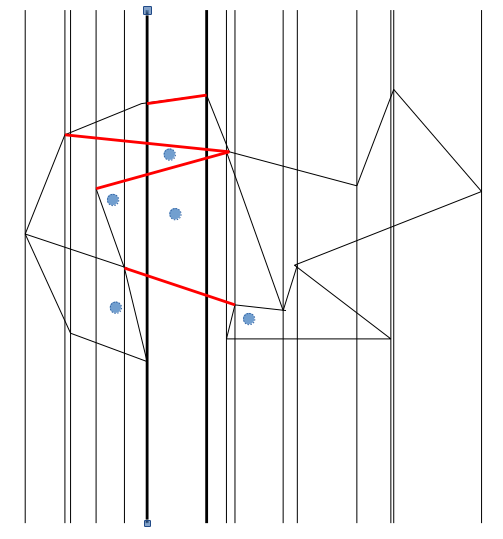
如果扫描到上图中粗黑线之间的部分,就把所有红色的线段(有向线段,方向从左到右。所有竖直线段我们都不用操心)加入一棵平衡树。注意到红色线段肯定不会在端点外相交,所以它们是可排序的。然后在平衡树中找出每个询问点上面的第一条线段,它所属的域就是询问点所属的域。

当扫描线变动的时候,设第\(x-1\)条扫描线被删掉,第\(x+1\)条扫描线加入。那么扫描第\(x-1\)条线上的所有点\(u\),在平衡树中删掉所有\(u\)往右连的边。然后扫描第\(x\)条线上的所有点,加入它们往右连的所有边。注意一定要先删除再加入,否则平衡树的可排序性质将被打乱。比如上图删除蓝色线段再加入紫色线段,三条红色的线段不用管。
3.回答每个询问
在对偶图的最小生成树上做即可。注意对偶图可能不连通。
其实写的时候没什么感觉,写完了之后已经7k+了。加了几个补丁之后就8.6K了。代码。
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <set>
#define sz 200200
#define huge (1 << 30)
#define hugell (1ll << 60)
#define hugef 1e40
#define eps 1e-10
inline int Pair(int x){return((x & 1) ? x + 1 : x - 1);}
typedef double lf;
typedef long long int ll;
using namespace std;
class point{
public:
ll x, y;
point(){x = y = 0;}
point(ll a, ll b){x = a; y = b;}
};
typedef point vector;
point operator + (point p, point q){return point(p.x + q.x, p.y + q.y);}
point operator - (point p, point q){return point(p.x - q.x, p.y - q.y);}
point operator * (point p, lf q){return point(p.x * q, p.y * q);}
ll dot(vector u, vector v){return u.x * v.x + u.y * v.y;}
ll det(vector u, vector v){return u.x * v.y - v.x * u.y;}
point P[sz];
ll node[sz], next[sz], to[sz], E[sz][3], bel[sz], yu[sz];
class edge{
public:
ll from, to, bh;
lf ang;
edge(){}
edge(ll f, ll t){to = t; from = f; ang = atan2(P[to].y - P[from].y, P[to].x - P[from].x);}
edge(ll f, ll t, ll b){to = t; from = f; ang = atan2(P[to].y - P[from].y, P[to].x - P[from].x); bh = b;}
};
bool operator < (edge a, edge b){return a.ang < b.ang;}
edge turn_left(set <edge> &S, edge get){
set <edge> :: iterator j = S.upper_bound(edge(get.to, get.from));
if (j == S.end()) return *S.begin();
else return *j;
}
set <edge> S[sz];
point Q[sz * 2];
ll a[sz];
ll n, m, q, e;
void ins(ll x, ll y){
e++; next[e] = node[x]; node[x] = e; to[e] = y;
S[x].insert(edge(x, y, e));
}
void __sw(ll x, ll y){
ll t;
t = Q[x].x; Q[x].x = Q[y].x; Q[y].x = t;
t = Q[x].y; Q[x].y = Q[y].y; Q[y].y = t;
t = a[x]; a[x] = a[y]; a[y] = t;
}
void qsort(ll l, ll r){
ll i = l, j = r, mid = Q[rand() % (r - l) + l].x;
while (i <= j){
for (; Q[i].x < mid; i++);
for (; Q[j].x > mid; j--);
if (i <= j) __sw(i++, j--);
}
if (l < j) qsort(l, j); if (i < r) qsort(i, r);
}
void gf(ll &x){
double tmp;
ll tm2;
scanf("%lf", &tmp); tm2 = (ll)tmp;
if (tmp - tm2 > 0.3) x = tm2 * 2 + 1;
else x = tm2 * 2;
}
void gi(ll &x){
char ch = getchar(); x = 0;
while (ch < '0' || ch > '9') ch = getchar();
while (ch >= '0' && ch <= '9') x = x * 10 + ch - 48, ch = getchar();
}
void init(){
ll i, x, y, z, j;
freopen("graph.in", "r", stdin); freopen("graph.out", "w", stdout);
gi(n); gi(m);
for (i = 1; i <= n; i++){
gi(P[i].x); gi(P[i].y);
P[i].x *= 2; P[i].y *= 2;
}
for (i = 1; i <= m; i++){
gi(x); gi(y); gi(z);
E[i][0] = x; E[i][1] = y; E[i][2] = z;
ins(x, y); ins(y, x);
}
gi(q);
for (i = 0; i < q; i++){
gf(Q[i << 1].x); gf(Q[i << 1].y);
a[i << 1] = i << 1;
gf(Q[i << 1 | 1].x); gf(Q[i << 1 | 1].y);
a[i << 1 | 1] = i << 1 | 1;
}
qsort(0, (q << 1) - 1);
}
ll cnt;
void getyu(edge e){
ll i = e.from; cnt++;
for (; e.to != i; e = turn_left(S[e.to], e)) yu[e.bh] = cnt;
yu[e.bh] = cnt;
}
void getall(){
ll i, j, k;
//1 is the forbid.
cnt = 0; j = 1;
for (i = 2; i <= n; i++) if (P[i].x < P[j].x) j = i;
k = node[j];
for (i = next[k]; i; i = next[i])
if ((P[to[i]].y - P[j].y) * (P[to[k]].x - P[j].x) < (P[to[k]].y - P[j].y) * (P[to[i]].x - P[j].x))
k = i;
getyu(edge(j, to[k], k));
for (i = 1; i <= n; i++)
for (j = node[i]; j; j = next[j])
if (!yu[j]) getyu(edge(i, to[j], j));
}
int up(point p1, point p2, point p3, point p4, int x){
double x1 = p1.y + (x - p1.x) * (p2.y - p1.y) / (double)(p2.x - p1.x);
double x2 = p3.y + (x - p3.x) * (p4.y - p3.y) / (double)(p4.x - p3.x);
return x1 > x2 * (1 + eps);
}
class SBT{
public:
ll l[sz], r[sz], s[sz], a[sz];
point A[sz], B[sz];
ll n;
void S(ll x){s[x] = s[l[x]] + s[r[x]] + 1;}
void L(ll &x){ll t = l[x]; l[x] = r[t]; r[t] = x; S(x); S(t); x = t;}
void R(ll &x){ll t = r[x]; r[x] = l[t]; l[t] = x; S(x); S(t); x = t;}
void mt(ll &x){
if (s[l[l[x]]] > s[r[x]]){L(x); mt(l[x]); mt(x);}
if (s[r[r[x]]] > s[l[x]]){R(x); mt(r[x]); mt(x);}
if (s[l[r[x]]] > s[l[x]]){L(r[x]); R(x); mt(l[x]); mt(r[x]); mt(x);}
if (s[r[l[x]]] > s[r[x]]){R(l[x]); L(x); mt(l[x]); mt(r[x]); mt(x);}
}
void ins(ll &t, ll x, ll le, ll ri){
if (t == 0){
t = ++n; l[t] = r[t] = 0; s[t] = 1; A[t] = P[to[Pair(x)]]; B[t] = P[to[x]]; a[t] = x;
if (B[t].x < A[t].x) swap(A[t], B[t]);
} else if (up(A[t], B[t], P[to[x]], P[to[Pair(x)]], le) || up(A[t], B[t], P[to[x]], P[to[Pair(x)]], ri)) ins(l[t], x, le, ri);
else ins(r[t], x, le, ri);
S(t); mt(t);
}
void del(ll &t, ll x, ll le, ll ri){
if (a[t] == x){
ll i;
if (!l[t]) t = r[t];
else{
for (i = l[t]; r[i]; i = r[i]);
A[t] = A[i]; B[t] = B[i]; a[t] = a[i];
del(l[t], a[i], le, ri);
}
} else if (up(A[t], B[t], P[to[x]], P[to[Pair(x)]], le) || up(A[t], B[t], P[to[x]], P[to[Pair(x)]], ri)) del(l[t], x, le, ri);
else del(r[t], x, le, ri);
if (t) {S(t); mt(t);}
}
ll query(ll t, ll x, ll y){
ll i;
if (t == 0) return -1;
if ((x - A[t].x) * (B[t].y - A[t].y) + A[t].y * (B[t].x - A[t].x) > y * (B[t].x - A[t].x)){
i = query(l[t], x, y);
if (i == -1) return a[t]; else return i;
} else return query(r[t], x, y);
}
} T_T;
ll qy[sz];
ll A[sz];
void Qsort(ll l, ll r){
ll i = l, j = r, mid = P[A[rand() % (r - l) + l]].x;
while (i <= j){
for (; P[A[i]].x < mid; i++);
for (; P[A[j]].x > mid; j--);
if (i <= j){ll t = A[i]; A[i] = A[j]; A[j] = t; i++; j--;}
}
if (l < j) Qsort(l, j); if (i < r) Qsort(i, r);
}
void ddw(){
ll i, j, k, l = 0, rt = 0, le, ri;
for (i = 1; i <= n; i++) A[i] = i;
if (n > 1) Qsort(1, n);
for (i = 0; i < q + q; i++) bel[i] = 1;
for (; Q[l].x <= P[A[1]].x; l++);
for (i = 1; i <= n; i = j){
for (j = i; P[A[j]].x == P[A[i]].x; j++)
for (k = node[A[j]]; k; k = next[k])
if (P[to[k]].x < P[A[j]].x) T_T.del(rt, Pair(k), le, ri);
le = P[A[i]].x;
for (j = i; P[A[j]].x == P[A[i]].x; j++);
ri = P[A[j]].x; if (j > n) break;
for (j = i; P[A[j]].x == P[A[i]].x; j++)
for (k = node[A[j]]; k; k = next[k])
if (P[to[k]].x > P[A[j]].x) T_T.ins(rt, k, le, ri);
for (; l < q + q && Q[l].x <= P[A[j]].x; l++){
ll tmp = T_T.query(rt, Q[l].x, Q[l].y);
bel[l] = (tmp == -1 ? 1 : yu[tmp]);
}
}
}
class stupid{
public:
ll node[sz], next[sz], to[sz], w[sz], dsu[sz];
ll e, ed[sz][3], mm;
stupid(){mm = 0;}
void ins(ll x, ll y, ll v){e++; next[e] = node[x]; node[x] = e; to[e] = y; w[e] = v;}
ll find(ll x){return x == dsu[x] ? x : dsu[x] = find(dsu[x]);}
void swaq(ll i, ll j){
ll x;
x = ed[i][0]; ed[i][0] = ed[j][0]; ed[j][0] = x;
x = ed[i][1]; ed[i][1] = ed[j][1]; ed[j][1] = x;
x = ed[i][2]; ed[i][2] = ed[j][2]; ed[j][2] = x;
}
void qsorT(ll l, ll r){
ll i = l, j = r, mid = ed[rand() % (r - l) + l][2];
while (i <= j){
for (; ed[i][2] < mid; i++);
for (; ed[j][2] > mid; j--);
if (i <= j) swaq(i++, j--);
}
if (l < j) qsorT(l, j); if (i < r) qsorT(i, r);
}
void init(){
ll i;
for (i = 1; i <= m; i++)
if (yu[(i - 1) << 1 | 1] != 1 && yu[i << 1] != 1){
ed[++mm][0] = yu[(i - 1) << 1 | 1];
ed[mm][1] = yu[i << 1];
ed[mm][2] = E[i][2];
}
if (mm > 1) qsorT(1, mm);
for (i = 2; i <= cnt; i++) dsu[i] = i;
for (i = 1; i <= mm; i++)
if (find(ed[i][0]) != find(ed[i][1])){
dsu[dsu[ed[i][0]]] = dsu[ed[i][1]];
ins(ed[i][0], ed[i][1], ed[i][2]);
ins(ed[i][1], ed[i][0], ed[i][2]);
}
}
ll q[sz], f[sz][30], g[sz][30], dep[sz];
void bfs(ll bg){
ll i, j, k, l, r;
q[l = r = 0] = bg; dep[bg] = 1;
while (l <= r){
k = q[l++];
for (j = node[k]; j; j = next[j])
if (to[j] != f[k][0]){
q[++r] = to[j];
dep[to[j]] = dep[k] + 1;
f[to[j]][0] = k;
g[to[j]][0] = w[j];
}
}
}
void bfs(){
ll i;
for (i = 2; i <= cnt; i++) if (dep[i] == 0) bfs(i);
}
void bz(){
ll i, j;
for (j = 1; j < 20; j++)
for (i = 2; i <= cnt; i++){
f[i][j] = f[f[i][j - 1]][j - 1];
g[i][j] = max(g[f[i][j - 1]][j - 1], g[i][j - 1]);
}
}
ll query(ll x, ll y){
ll d = dep[x] - dep[y], j, a = 0;
if (x == 1 || y == 1) return -1;
if (d < 0){
d = -d;
x ^= y; y ^= x; x ^= y;
}
for (j = 0; d; d >>= 1, j++)
if (d & 1){
a = max(a, g[x][j]);
x = f[x][j];
}
if (x == y) return a;
for (j = 19; j >= 0; j--)
if (f[x][j] != f[y][j]){
a = max(a, max(g[x][j], g[y][j]));
x = f[x][j]; y = f[y][j];
}
if (f[x][0] == 0) return -1;
return max(a, max(g[x][0], g[y][0]));
}
} r_64;
ll b[sz];
int main(){
ll i;
init();
getall();
ddw();
for (i = 0; i < q + q; i++) b[a[i]] = i;
r_64.init(); r_64.bfs(); r_64.bz();
for (i = 0; i < q; i++) printf("%lld\n", r_64.query(bel[b[i << 1]], bel[b[i << 1 | 1]]));
return 0;
}
【park】
莫队算法。。常数被虐成狗。。(树分块太神辣不会)
假设我们知道询问\((x_1,y_1,t_1)\)的答案,也就是\(t_1\)时刻有一个询问\(x_1,y_1\)。我们想求询问\((x_2,y_2,t_2)\)的答案。这里假设\(t_2>t_1\)。
那么我们把点\(x_1\)暴力移到\(x_2\)。同时给每条边记录一个值,表示它是否在路径\((x,y)\)上。初始时\(x=x_1,y=y_1\),在移动的过程中会有变化,到最后\(x=x_2,y=y_2\)。每当我们把\(x\)从\(x_u\)移到了\(x_v\),那么边\((x_u,x_v)\)的状态(在不在路径上)取反。再按照同样的方法移\(y\)。处理边的时候,如果某个端点连出去的所有边突然都不在路径上了(给点记录一个值即可),或者连出去的某条边在路径上了,就拿这个点更新一下答案。
于是我们成功地从\((x_1,y_1)\)的状态转化到了\((x_2,y_2)\)的状态。
关于\(t\)嘛。。先把\(t_1\)到\(t_2\)之间的修改都做完了,就可以直接转了。
设点\(x\)在DFS序中的位置是\(pos_x\)。那么一次转移的时间复杂度是
\(O(|pos_{x_1}-pos_{x_1}|+|pos_{x_2}-pos_{y_2}|+t_2-t_1)\)。
于是可以用经典的莫队算法这类东西做。
设一个常数\(S\),把询问\(x,y\)按照\((\lfloor\frac{x}{S}\rfloor,\lfloor\frac{y}{S}\rfloor)\)分类,每一类的询问按照时间排序。每处理一类的时间复杂度就是\(O(q\frac{n}{S}+Q)\),其中\(q\)是这一类的询问个数,\(Q\)是总询问个数。那么总复杂度就是\(O(Q(S^2+\frac{n}{S}))\)。取\(S=n^{\frac{1}{3}}\),得到复杂度\(O(Qn^{\frac{2}{3}})\)。
【sports】
傻逼360云盘失效了。。点我
2014
【space】
傻逼360云盘失效了。。点我
【flower】
考虑树的形态固定的时候,点分治显然可以求答案。加入一个点的时候用替罪羊树一样的方法维护点分治即可。
【nm】
nm是很好玩的提交答案题。
1:算法0。根据样例可以看出是邻接矩阵。
#include <cstdio>
int n;
int main(){
freopen("nm1.in", "r", stdin); freopen("nm1.out", "w", stdout);
scanf("%d 0 0\n", &n);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++){
int k;
scanf("%d", &k);
if (k == 1) printf("%d %d 1\n", i, j);
}
return 0;
}
2:算法10。发现是单源最短路。但是边权不能超过20000很蛋疼。
一个很简单的构造方法:取\(i=1\),对\(d_j>d_i\)且\(d_j \le d_i+20000\)的点连一条边\(i,j,d_j-d_i\)。再将\(i\)置为上述\(j\)中\(d_j\)最大的,重复下去,直到所有边都连了为止。于是我们构出了一棵树,再补\(10001\)条边即可。取一些不连出边的点\(x\),向每一个满足\(d_x+20000>d_y\)的点\(y\)连一条长度为\(20000\)的边。直到连够了边为止。
#include <cstdio>
int d[23456];
int main(){
int i, j, k, sc = 0;
freopen("nm2.in", "r", stdin); freopen("nm2.out", "w", stdout);
scanf("%*d %*d %*d");
for (i = 1; i <= 10000; i++) scanf("%d", &d[i]);
j = 1;
for (int x = 1; x <= 6; x++){
k = j;
for (i = 1; i <= 10000; i++)
if (d[i] > d[j] && d[i] <= d[j] + 20000){
if (d[i] > d[k]) k = i;
printf("%d %d %d\n", j, i, d[i] - d[j]), sc++;
}
j = k;
}
i = 2;
while (sc < 20000){
for (j = 1; j <= 10000; j++)
if (d[j] < d[i] + 20000){
printf("%d %d %d\n", i, j, 20000);
sc++; if (sc == 20000) break;
}
i++;
}
return 0;
}
3.算法11。再看数据规模猜测是所有点之间的最短路。拿程序1直接跑即可(矩阵中为1的那些值恰好就是一条边)。
4.算法12。次短路。试了几遍之后发现点1的次短路是经过点1的最短环的长度。于是开始构造。考虑一个“装置”,它能使次短路比最短路长\(18000\)。这个装置就是一个点,1号点向它连边,它向1号点的其他出边所指的点连边。只要保证经过这个点的路径长度增加\(18000\)即可。然后就可以像算法10一样地构树了。同时,设1号到树上另一个点的最短路为\(x\),那么连一条边长度为\(92752-x\),其中92752是一号点到自己的次短路长。这样就可以解决问题了。另外,装置中的点的次短路是92752+1号到它的距离。装置的话。。。选\(d\)最大的点吧。不然那个点到 1号点的出边所指的点 的距离可能超过20000。
#include <cstdio>
int d[10202], v[10202], q[10202];
int i, j, k, n = 10000, m = 0, P = 379;
int main(){
freopen("nm4.in", "r", stdin); freopen("nm4.out", "w", stdout);
scanf("%*d %*d %*d");
for (i = 1; i <= n; i++){scanf("%d", &d[i]); if (d[i] == 112374) P = i;}
for (i = 2; i <= n; i++)
if (i != P) d[i] -= 18000;
int tmp = d[1];
j = 1; d[1] = 0;
for (int x = 1; x <= 6; x++){
k = j; q[j] = 1;
for (i = 1; i <= 10000; i++)
if (i != P && d[i] > d[j] && d[i] <= d[j] + 20000){
if (d[i] > d[k]) k = i;
printf("%d %d %d\n", j, i, d[i] - d[j]), m++;
if (j == 1) v[i] = 1;
}
j = k;
}
d[1] = tmp;
for (i = 1; i <= n; i++)
if (d[i] < d[1] && d[i] > d[1] - 10000) break;
printf("%d %d %d\n", i, 1, d[1] - d[i]);
printf("%d %d %d\n", 1, P, d[P] - d[1]);
m += 2;
for (i = 1; i <= n; i++) if (v[i]) printf("%d %d %d\n", P, i, d[i] + 18000 - d[P] + d[1]), m++;
for (i = 1; i <= n; i++)
if (!q[i])
for (j = 1; j <= n; j++)
if (d[i] + 2000 > d[j]){
printf("%d %d %d\n", i, j, 20000);
m++;
if (m == 20000) return 0;
}
return 0;
}
5.算法20。尝试小规模数据发现是强连通分量。。。邪恶的构造又开始了。。。
#include <cstdio>
int main(){
freopen("nm5.in", "r", stdin); freopen("nm5.out", "w", stdout);
scanf("%*d %*d %*d");
for (int i = 1; i <= 5000; i++){
int j;
scanf("%d", &j);
if (i != j)
printf("%d %d 1\n%d %d 1\n", i, j, j, i);
}
return 0;
}
6.算法21。据说是什么东西的Hash。
选一个没有边的3个点的图,发现值是473676905。加了一条边1->2,发现还是这个值。再加上1->3和2->2,发现都是473676905。把1->3变成2->1,发现变成了737394172,再改成一个2与3之间的环又变成了3768644194,再变成一个长为3的环发现变成了3032361454。。。这启发我们可能是算法20+hash。
我们会发现图的点数为8,所以可以用爆搜![]() 关键是——怎么得到Hash值?有一个高大上的方法:就是在终端里输入
关键是——怎么得到Hash值?有一个高大上的方法:就是在终端里输入
./prog nm.out > res
就可以将文件nm.out的运行结果输出进res文件里。在程序里就是这样:
system("./prog nm.out > res");
然后把res里的哈希与正确答案比一下即可。
另外,如果将>改成>>,那么会在文件的末尾追加输出(就是传说中的append)
欺负我那时不会system函数 T_T
再吐槽一句:开始做的时候用wine运行prog.exe\(8!\)遍,结果一万遍的时候就死机了。。。后来找到了linux下的prog。。。千万不要过度迷恋wine。。。
于是程序如下:
#include <cstdio>
#include <cstdlib>
int p[10];
void check(){
int i, s = 0, k;
freopen("nm6.out", "w", stdout);
for (i = 1; i <= 8; i++) if (p[i] != i) s += 2;
printf("8 %d 21\n", s);
for (int i = 1; i <= 8; i++)
if (p[i] != i) printf("%d %d 1\n%d %d 1\n", i, p[i], p[i], i);
fclose(stdout);
system("./prog nm6.out > res");
freopen("res", "r", stdin); scanf("%*d %*d %*d\n%d", &k); fclose(stdin);
if (k == 232615585) exit(0);
}
void dfs(int x){
if (x == 9) check();
else for (p[x] = 1; p[x] <= x; p[x]++) dfs(x + 1);
}
int main(){
dfs(1);
}
跑出来一个这个解。
8 6 21 5 4 1 4 5 1 7 1 1 1 7 1 8 4 1 4 8 1
虽然只有6条边,但是有7分已经很好了!!稍作修改,可以得到这个解。
8 8 21 8 5 1 5 8 1 5 4 1 4 5 1 7 1 1 1 7 1 8 4 1 4 8 1
这个玩意可以拿满分。
7.算法22。一个与强连通性有关的Hash算法。测了3个点的所有情况,如下:
没有边 Hash = 5
1和2在一个强连通分量内 Hash = 2
1和3在一个强连通分量内 Hash = 3
2和3在一个强连通分量内 Hash = 4
全都在一个强连通分量内 Hash = 0
然后发现\(n\)个点全都在一个SCC内哈希是\(0\),而\(n\)个点形成拓扑图哈希是\(n!-1\)。很想知道这是一个怎样的神秘Hash。
受算法20的影响,记\(p_i\)为\(i\)所在SCC内编号最小的点的编号。对于\(n=4\)的情况我又探究了一下,发现\(p=[1,2,3,4]\)时编号23,而\(p=[1,1,3,4]\)时编号是11!这是巧合吗?
下面是一个表。
| p | Hash |
| [1,1,1,1] | 0 |
| [1,1,1,4] | 3 |
| [1,1,3,1] | 8 |
| [1,1,3,3] | 10 |
| [1,1,3,4] | 11 |
| [1,2,1,1] | 12 |
| [1,2,1,2] | 13 |
| [1,2,1,4] | 15 |
| [1,2,2,1] | 16 |
| [1,2,2,2] | 17 |
| [1,2,2,4] | 19 |
| [1,2,3,1] | 20 |
| [1,2,3,2] | 21 |
| [1,2,3,3] | 22 |
| [1,2,3,4] | 23 |
然后我们惊讶地发现。。。
\(Hash = \sum_{i=1}^n{(p_i-1)\prod_{j=i+1}^n{j}}=n!\sum_{i=1}^n{\frac{p_i-1}{i!}}\)
用这个程序输出\(p\)数组的倒序,然后手玩连图。
#include <cstdio>
int main(){
long long int x = 2432898351216220492ll;
long long int i = 20;
while (x){
printf("%lld ", x % i + 1); x /= i; i--;
}
printf("%d ", 1);
return 0;
}
输出
13 13 15 17 8 15 14 13 12 6 5 9 8 7 6 5 4 3 2 1
所以
\(p=[1,2,3,4,5,6,7,8,9,5,6,12,13,14,15,8,17,15,13,13]\)。
连图出来即可。
8.算法30。考场上我是直接使用如下代码企图骗2分走人。。谁想到prog告诉我有10分。。。
据说是二分图匹配?
#include <cstdio>
int main(){
freopen("nm8.out", "w", stdout);
for (int i = 1; i <= 61; i++)
for (int j = 1; j <= 100; j++)
printf("%d %d 1\n", i, j);
return 0;
}
9.算法31。很明显是二分图匹配,输出第\(i\)个数字是左边第\(i\)个点匹配到的右边的点。然后觉得二分图匹配有多个,它会输出哪个呢?大概是字典序最小的那个吧。那么设左第\(i\)个点匹配右第\(f_i\)个点,那么输出\((i,j)\)满足\(j \ge f_i\)。不过一想发现只有5050条边。嗯。。还有被以前的点匹配过的也不行。于是又把满足\(j<i\)的\((i,f_j)\)输了一遍。发现有10000条边,还有重边!去重之后就是7653条了,正好。
#include <cstdio>
int f[1000];
int k[1020][1020];
int i, n, m, j;
int main(){
freopen("nm9.in", "r", stdin); freopen("nm9.out", "w", stdout);
scanf("%d %*d %d", &n, &m);
for (i = 1; i <= n; i++) scanf("%d", &f[i]);
for (i = 1; i <= n; i++){
for (j = 1; j < i; j++) printf("%d %d 1\n", i, f[j]), k[i][f[j]] = 1;
for (j = f[i]; j <= 100; j++) if (!k[i][j]) printf("%d %d 1\n", i, j);
}
return 0;
}
10.算法13。(不会做。)又名【写挂了的SPFA算法】。可以用来防AK。
后记
其实这题剧透了没什么味。要在考场上能玩出来才厉害。
2015
【kcut】
orz 鼎爷
orz africamonkey
orz hack狂魔qmqmqm
积极投身于FST事业
。。在bzoj上垫底,uoj上被hack了然后无法翻身。。同一个复杂度,我的运行时间是别人的十几倍?或者我复杂度错了?欢迎打脸
四个程序。
0.判断数据类型 不用说了
1.暴力 不用说了
2.$k$短路
考虑一张单源dag,边权都是非负整数,源点$s$到一个点的所有路径长度一样。记$s$到$x$的路径的长度为$d(x)$,我们需要在遍历尽量少的节点的情况下求出前$k$小的$d(x)$。
最小的显然是$d(s)$。那么我们把$s$入堆。
每次选一个元素$x$出堆,并把$x$的后继节点(如果没有进入过堆的话)加入堆中。堆的权值是节点的$d$值。
如果dag的每个点的出度是常数,那么这样的复杂度是$O(k\log k)$的。
我们可以把这个题转化为dag模型。首先对图进行重标号,使得$s=n-1,t=n$。然后如果$w(s\to i)>w(i\to t)$,那么交换两条边的权值,不会影响答案。那么我们令$A_i=(w(s\to i),w(i\to t),w(s\to i)+w(i\to t))$。每个点用一个长度为$n-2$的三进制串表示,第$i$位为$0$则表示割掉$s\to i$,为$1$则表示割掉$i\to t$,为$2$则表示都割掉。一个点$s$的$d$值就是$\sum_{i=1}^{n-2}A_{i,s_i}$。
现在连边需要满足三个条件:
- 每个点的度数都是常数;
- 给出一个点的$d$,可以$O(1)$计算后继点的$d$值;
- 所有边的权值都是非负的。
我们考虑这样连边:对于一个三进制串$s$我们可以求出它最后一个非0数$s_i$,然后有$3$种连边:
- 如果$s_i<2$,$s_i\to s_i+1$;
- 如果$i<n-2$,$s_{i+1}\to 1$;
- 如果$i<n-2$且$s_i=1$,$s_{i+1}\to 1,s_i\to 0$。
其中前两种边的权值显然是非负的,第三种边的权值是$(A_{i+1,1}-A_{i+1,0})-(A_{i,1}-A_{i,0})$,那么把边按照$A_{i,1}-A_{i,0}$排序之后,第三种边的权值是非负的。
然后在这个图上找$d$最小的$k$个点。就行了。
3.$k$小割
设最小割为$C_1$。首先考虑次小割$C_2$。。如果$C_1$中有一条边不在$C_2$中,那么次小割就是强制这条边容量为$+\infty$之后的最小割。否则次小割就是最小的不在$C_1$中的边并上$C_1$。这样求次小割的复杂度是$O(m\times \text{networkflow}(n,m))$的。
不妨优化这个算法,把复杂度优化到$O(n\times \text{networkflow}(n,m))$。考虑一条割边$a\to b$,把它的容量设为$+\infty$之后最大流会增加多少?就是$s\to a$的可增广量与$b\to t$的可增广量的较小值。这样我们只需要求出每一个点到$s$或$t$(具体看它在哪个割集中)的可增广量即可。
考虑另一个问题,假设所有割集的全集为$CS$(即$\forall s\in CS$,$s$是原图的一个割)。$w(s)$表示一个割集$s$的边权和。我们可以这样求第$k$小割:
首先从$CS$中求出最小割$C_1$和次小割$C_2$;
然后令$CS=CS_1\cup CS_2$,其中$C_1\in CS_1,C_2\in CS_2$。显然$C_1,C_2$分别是两个集合的最小割。我们可以求出两个集合的次小割,假设其中较小者为$C_3$,且$C_3\in CS_1$。
然后令$CS_1=CS_{11}\cup CS_{12}$,其中$C_1\in CS_{11},C_3\in CS_{12}$。显然$C_1,C_3$分别是两个集合的最小割。我们可以求出两个集合的次小割$C_4,C_5$,和$C_2$一起比大小,假设其中最小者为$C_4$,且$C_4\in CS_{11}$。
$\dots\dots$
然后我们就求出了前$k$小的割集大小。
如果我们把每一个集合$s$都规定成这个样子,用两个边集$(I_s,O_s)$来表示:$I_s$中的边要求必须被割,$O_s$中的边要求不能被割。那么$s$中的最小割和次小割都是很好求的。只要最小割与次小割的对称差中有一条边$e$,那么我们就可以把集合$(I,O)$分割为$(I\cup\{e\},O)$和$(I,O\cup\{e\})$这两个集合。
所以就这样啦~
【pdt】
vfk的博客说得很清楚了。
做一些入门向的补充。。如有错误恳请提出。。窝的线代很渣的
-
蟑螂与变形虫是好朋友。 - 题目意思。。就是给了一个“混淆版算法”(一个函数),要求一个函数跟它相差$<1\%$。你要求的函数一定能写成只与$m$个($x_{a_1}\oplus x_{a_2}\oplus \dots\oplus x_{a_i}$)相关的函数。我们可以把题目看成两部分:求$f_A$($f_A$表示系数)很大的一些$A$;根据这些$A$推算$h$函数。
- $f_A=\frac{1}{2^n}\sum_{\mathbf{x}}f(\mathbf{x})(-1)^{\mathbf{v\cdot x}}$,其中$v_i=[i\in A]$的证明。。因为消去一个元素$x_1$就是$f'(x_{2\dots n})=\frac{1}{2}(f(1,x_{2\dots n})+f(-1,x_{2\dots n}))$而强制保留一个元素$x_1$就是$f'(x_{2\dots n})=\frac{1}{2}(f(1,x_{2\dots n})-f(-1,x_{2\dots n}))$,所以上面的式子相当于一步步确定每个元素是否保留,在$A$中的保留否则去掉。
- $\frac{1}{2}(f(x)-f(x+\mathbf{v}))$保留了$f$的所有与$\mathbf{v}$点积为$1$的分量。$\frac{1}{2}(f(x)+f(x+\mathbf{v}))$保留了$f$的所有与$\mathbf{v}$点积为$0$的分量。这是因为,考虑一个分量$\mathbf{Q}$,假设$\mathbf{Q}\cdot \mathbf{v}=0$,那么在第一个函数中$$f_{\mathbf{Q}}=\frac{1}{2^{n+1}}\sum_{\mathbf{x}}(f(\mathbf{x})(-1)^{\mathbf{Q\cdot x}}-f(\mathbf{x})(-1)^{\mathbf{Q\cdot (x+v)}})$$而$\mathbf{Q\cdot (x+v)=Q\cdot x+Q\cdot v}$。故$f_{\mathbf{Q}}=0$。而如果$\mathbf{Q}\cdot \mathbf{v}=1$那么$f_{\mathbf{Q}}$就是原来函数中那个系数。
- 接下来的算法中我们需要随机$s$个线性无关的向量$\mathbf{v}_1,\dots,\mathbf{v}_s$。
- 令$F(\mathbf{x})$表示一个大小为$s$的向量,其第$i$维的值是$\mathbf{x}\cdot \mathbf{v}_i$的值。令$c_1,c_2,\dots,c_{2^m}$表示系数很大的那些分量。那么【帅气的算法】中的$U$指的就是$F(c_1),F(c_2),\dots,F(c_{2^m})$。
- 我们可以检查是否存在$F(c_1)=k$。就是用第3条中所说的方法。即考虑函数$$f'(x)=\frac{1}{2^s}\sum_{s_0\subset \mathbf{v}}{(-1)^{\sum_{\mathbf{u}\in s_0}[\text{强制要求$u\cdot c_1=1$}]}f(x+\sum_{\mathbf{u}\in s_0}\mathbf{u})}$$其保留了所有$F=k$的分量。
- 我们可以取$s=6$,遍历64个元素看哪些是某个$F(c_1)$。如果有$2^m$个,且其rank为$m$,我们就找到了【帅气的算法】中的$U$。
- 给出了$F(c)$我们当然希望求$c$。$F(c)$提供了什么信息?提供了“这个分量与$s_i$的点积是$F(c)_i$”,我们只要通过第3条使得$F$只含这一个分量,然后对每个$x_i$求出它是否在这个分量中即可。
- 我们还需要算出$h$值。。比如说要求$h$的某一项$h(d_1d_2\dots d_m)$,假设可以确定$x$的取值(随机乱取TAT)使得$c$数组恰好就是$c_i=d_i$,然后代入$f$求值就是$h$啦。
- 我至今不知道这题怎么构造数据和怎么写checker(checker可能随机一下就可以了吧)。但是这题是可以拍的。。。只要你把小强给的“混淆版算法”改成手写黑盒子(你是知道这个黑盒子的答案和噪音的)即可。
- 考虑样例1(见uoj),混淆版函数$f=11101110=x_0\text{ nand }x_1$,可以写成$-0.5x_0-0.5x_1+0.5x_0x_1-0.5$(注意$x_i\in\{1,-1\}$)。拿向量$\mathbf{v}=\{1,0,0\}$来说,$f(x)-f(x+v)=-x_1-1$,只保留下了分量$x_1$与分量$1$。
- 我开始取$s=5$的时候在uoj上挂了10分,改成$s=6$发现挂了30分。wyh2000机智地跟我说“把$s$改成4”(此时他并不会做这个题)然后我死马当做活马医 A了。
- 这个题我看了一整天题解,调了一整天。所以一共用了两天时间做。T_T
Q:做小强题目有什么好处 A:打发时间
【program】
傻逼360云盘失效了。。点我
【参考资料】
http://africamonkey.blog.uoj.ac/blog/108
http://vfleaking.blog.uoj.ac/blog/104
http://fanhq666.blog.163.com/blog/static/8194342620121185107104/
钱桥《平面图的处理方法》
胡伯涛《最小割模型在信息学竞赛中的应用》
陈立杰《wc2013解题报告》