请轻喷。。

代码http://pan.baidu.com/s/1sjwqxzR   提取密码p6vf(好像并不需要密码)

(15年的题目代码去uoj上看吧)

(反正不会有什么人闲着蛋疼去看我代码)

引用的题解都是搜索引擎中输入题目名称得到的第一条(或者前面的)搜索结果。

做完15年的题就停更。

【transform】

字典序最小的二分图完备匹配。

一个并不清楚正确性的算法：从\(n\)到\(1\)枚举左边点，对每个点从\(1\)到\(n\)枚举右边点。

【poet】

二分栈。时间复杂度\(O(tn\log n)\)。

设\(len_i\)表示句子\(i\)的长度，\(s_i\)表示\(\sum_{k=1}^i{(len_k+1)}\)。那么dp转移方程可以手写。

\(f_i=\max_{0\le j<i}{f_j+(s_i-s_j-1-L)^P}\)

为什么有决策单调性呢？(不知道

具体实现的时候可以拆成两个问题写：

1.求最优排版

2.输入句子、给定排版来输出

【treapmod】

觉得这题也好神啊。= =||

orz http://blog.csdn.net/pouy94/article/details/5917209

状态是将节点按照数据值排序并将权值离散化之后\(f_{l,r,w}\)表示区间\([l..r]\)建出一棵树且根节点权值不小于\(w\)的最优解。

网友说因为\(w\)有后效性所以要加入状态中。

唉。知道状态了之后就不难了。。但是很多dp题的状态都不容易搞出。。

【pvz】

显然是最大权闭合图吧。。。

但是这个题的图有环！！显然环上的点是不能选的(这与普通的最大权闭合图有一点区别)，如果需要选环上的点才能选某个点\(u\)，那么点\(u\)也不能选。

所以找环是关键。

开始的想法是：如果\(i\)和\(j\)能互达，那么\(i\)和\(j\)都不能选。其他的可以选。结果WA了两个点(数据其实比较水，只错两个点)。后来一想。有可能出现上述说的点\(u\)的情况。例如如下样例的答案是1。

2 2
1 1 1 1
1 0
1 0
1 1 0 0

那么到底该怎么做呢？注意到如果一个点能走回自己，那么就不可以选这个点。如果选了某个点\(u\)就必须选一个“不可以选”的点\(v\)，那么\(u\)也是不可以选的。

这样就能A了。

【ball】

神题。

考虑开两盘游戏。假设都玩到了同一个输出序列\(i\)。那么游戏1有\(a_i\)种方法玩到这个序列，游戏2也有\(a_i\)种方法。这样就有\(a_i^2\)种方法玩到这个输出序列。

设游戏1玩到上管道取了\(i\)个，下管道取了\(j\)个；游戏2上管道取了\(k\)个，下管道取了\(l\)个；且它们玩出的序列是相同的。用\(f_{i,j,k,l}\)表示可能的玩法的数目。那么\(f_{n,m,n,m}\)就是所求的解。

转移方程随手写。

注意到\(i+j=k+l\)。可以省掉一维。

这样可以拿90分。

当\(f_{i,j,k}\)为0的时候不进行转移。这个优化加了之后就可以爆虐100分了。

【path】

使用自适应simpson等算法可以拿97分。

为了防止写挂，可以拿一个暴力对拍。暴力就用随机撒点写好了。暴力的精度并不好，大概是1或者0.1吧。

具体地分析一下。simpson需要的量是直线\(x=x_0\)被图形覆盖的长度。而图形可以拆成一堆半径一定的圆和一堆宽一定的长方形。设圆的半径为\(r\)。

对于圆心在\((x,y)\)的圆，设\(d=|x-x_0|\)。如果\(d\ge r\)，那么可以看作没有覆盖\(x=x_0\)这条直线；否则令\(D=\sqrt{r^2-d^2}\)，覆盖区间是\([y-D,y+D]\)。

对 于矩形。由于情况很多，不做讨论。换一种思路，就是给四条线段，求\(x=x_0\)与它们各自的交点。但是\(x=x_0\)最多与两条线段有交点。对 于一条连接\((x_1,y_1)\)与\((x_2,y_2)\)的线段，我们默认其斜率存在，为\(k=\frac{y_2-y_1}{x_2- x_1}\)。再求出其截距。于是直线\(x=x_0\)与其交于一点\((x_0,kx_0+b)\)。当\(x_0\)在\(x_1,x_2\)形成 的区间中，即\((x_0-x_1)(x_0-x_2)<0\)时有交点。取两个交点作为覆盖的区间。

另外，对于竖直的矩形需要特判。

把区间都收集好之后就开始做线段覆盖了。求出这些区间覆盖的总长度即可。

关于暴力的一点：如何判断点在矩形中：由于矩形就是到中轴线的距离不超过\(\frac{r}{2}\)，且投影在中轴线段上的点的集合，所以直接判即可。

upd

写完了。又是什么少了个\(r\)没乘之类的低级错误。幸好对拍了，否则就是只有10分了。

拿了97分。暴力也拿了38分，精度还好。

其中第10个点跑了16min+，第9个点跑了3min+，其他点都是秒出。

暴力只跑了8个点。

【energy】

求的就是

\(\sum_{i=1}^n{\sum_{j=1}^m{2\gcd(i,j)-1}}\)

\(=2\sum_{i=1}^n{\sum_{j=1}^m{\gcd(i,j)}}-mn\)

\(=2\sum_{k}{k\sum_{i=1}^{\lfloor \frac{n}{k}\rfloor}{\sum_{j=1}^{\lfloor \frac{m}{k}\rfloor}{[\gcd(i,j)=1]}}}-nm\)

\(=2\sum_{k}{k\sum_{t}{\mu(t)\lfloor\frac{n}{kt}\rfloor\lfloor\frac{m}{kt}\rfloor}}-nm\)

时间复杂度\(O(n\log n)\)已经够了。

不过可以继续优化。

\(=2\sum_{x}{\lfloor\frac{n}{x}\rfloor\lfloor\frac{m}{x}\rfloor\sum_{k|x}k\mu(\frac{x}{k})}-nm\)

\(=2\sum_{x}{\lfloor\frac{n}{x}\rfloor\lfloor\frac{m}{x}\rfloor d(x)}-nm\)

所以可以\(O(n)\)做。

【piano】

首先转前缀和。令\(s_i=\sum_{j=1}^i{A_i}\)。

然后发现可以\(O(1)\)算出和弦的美妙度。

考虑\(k=1\)的情况。那么扫描所有的\(i\)，即令和弦为\([i+1..j]\)，每个\(i\)都有一个\(j\)的区间，也就是\([i+L,i+R]\)。通过动态维护这个区间中的最大值可以求出答案。

假 设我们给每一个点\(i\)开一个堆\(H_i\)存储\([i+L,i+R]\)的\(s\)值。再令点\(i\)的权值\(w_i\)为\(H_i \)顶部的\(s\)值减去\(s_i\)的值。也就是如果左端点选\(i+1\)的话能达到的最大值。把\(w_i\)用一个堆维护。每次取出 \(w_i\)的最大值当作答案，然后在这个数据结构中删除这个最大值，更新\(w_i\)。

一个问题：要开那么多个堆吗？不用。我们有可持久化线段树(=可持久化堆)。(小心空间= =)

主席树空间好大的说= =

【altitude】

首先。一个城市的海拔不是0就是1。

然后就是最小割=>最短路了。

有一个问题需要弄清楚。例如，原图中一条从左到右的有向边，在新图中是从上到下还是从下到上呢？我们这么想。

假设在最大流中这条边左边是0，右边是1。再随便添加几个点，如图。

在 最小割转最短路的时候有一步操作是在\(s\)和\(t\)之间连一条弧线，把无穷域劈成两半，一半作为对偶图中的\(s\)，一半作为对偶图中的\(t \)。假设如图的一半是\(s\)，一半是\(t\)。画出连接割的路径，这条路径要从\(s\)走到\(t\)。会发现它从上面穿过了这条边。故连的有 向边是从上到下的。

1A好开心～

【plane】

想出来了～

以第二类限制为有向边建图。这个图一定是DAG。

然后考虑 顺着拓扑序确定每一个点的起飞序号，发现这样是做不了的。为什么呢，因为这样做有后效性：你确定了前面的点，可能与后面的点冲突了，从而使得后面的点没有 可能的起飞序号。那么怎样才能消灭后效性呢？很简单：从后往前贪心即可。也就是说，每一次取拓扑序后面的一个点，并让它的时间尽量大。这样第一问就完了～

第二问的方法也异常简单。对于每个点，先贪心所有这个点不影响的点，然后得到的答案就是最小的。

再就是我们在此题中需要维护一个集合(可以用的起飞序号集合)。支持快速地：

• 删除
• 求不大于\(x\)的最大元素

这个用并查集随便搞搞就行了。复杂度\(O(n(m+n\log n))\)，但是实际上可以通过所有点。

【trip】

插头dp。太难了~~~

【nemo】

point 1

用于熟悉题目意思。

就是先跑到一个地方去吃一条虾，然后过去追另一条虾。

然后答案就是形如

2
20
t1 0 10+t1 1
t2 10+t2 0 2

对着checker调\(t_1,t_2\)即可。

调出一个这个东西。

2
20
1.2 0 11.2 1
3 13 0 2

point 2

\(n=8\)摆在这儿了。搜吧。

其实这个点我调了一个多小时T_T。。但是这个点做出来了后面的点才可能做出来。。

还有一个坑爹的地方是最优解不是8个全吃掉。。

主要卡在哪儿呢，就是求nemo吃到某个小虾的最短时间。开始列方程发现细节太多(很多根是负数)，然后使用暴枚发现精度与时间无法调整，最后改成了三分套二分。

我们知道要求的是一个奇奇怪怪的二次函数在\([0,t]\)内的最小零点。那么可以三分找到极小值，那么在0与极小值之间二分找零点。

point 3

发现重量都是互不相同的2的幂。只有唯一的吃的顺序。

而且算出来用时是570点几，时间限制是571，正好。

point 4

有“排序强迫症”的人应该会赚翻。

按照横坐标排序之后发现中间那部分简直是福利啊。。。

124 -14 0 0 0
167 -13 0 0 0
12582912 -12 0 0 0
6291456 -11 0 0 0
3145728 -10 0 0 0
49152 -9 0 0 0
24576 -8 0 0 0
12288 -7 0 0 0
6144 -6 0 0 0
3072 -5 0 0 0
384 -4 0 0 0
192 -3 0 0 0
96 -2 0 0 0
48 -1 0 0 0
6 1 0 0 0
12 2 0 0 0
24 3 0 0 0
768 4 0 0 0
1536 5 0 0 0
98304 6 0 0 0
196608 7 0 0 0
393216 8 0 0 0
786432 9 0 0 0
1572864 10 0 0 0
100 11 0 0 0
158 12 0 0 0

所以吃完这些东西然后选一个方向一路吃过去即可。

point 5&6

发现nemo只能在\(x\)轴上动。然后每个小虾\(i\)等于一个点，它定时出现在\(x\)轴的某个位置\(pos_i\)。

按照时间顺序排序，然后有dp方程

\(f_i=\max{f_j}+w_i\)

其中要求nemo吃完\(j\)之后立马赶到\(i\)将会出现的位置，不会太晚。即

\(|pos_i-pos_j|\le(t_i-t_j)speed_{nemo}\)

还有记得一定是小于等于而不是小于。否则第6个点会挂。

point 7&8

发现是数字三角形，于是dp即可。

point9&10

随机？随不出特别好的解～

贪心？yes！

point9，每次找最快吃到的小虾，可以在时限内把小虾吃光。

point10，按照同样的方法可以吃掉4500多个小虾。

于是nemo这题前9个点可以A，第10个点只有6分。第10个点可能需要其他的贪心技巧。

【rabbit】

不会做

【car】

矩形的顶点($x$相同的四个点我们只考虑中间两个)和$S,T$作为关键点，两点直线不经过矩形的边那么可以连边。然后求最短路。SSSP用spfa应该不会有错。关键是判连边。(至少暴力的$O(n^3)$有了吧。)

考虑一个点能够到达哪些点。$S,T$能够到达的点我们直接用暴力判；矩形的端点能够到达的点我们只考虑其右部的。维护一个极角区间，每加入一个矩形我们更新这个极角区间。就可以了。

【type】

AC自动机水题

提示：从点$x$沿着fail链往上跳可以遍历$x$的所有在trie中的后缀

【road】

太神啦不会做>_>

【show】

很神的dp(真的很神)。膜题解blog.csdn.net/whjpji/article/details/7547159

首先离散化。

我们令$num_{i,j}$表示包含于区间$[i,j]$的区间个数，$pre_{i,j}$表示从$num_{0,i}$中选$j$个区间到嘉年华2，那么最多选多少个区间到嘉年华1。$suf_{i,j}$表示从$num_{i,+\infty}$中选$j$个区间到嘉年华2，那么最多选多少个区间到嘉年华1。

怎么转移呢。。。

$$pre_{i,j}=\max(pre_{i,j+1},\max_k(pre_{k,j}+num(k,i),pre_{k,j-num(k,i)}))$$

$$suf_{i,j}=\max(suf_{i,j+1},\max_k(suf_{k,j}+num(i,k),suf_{k,j-num(i,k)}))$$

第一问的答案就是$\max(\min(j,pre_{+\infty,j}))$。

第二问。。令$g(i,j)$表示必须选取$num_{i,j}$中所有区间，且这些区间都在嘉年华1时的答案。那么

$$g(i,j)=\max_{0\le x+y\le n}(\min(pre_{i,x}+suf_{j,y}+num_{i,j},x+y))$$

对于$i$的答案就是$\max_{l\le L[i]\le R[i]\le r}g(l,r)$。

据说有决策单调性。固定$i,j$，$x$加的时候$y$减。就这样了。

【game】

首先介绍二分图模型：一个二分图$G$，上面有一个石子。石子总是在一个点上。先手后手轮流操作，每个人可以把石子放到一个以前没有被石子访问过、且与当前石子所在的点相邻的点上。不能操作者输。

一方面，如果存在一个最大匹配$M$使得$M$不包含石子的初始位置，那么后手有必胜策略。首先，先手的第一步一定是移动到一个已匹配的位置(不然$M$怎么会是最大匹配呢=w=)，然后后手沿着匹配边移动即可。那么会不会什么时候先手走完之后到达了一个未盖点呢?不可能，因为否则的话就找到了一条增广路，$M$就不是最大匹配了=w=。

另一方面，如果石子无论如何一定在一个最大匹配中(一种特殊情况是，该图有完备匹配)，那么先手有必胜策略。先手只要找一个最大匹配$M$，然后每次沿着匹配边移动。后手不可能把石子移动到未盖点，否则就找到了一个(增广路减一条非匹配边这种东西)，沿着它可以构造出一个与$M$同样大小的匹配，它不包含石子的初始位置。

所以这个题就变成了：首先删掉石子的初始点求一遍最大匹配，然后加上石子的初始点。如果顺着石子的初始点不能找到增广路，那么后手胜，否则先手胜。

我们一步一步地分析原题。

首先，我们把移动操作$M(x,y)$看作是空格移动到了$(x,y)$这个位置。于是在游戏的过程中，空格形成了一条路径。

其次，这条路径是不会形成环的。否则假设是兔兔执行了$M_1(x,y)$之后空格第一次到达$(x,y)$这个点，那么一定是兔兔(而不是蛋蛋)执行了另一次$M_2(x,y)$之后第二次到达这个点(环长是偶数)。考虑$M_1(x,y)$之后蛋蛋将一个黑棋子$B$移入空格。那么兔兔的$M_2(x,y)$相当于将$B$从$(x,y)$中移出。。。但是兔兔是不允许移动黑棋子$B$的。所以这条路径不会形成环。

接下来会发现把棋盘红蓝相间地染色之后，如果空格染蓝色，那么兔兔每次移动相当于将空格(看成一个石子)从蓝色格子(看成二分图的$X$部)移动到红色格子(看成二分图的$Y$部)；蛋蛋每次移动相当于将石子从$Y$部移动到$X$部。同时，不是所有移动都是可行的：如果在原来的棋盘中，$i$与$j$相邻且$j$是一个白色棋子，那么兔兔可以把石子从$i$移动到$j$；如果在原来的棋盘中，$i$与$j$相邻且$j$是一个黑色棋子，那么蛋蛋可以把石子从$i$移动到$j$。

我们这样构建二分图：取出$X$部的所有黑色格子与$Y$部的所有白色格子，以及初始局面的空格(空格属于$X$部)，每相邻的两个格子之间连一条边。问题变成了上面二分图上的博弈。我们要求的问题就是，每次判断一个局面是不是先手必胜，然后走两步棋(当然也删掉了两个已访问格子)。

暴力判断最大匹配好像可以过哦。复杂度$O(kn^2m^2)$。

【random】

\(x_{n+1}=(ax_n+c) \mod m\)

求$x_n \mod g$

很简单的矩阵乘法。

$\left[
\begin{array}{ccc}
x_i & 1
\end{array}
\right]
\times
\left[
\begin{array}{ccc}
a & 0 \\
c & 1 \\
\end{array}
\right]
=
\left[
\begin{array}{ccc}
x_{i+1} & 1
\end{array}
\right] $

一定要注意两个longlong相乘。。。。

【bicycling】

拉格朗日乘数大法。

很久以前做完的，题解坑(bu)在(zhun)这(bei)儿(xie)吧(le)

【chess】

在某个神犇(sy还是jzp，反正是百度空间)的博客里看到的。

如图，假设黄色点是棋盘守护者，那么黄色点维护自己的值，红色点维护自己的值减去(自己旁边离黄色点最近的红色点的值)，橙色点维护自己的值减去两边的值加上对角的值。。。就是差分。

例如$A$维护的值是$A+D-B-C$，$E$维护$E+H-G-F$，$W$维护的值是$W+Z-X-Y$，$P$维护的值是$P-Q$，$X$维护$X-Z$，$Z$就维护$Z$自己。

查询的话就直接查询矩阵gcd。修改的话。。讨论吧。

这题简直恶心啊= =。简直恶心啊= =。简直恶心啊= =。(重要的话说三遍

写了个四分树，听说复杂度不对，不管了。随手构了一个$n=m=707$的数据卡到13s+。。。拿来一测发现居然过了。。。

【park】

很久以前做完的，题解坑(bu)在(zhun)这(bei)儿(xie)吧(le)

【delicacy】

@scoi2007 修车

题意抽象之后就是：左边有$p$个点，编号$1\sim p$，每个点有一个$1\sim n$的属性$a_i$；右边有$m$个点，编号$1\sim m$。现在左边的每个点$i$要求连到右边一个点$f(i)$。对于右边的一个点$j$，设$x_1,x_2,\dots,x_l$($x$是有序数组)连向$j$，那么代价为$\sum_{i\le l}i\times t_{a_{x_i},j}$，最小化总代价。

这么建图：对于右边一个点$j$拆成无穷个点，第$i$个点连向所有左边点$x$的代价为$i\times t_{a_x,j}$。

考虑优化构图。首先左边的点数顶多$n$个就够了；其次可以先放$m$个点上去，一个点被匹配了那么加入它后面的点。

【tritown】

【meow】

给出\(n\)个\(d\)维向量\(x_{ij}\)，问是否存在两个向量内积为\(k\)的倍数。

时限貌似是5秒。

数据分两种：

\(k=2,n \le 20000, d \le 100\)与\(k=3,n \le 100000, d \le 30\)。其实还有一个数据\(n=10000, d=100, k=3\)。

【开胃菜】给出三个\(n \times n\)的矩阵\(A,B,C\)，\(O(n^2)\)判断\(A \times B = C\)是否成立。很经典的一个模型。随一个\(1 \times n\)的向量\(v\)，然后判断\(v \times A \times B=v \times C\)是否成立即可。多随几次就行了。

【\(k=2\)】定义矩阵\(M_1\)的第\(i\)行第\(j\)列表示第 \(i\)个向量与第\(j\)个向量的内积\(\sum_{k=1}^d{x_{ik}x_{jk}}\)。定义矩阵\(M_2\)为\(n \times n\)的矩阵，其对角线元素就是\(M_{2ii}=\sum_{k=1}^d{x_{ik}^2}\)，其他元素均为\(1\)。为了判断 \(M_1=M_2\)是否成立，我们随机一个向量\(v\)，并计算\(v \times M_1\)与\(v \times M_2\)。

注 意到\(M_{1ij}=\sum_{k=1}^d{x_{ik}x_{jk}}\)，所以\(M_1\)就是\(x\)与\(x^T\)相乘，于是我们 计算\(v \times x \times x^T\)。复杂度是\(O(nd)\)的。而\(v \times M_2\)呢，有

\((v \times M_2)_{i}=\sum_{j=1}^n{v_jM_{2ji}}=(\sum_{j=1}^n{v_j})-v_i+v_iM_{2ii}\)。

算这个玩意也是\(O(nd)\)的。

但 是，如果\((v \times M_1)_i \ne (v \times M_2)_i\)，我们如何找到两个向量\(x_p,x_q\)使得他们的内积为\(0\)呢？因为\((v \times M)_i\)只受到\(M\)的列\(i\)的影响，所以\(p\)和\(q\)中有一个是\(i\)。然后枚举另一个即可。这也是\(O(nd)\) 的。

于是我们圆满地解决了\(k=2\)的问题。

【\(k=3\)】因为模\(3\)意义下\(1^2=2^2\)，所以我们不妨对\(M_1\)中的每个元素平方，仍称作\(M_1\)。

首 先解决平方的问题。因为\((\sum_{k=1}^d{x_{ik}x_{jk}})^2= \sum_{k=1}^d{\sum_{l=1}^d{x_{ik}x_{il}x_{jk}x_{jl}}}\)，故可以写出一个\(n \times d^2\)的矩阵\(X\)。如果\(d\)进制下小于\(d^2\)的某个数\(t\)最低位为\(k\)，最高位为\(l\)，且\(1 \le i \le n\)，那么令\(X_{it}=x_{ik}x_{il}\)。我们惊奇地发现\(M_1=X \times X^T\)！

然后判断\(M_1=M_2\)是否成立即可。复杂度是\(O(nd^2)\)。注意由矩阵\(X\)的对称性，这个\(d^2\)的常数因子可以化为\(0.5\)。

还有在bzoj上可以过在uoj上死活过不去是什么回事

【count】

【train】

这题最蛋疼的地方是读入。

每个点都是差不多的模型：一开始v 2 + c 什么，然后每一大块是一些可选可不选的v $i$ + c $x$，到最后结算一下所有$3\sim m$变量的绝对值之和再把变量清零。每一块可以选择跳过，如果不跳过那么需要付一定费用(v 2)。有的时候有“只有进入块$i$才能进入块$j$”的限制，限制关系形成一棵树。

point 1是两个点的链。去了一个就不能去另一个。

point 2是一个点。

point 3是没有v 2限制的链。

point 4是链上的背包。

point 5是树上的背包。

point 6是加大范围的树上背包。

point 7是有v 2限制的链。

point 8是数据范围加大的point 7。

point 9是树。

point 10是数据范围加大的point 9。

对每一块使用爆搜求出这一块的决策及对v 1的贡献，然后树形dp，$f[i][j]$表示用$j$的代价玩子树$i$最多玩出多少。

好像树的dp写错了，所以这题我只有95分。T_T

【matrix】

已知

\(F[1][1]=1,F[i][j]=a\times F[i][j-1]+b(j\ne 1),F[i][1]=c \times F[i-1][m]+d(i \ne 1)\)

求\(F[n][m] \mod 10^9+7\)。

数据范围：\(n,m \le 10^{1000000},a,b,c,d \le 10^9\)。

首先建立递推关系。

\(F[i][2]=aF[i][1]+b\)

\(F[i][3]=aF[i][2]+b=a^2F[i][1]+(a+1)b\)

\(F[i][4]=aF[i][3]+b=a^3F[i][1]+(a^2+a+1)b\)

依此类推，发现

\(F[i][m]=a^{m-1}F[i][1]+(a^{m-2}+a^{m-3}+...+a+1)b=a^{m-1}F[i][1]+\frac{a^{m-1}-1}{a-1}b\)

所以

\(F[i+1][1]=cF[i][m]+d=ca^{m-1}F[i][1]+c\frac{a^{m-1}-1}{a-1}b+d\)

另外地，\(a=1\)时要特判。

令

\(p=ca^{m-1},q=c\frac{a^{m-1}-1}{a-1}b+d\)

即

\(F[2][1]=pF[1][1]+q\)

\(F[i][1]=p^{i-1}F[1][1]+(1+p+p^2+...+p^{i-2})q=p^{i-1}F[1][1]+\frac{p^{i-1}-1}{p-1}q\)

算出\(F[n+1][1]\)。然后

\(F[n+1][1]=cF[n][m]+d \Rightarrow F[n][m]=\frac{F[n+1][1]-d}{c}\)

然后除法很好办(因为\(10^9+7\)是质数，有逆元；\(p=1\)特判)。

算法步骤：算\(p,q\)，然后算答案。

用到一个叫做十进制快速幂的东西。即我们要算\(q^a \mod p\)，已知\(a=\sum_{i=0}^n{a_i}\)。有

\(A_n=q^{a_n}\)可以直接算。

\(A_{n-1}=q^{10a_n+a_{n-1}}=(q^{a_n})^{10} \times q^{a_{n-1}}=(A_n)^{10} \times q^{a_{n-1}}\)

\(A_{n-2}=(A_{n-1})^{10}\times q^{a_{n-2}}\)

。。。这么推过来就行了。

其实蛮好写的。

【penman】

这种题出到noi里去让不让人活

毁掉了我对noi题目小清新的认识啊啊啊(noi什么时候小清新过了)

一根竖着的扫描线$t$从右往左扫，记录一下扫描线的状态$(type,a,b)$。

type是nl,nm,nr,ol,om,or,il,im,ir中的一个，$(a,b)$是参数。

nl表示N中最左边的矩形，nm表示中间的矩形，nr表示N中最右边的矩形。

ol表示O的最左列，om表示O的中间列，or表示O的最右列。

il表示I的第二个矩形左边，im表示I的第二个矩形，ir表示I的第二个矩形右边。

(下图N的错了。。n1和n2分别是nl和no。。nr就是n2右边那个竖的矩形。

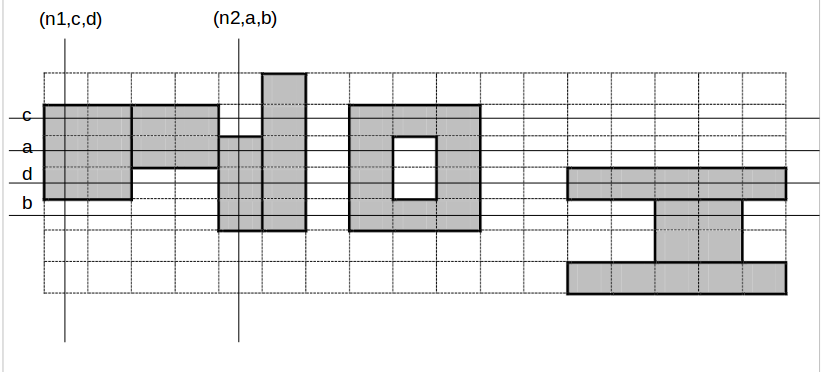
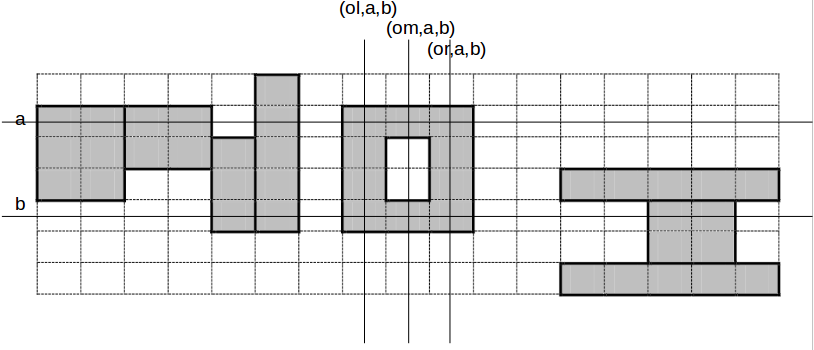
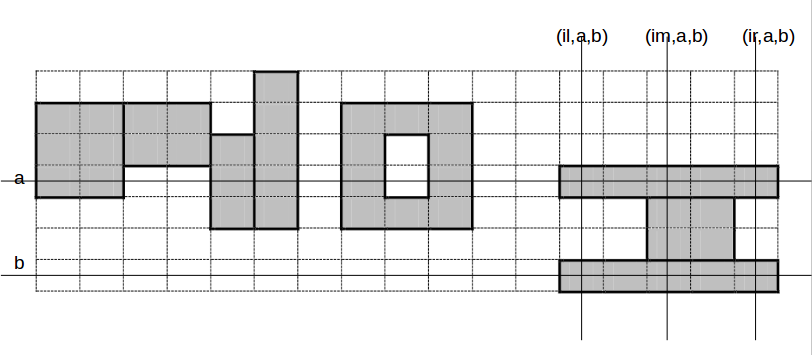
暴力转移是$O(n^4m)$，前缀和优化可以做到$O(n^2m)$。

多一个log好像就会被卡。

其实还好啦～

【foodshop】

考虑暴力。枚举删掉一条非树边，求出剩下的树的直径长度除以$2$，取min即可。

令$len$为环长，环上的点分别是$r_1,r_2,\dots,r_{len}$，环下的树直径分别是$d_1,d_2,\dots,d_l$，第$i$棵树中到点$r_i$最远的点到$r_i$的距离为$l_i$。$dist(i,j)$表示删除$(r_1,r_n)$这条边之后，点$i$与点$j$之间的距离。

令$PT_i$表示环的前$i$棵树链在一起形成的树(类似于前缀和)，$pd_i$表示$PT_i$的直径，$pl_i$表示$PT_i$中离$r_1$最远的点到$r_1$的距离，$ql_i$表示$PT_i$中离$r_i$最远的点到$r_i$的距离。可以dp：

$$pd_i=\max(pd_{i-1},d_i,ql_{i-1}+l_i+dist(r_{i-1},r_i))$$

$$pl_i=\max(pl_{i-1},dist(r_1,r_i)+l_i)$$

$$ql_i=\max(ql_{i-1}+dist(r_{i-1},r_i),l_i)$$

同理令$ST_i$表示环的树$i\sim n$链在一起形成的树(类似于后缀和)，$sd_i$表示$ST_i$的直径，$sl_i$表示$ST_i$中离$r_n$最远的点到$r_n$的距离，$tl_i$表示$ST_i$中离$r_i$最远的点到$r_i$的距离。可以dp：

$$sd_i=\max(sd_{i+1},d_i,tl_{i+1}+l_i+dist(r_{i+1},r_i))$$

$$sl_i=\max(sl_{i+1},dist(r_n,r_i)+l_i)$$

$$tl_i=\max(tl_{i+1}+dist(r_{i+1},r_i),l_i)$$

合并答案：如果你删除的边就是$(r_1,r_n)$，那么答案显然地是$pd_n$。否则假设你删除$(r_i,r_{i+1})$，那么答案就是$\max(pd_i,sd_{i+1},pl_i+sl_{i+1}+w)$。其中$w$表示边$(r_1,r_n)$的边长。

时间复杂度：$O(n)$。

lmxyy讲了一个$O(n\log n)$的做法也很巧妙：倍长环，变成求一个长度为$n$的区间，$pre_i-pre_j+l_i+l_j$的最大值，然后可以直接用线段树维护。(看上去没有比$O(n)$做法慢多少)

【sleep】

从高到低按位确定，攻击数的那一位能为0就为0。

【forest】

一张无向图，每条边有两个权值\(a\)和\(b\)。一条路径\(p\)的长度定义为\(\max_{e\in p}a_e+\max_{e \in p}b_e\)。求\(1\)到\(n\)最短路的长度。

考场上我发现这是边上带权的LCT的时候。。。知道是这个但不会写怎么办啊。。。后来听说只要在每条边的中间加一个点，把边权放到点权上面去就行了。。。

具 体说吧。假设\(\max_{e\in p}a_e=A\)，那么\(\max_{e \in p}b_e\)就是\(a_e \ge A\)的边\(e\)以\(b_e\)为权组成的图的最小生成森林中\(1\)到\(n\)路径上的边权的最大值。想象一下\(A\)不断减小。那么这张 图中的边会越来越多。每加入一条边\(u,v\)，我们就做如下事情(以下“权值”均指\(b\))：

如果\(u\)和\(v\)不连通，那么\(link(u, v)\)；

否则

找到\(u\)和\(v\)之间权最大的边；

如果这条边的权值大于待加入的边的权值，那么cut这条边并\(link(u,v)\)。

LCT维护即可。

后面那几个根号算法完全没有听懂的样子。。

【game】

一个包含了很多内容的提交答案题。

point 1直接手玩即可。

point 2和point 5可以使用随机大法好。具体地说，每次随机一条序列然后把它消除，多做几遍即可得到理想的分数。

point 3和point 4就是检验你会不会miller-rabin。每次随机一条长度为$18$的序列直到其长度为质数，随$1000$次即可。

point 6和point 7也是送分点。搜索即可。注意是从中间往两边搜。

point 8是$a_{i,j}=[(i+j)\equiv 1(\text{mod }2)$的点，夹杂少许噪音。强制不经过噪音，长度为奇数即可。不过这个点我只搜出了7分。

point 9的每一行都是对称的。当然也夹杂了少许噪音。搜索左半边不允许经过噪音，再对称出右半边即可。这个点我也只搜出了7分。

point 10实际上是$37$个$3\times 21$的网格拼起来的，每个网格长得一样且存在回文Hamilton路。

1 2 1 2 3 2 3 4 3 4 5 4 5 6 5 4 5 4 3 4 3 2 3 2 1 2 1
4 3 2 5 4 3 6 5 4 7 6 5 8 7 6 7 6 5 6 5 4 5 4 3 4 3 2
5 4 3 6 5 4 7 6 5 8 7 6 9 8 7 8 7 6 7 6 5 6 5 4 5 4 3

爆搜这个$3\times 27$的表格即可。

终于做完了～做不到满分，只能做出94分。。。算是A了吧，实在做不动了。

【zoo】

跪求\(O(nL)\)算法。

很容易发现next数组构成一棵树，于是我们要求每一个点\(i\)到根的路径中，编号不超过\(\frac{i}{2}\)的点的个数。

我用的是\(O(nL\log L)\)的倍增，常数小所以过了。

常数小在哪里呢?

我一般用\(f[i][j]\)表示点\(i\)走\(2^j\)次方走到的点。改成\(f[j][i]\)之后就快了几倍。

【random】

这题的暴力居然是\(O(nm)\)的。考场上我写数据结构写得要死。。。

【ticket】

一个很显然的dp方程。

设\(x_i\)为\(i\)到根的距离，\(y_i\)为\(i\)走到根的最少资金，那么

\(y_i=\min_{j}{y_j+(x_i-x_j)p_i+q_i}\)

其中\(j\)是\(i\)的祖先。且\(x_i-x_j\le l_i\)。

其实说白了就是求\(i\)的距离不超过\(l_i\)的祖先\(j\)中，\(y_j-p_ix_j\)最大的\(j\)是哪个。如果可以快速求出来的话，这道题就可以做了。

假 设\(i\)的所有满足条件的祖先\(j\)，我们把\((x_j,y_j)\)当成平面上的一个点。再令\(k=p_i\)，那么我们询问的就是让 \(b=y_j-p_ix_j\)最大的点。也就是经过这个点的斜率为\(p_i\)的直线\(y=p_ix_j+b\)截距最大。如果我们能得到祖先上 所有点的凸包，这题就解决了！

可是我不是数据结构魔王，我不会可持久化凸包T_T

vfk的做法：点分治。“先做父亲子树，然 后用父亲子树更新儿子子树”。大致是cdq分治的树上版？按照\(x_a-l_a\)给\(i\)儿子子树内的所有\(a\)排序。然后插入点到凸包内： 由于插入点的横坐标单调递减，所以插入是很简单的。然后还有询问。用set搞搞就行了。

计算几何写得想吐。

给考场上AK的跪了。

这题少一个eps就是10分啊。

。。。

另外挺想知道linux下用lemon评测的时候如何开无限栈？

【prog】

不会捉爆零了>_>

【manager】

树链剖分出来的dfs序把每个子树分成$O(1)$个区间，把每条链分成$O(\log n)$个区间。

所以链剖+线段树即可。

【dinner】

假设从一堆数中选两个集合要求不同集合中的数互质，求方案数。

$f_{i,s_1,s_2}$表示选到了第$i$个数，两个集合拥有的质因子集合分别是$s_1,s_2$的方案数。

对于所有质因子都不超过$19$(还是$23$，反正是调参的问题)的数组成一个集合并dp，复杂度$O(3^8\times n)$。

对于剩下的数，每个数都至多有一个“大质因子”($>19$的质数)，2的多少次方枚举拥有相同”大质因子“的数是否被选，更新dp数组即可。

【epic】

好像这题坑掉了一些人T_T

包括clos。。。

感觉哈夫曼树是冷门算法吧为什么大家都会啊= =

寿司晚宴这种乱搞题都只有三十多个人A，这个题有80+

【savour】

后缀数组模板题，height分组。

【farm】

第一问是水水的dp，$f_i$(前一步不是左/右)和$g_i$(前一步没有限制)表示到达$i$时候经过的最多的树(包括$i$)。$f$的转移只有$O(n)$种，怎么转呢map大法吼；$g$首先是等于$f$，然后枚举前一步是左还是右，如果一棵许愿树是同一行的左起第$k$个，那么它前一步是右的答案是$f_x+k-1$，其中$x$是该树左边$f$值最大的那棵树。

对于不同行的，先算下面的再算上面的；对于同一行的先把$f$都算出来再处理前缀/后缀max来算$g$。(最好记录一下前缀/后缀max吧，方便后面输方案)

把第三问构图改一下就是第二问的答案了。下面考虑第三问，首先我们需要求出所有可能的最优路径然后做最小可重边覆盖。考虑求出所有到达$i$的最优路径：

$solve(i,j)${//$j$是$f$或$g$中的一个，参考上面的定义。

• 如果$vis[i][j]=1$那么return，否则$vis[i][j]\leftarrow 1$；
• 考虑所有能以最优解转移到$i$的、在$i$底下($j=f$时考虑同一行)的点$k$，$solve(k,f+g-j)$

然后构出图之后考虑$S$对每个点连一条边，每个点对$T$连一条边，新连的边流量上界为$1$还是$+\infty$(貌似都可以)，原图中的边流量下界为1。求$S-T$最小流即可。现在复习带下界最小可行流。

(本题不用上下界也是可以做的 但是为了防止以后出题人丧病我还是学一发)

我们先求一个可行的无源汇流$F$，在求之前我们连接边$e'=(T,S,cap=+\infty)$，这条边中的流量代表原图中$F$的流量。

流：一个关于边的函数$f$，满足：

1. $$b(i,j)\le f(i,j)\le c(i,j)$$
2. $$\sum_vf(u,v)=\sum_vf(v,u)$$

(以下采自参考资料[6])令$f(i,j)=b(i,j)+g(i,j)$，那么条件可以改写为：

1. $$0\le g(i,j)\le c(i,j)-b(i,j)$$
2. $$\sum_vg(u,v)+\sum_vb(u,v)=\sum_vg(v,u)+\sum_vb(v,u)$$

于是每条边的上界用$c-b$代替，在新图中的流量就是原图中的流量减$b$。同时新建超级源$S'$和超级汇$T'$，对于每个点$u$，连两条边$(S',u,cap=\sum_vb(v,u))$与$(u,T',cap=\sum_vb(u,v))$(其实这两条边中只需要连一条)。

求出了一个新的图，求它的$S'-T'$最大流。最大流的意思是满足尽量多的下界限制；当然要满足全部的下界限制才能得到合法解，所以有合法解$\Leftrightarrow$满流。

为了构造合法解我们删掉$S',T',e'$，并将所有边的流量加上其$b$。这就得到了一个合法的$S-T$可行流。

然后如果你要求$S-T$最大流的话做几遍dinic即可，当然增广的时候还要考虑反向边流量不能超出下界。(我猜我noi的时候就是错在这里)

这里求$S-T$最小流就是求$T-S$最大流。。就可以了。

参考资料(orz):

[1]byvoid的NOI2009题解

[2]http://blog.csdn.net/pouy94/article/details/5917209

[3]2008论文：周冬《两极相通——浅析最大—最小定理在信息学竞赛中的应用》

[4]http://blog.csdn.net/whjpji/article/details/7547544

[5]http://blog.csdn.net/whjpji/article/details/7547159

[6]2004作业：周源《一种简易的方法求解流量有上下界的网络中网络流问题》

[7]http://blog.csdn.net/jarily/article/details/8591402

[8]https://zh.wikipedia.org/zh/%E9%9C%8D%E5%A4%AB%E6%9B%BC%E7%BC%96%E7%A0%81

(我是翻墙狗)