TC乱刷

都是指div 1。

题解

【SRM593】

250.答案不会超过$3$，特判$0$和$1$的情况，$2$的情况写一个二分图匹配就好。复杂度$O(n^2)$，不要像我一样连单向边FST三次。

450.设A队中动物的$A$的和为$A_1$，$B$的和为$B_1$，总共$A$的和为$A_S$，$B$的和为$B_S$，那么你需要最小化$\max(|A_S-A_1-B_1|,|B_S-A_1-B_1|)$，dp出哪些$A_1+B_1$是可能的。复杂度$O(n^2\times 10000)$。

【SRM246】(这一场好像特别水)

250.→_→

500.你tm在逗我，$O(1000len)$简单暴力，为什么不放到div2的250啊。

1000.第一眼水题。。枚举$i\le D$。。FST了才知道这题的意义→_→比较的时候不要用实数跟实数比较，因为绝对误差可以到$10^{-12}$，long double都hold不住。

【SRM675】

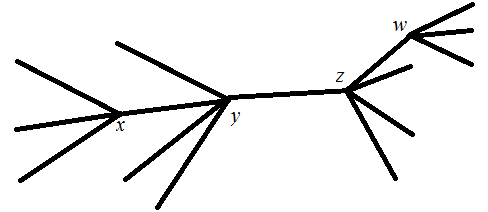
300.我用的是奇怪的构造。。设$x,y,z,w$四个点的度数为$X,Y,Z,W$，那么路径条数为$XY+YZ+ZW$。枚举$X,Y,Z,W$，总是可以在玄学时间内出解。

500.对每个询问从高到低逐位(二进制位)确定答案，即把询问写成“二进制前$i$位为$h$的数中的第$k$大”，每次跑一遍数组更新$h,k$($i$反正就是减$1$)。最后答案就是$h$。

900.

这种题居然不是1000。。令人感动

看着myy的代码大概想到了什么。。%%%myy

首先计算面积的方法是这样的，对多边形(交集)的每一条边，把它跟原点连边形成三角形，把有向面积加起来。所以问题变成了找出所有可能在交集中的边及它们在交集中的概率。如图我们枚举边RS，求出它的出现概率乘上$\Delta RST$的有向面积就能得到它对答案的贡献。

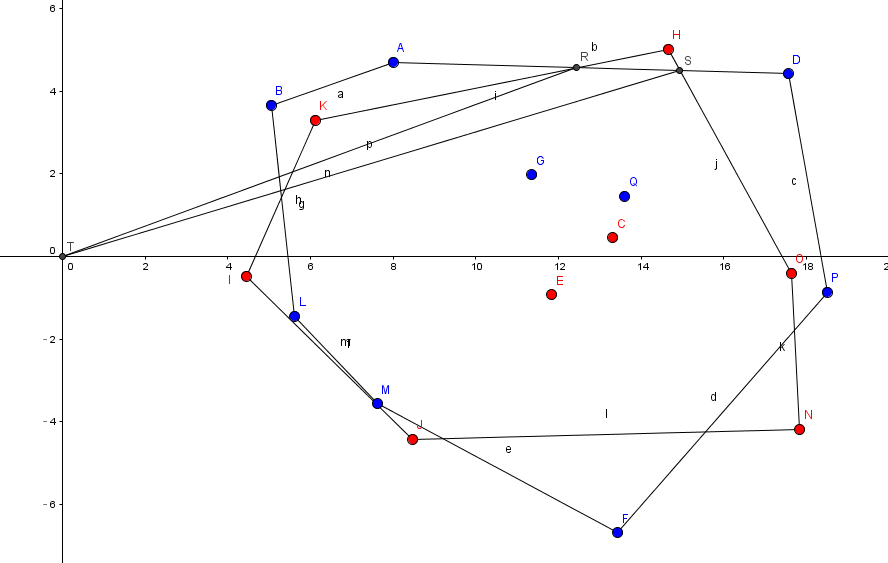
可能的边数不多。它一定是某两个同色点的线段上的一部分。先枚举这两个同色点，假设为$A,D$，都是蓝色。再假设整个蓝色凸包都在下面(站在$A$往$D$看的右边)。那么找出上面的所有点，它们都在红色凸包里。枚举下面的所有点，例如$I$，假设它在红色凸包上且与上面某个点在凸包上相邻。对于一个点$I$定义它的$l$值为它到上面所有点的连线中，和$AD$交点最靠左的那个点到$A$的距离除以$AD$的距离。例如，$l_K=\frac{|AR|}{|AD|}$。如果交点在$A$左边那么$l=0$；如果在$D$右边那么$l=1$。那么$I$左边($l<l_i$的所有点)都是蓝色的，如$B$；同理枚举最右边的$O$，它更右边的点都是蓝色的(如$P$)(右边的定义与左边的略不同，令点的$r$值为最靠近$D$的那个交点到$D$的距离与$AD$的比值，右边是$r$更小的点)。

这样我们得到了一个$O(n^4)$的算法，应该是可以通过本题的。具体地说，首先枚举$A,D$(有顺序。站在$A$往$D$看)及$AD$的颜色(下面假设蓝色)，再枚举下面的所有点对$I,O$，要求$l_I+r_O<1$，算出$R,S$两个点得到贡献；算出$I$左边、$O$右边所有点都是蓝色，$I,O$是红色的概率得到总概率，这个可以$O(n^2)$预处理。

【SRM674】

500.如果原来$i$的排名是$j$，那么无论什么时候$i$的排名都是$j$。如果原来有一辆车向左(右)在$x$位置，那么$t$时间有一辆车在$x-t$($x+t$)位置。所以二分两个数组的第$k$大，用UR4的元旦激光炮的做法就好。

【SRM628】

250.枚举$d$。$d\le 64$。

500.答案是某些电阻的和。假设确定了答案中电阻的个数，那么贪心选最大的几个就好。电阻形成二叉树的关系，用$f_i$表示子树$i$中选一些电阻最多选多少个，那么$f_i=f_l+f_r$(A类)，$f_i=\max(f_l,f_r)$(B类)，$f_i=1$(X类，即叶子)。然后搞出前$f_i$个就好。

1000.

$x,y$代表$0.001X,0.001Y$，即对应的概率。这里的$m$是题目中的$m-n$。

最优决策：先把所有游戏都玩通关(第一轮)，然后选一些游戏玩到2星(第二轮)。那么我们需要求出第一遍的期望时间(所有的$\frac{1} {x+y}$加起来)、第一遍就玩出$\ge m$星的概率，以及对于每个$n\le i<m$，第一遍玩出$i$星的概率乘以补上$m-i$星的期望最优耗时。

我们知道把一个游戏玩到2星的期望时间是$\frac{1}{y}$。。按$y$升序排序，第一遍没有玩到$m$星那么第二遍一定按照这个顺序玩没有到2星的。

对于第$i$关求出它在第二轮中花费了时间的概率，乘上$\frac{1}{y_i}$就是它对答案的贡献。概率就是，第一轮它只拿了一颗星，且它后面拿了两颗星的关卡$\le m+i-n$个。$f_{i,j}$表示后$i$关中一颗星的关卡有$j$个的概率。

复杂度$O(n^2)$。