平面图完备匹配计数
看到绿色夹克衫大爷[5]研究过这个东西。。就来玩了一发。。觉得这个居然可以在多项式时间做出来。。优美啊
复杂度应该是$O(n^3)$乘高精度。。模意义的话不一定资瓷,因为要开方
这篇文章基本上是[1]的一个翻译。。不能算翻译吧因为不是严格一句一句翻的,但是大概就是把[1]用中文说了一遍owo
有一些证明[1]中没有给出,其中Muir的定理证明和Kasteleyn定理的引理1证明是我自己证的,其他的都是搬运。可能各种地方不够严谨、表述不清什么的。。请不吝提出,欢迎打脸。。
以及。。这些算法我都完全没有实现过。。真·嘴巴选手
给出图$G=(V,E)$,求$G$的完备匹配数。
在图是一般二分图的情况下,这相当于求一个矩阵的积和式,而这个问题是#P-Complete的。也就是说目前还没有多项式算法。
然而图是平面图的情况下这个问题有一个$O(n^3)$的算法。
(顺带一提,网格图匹配计数有一个$O(nm)$的公式[4],只是用到了$\cos$函数,需要手写泰勒展开啥的。。不论如何比$O(n^3m^3)$不知道高明到哪里去了)
一些概念
反对称矩阵[6]
满足$A^T=-A$的矩阵(即$A_{i,j}=-A_{j,i}$,$A_{i,i}=0$的矩阵)。
$PM(n)$
把$n$个元素划分成两两一组的所有方案的集合。例如$PM(4)=\{\{\{1,2\},\{3,4\}\},\{\{1,3\},\{2,4\}\},\{\{1,4\},\{2,3\}\}\}$。对于$PM(n)$中的一个元素我们用排列的方式记录它。即:排列$(\alpha_1,\alpha_2,\dots,\alpha_n)$,其中$\alpha_1<\alpha_3<\dots<\alpha_{n-1}$,$\forall i,\alpha_{2i-1}<\alpha_{2i}$,且$\forall i$,$\alpha_{2i-1}$与$\alpha_{2i}$配对。这样$PM(n)$的元素都可以看成排列。
当然$PM(n)$的元素也可以看成无序二元组的集合。。就是说$(i,j)\in \alpha$表示$\exists p,\alpha_{2p-1}=i,\alpha_{2p}=j$或$\alpha_{2p-1}=j,\alpha_{2p}=i$。
Pfaffian[2]
给出一个$2n\times 2n$的矩阵$A$,这里只考虑反对称矩阵的情况,定义
$$\text{pf}(A)=\sum_{\alpha\in PM(n)}\text{sgn}(\alpha)\prod_{(i,j)\in \alpha}A_{i,j}$$
$PerfMatch(G)$
现在我们要求的东西其实是:
$$PerfMatch(G)=\sum_{\alpha\in PM(n)}\prod_{(i,j)\in \alpha}G_{i,j}$$
其中$G$是某平面图的邻接矩阵。
边的定向
对于一个无向图我们把每条边$(i,j)$都替换成有向边$i\to j$或$j\to i$中的一种。这样给出的图邻接矩阵是一个反对称矩阵$A(A_{i,j}=1\text{ when }i\to j,A_{i,j}=-1\text{ when }j\to i)$。
如下图,右边的有向图是左边有向图的一种可能的定向。
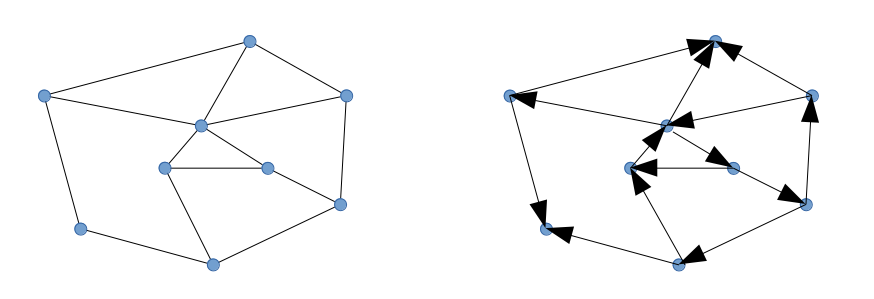
Pfaffian orientation
对于一个定向的邻接矩阵$A$如果有$\text{pf}(A)=\pm PerfMatch(G)$,那么说这是一个pfaffian orientation。(有什么用呢?因为$\text{pf}$很好求啊)
这意味着,对任意$\alpha\in PM(n)$,如果$\alpha$是图的一个完备匹配,则
$$\prod_{(i,j)\in\alpha}A_{i,j}=\text{sgn}(\alpha)\times s$$
其中$s=\pm 1$是与$\alpha$无关的常量。
平面图的面
不解释。
nice cycle
cycle指的是平面图的一个圈(可能包含若干个面)。nice cycle指的是这样的圈:它的长度为偶数,且把它以及它内部的所有东西(点,边)删除之后$G$仍然存在一个完备匹配。
举个例子好了,图来自[1],蓝色圈圈就是一个nice cycle,因为把它删除之后图变成一条长度为$4$的链,显然有完备匹配。
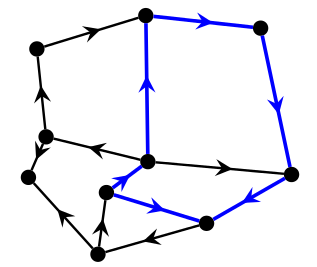
oddly oriented
这个定义只适用于长度为偶数的圈。一个长度为偶数的圈是oddly oriented的,当且仅当这个圈的每个方向(顺时针、逆时针)的边都有奇数条。
“边的定向”那个示例图片中,最外面那一圈是oddly oriented的。“nice cycle”的示例图片中,蓝色圈圈也是oddly oriented的。
一些定理
Muir,1882
令$A$为一个反对称矩阵,则$\text{pf}(A)^2=\text{det}(A)$。
看起来有点玄乎。。举个例子
考虑$4\times 4$的矩阵
$$\left[\begin{matrix}
0 & a & b & c\\
-a & 0 & d & e\\
-b & -d & 0 & f\\
-c & -e & -f & 0\\
\end{matrix}\right]$$
可以暴算得到其行列式为
$$a^2f^2+b^2e^2+c^2d^2+2acdf-2abef-2bcde$$
其pf值为$af+be-cd$。暴算即可验证$N=4$的时候结论成立。
现在开始证明Muir的定理:
证明:我们要证的就是
$$\sum_{\alpha\in PM(n)}\sum_{\beta\in PM(n)}\text{sgn}(\alpha)\text{sgn}(\beta)\prod_{(i,j)\in\alpha}A_{i,j}\prod_{(i,j)\in\beta}A_{i,j}=\sum_{\gamma\in S(n)}\text{sgn}(\gamma)\prod_iA_{i,\gamma_i}$$
然后我们考虑一个$\gamma$,如果它有长度为奇数的循环,那么
- 这个循环长度为$1$,则$\exists i,\gamma_i=i$,而$A_{i,i}=0$。故它对右边不产生贡献。
-
否则找出长度为奇数的、包含的最小数最小的那个循环并把它倒过来(求逆元),记这样的变换为$rev$。即:设$\gamma=\sigma_1\sigma_2\dots\sigma_q$,其中$\sigma_i$是循环,且$\sigma_i$中最小数小于$\sigma_{i+1}$中最小数。记最小的$i$满足$|\sigma_i|\equiv 1\pmod 2$,则$rev(\gamma)=\prod_{j\ne i}\sigma_j\times (\sigma_i)^{-1}$。
然而$rev(rev(\gamma))=\gamma$,$\text{sgn}(\gamma)=\text{sgn}(rev(\gamma))$,且$\prod_iA_{i,\gamma_i}=-\prod_iA_{i,rev(\gamma)_i}$。
所以有奇数个循环的$\gamma$的总贡献是$0$,因为有长度为$1$的循环节的$\gamma$贡献是$0$,否则$\gamma$的贡献与$rev(\gamma)$的贡献抵消。
剩下的$\gamma$就是所有循环节长度都是偶数的排列(这些$\gamma$的集合记为$S_e(n)$)。事实上这种排列的数目就是$|PM(n)|^2$。我们可以构造出$S_e(n)\to PM(n)\times PM(n)$的一个一一映射。
首先,一个$\gamma\in S_e(n)$可以画成若干个环,每个环都是有向的。比如说$\gamma=(1\ 3\ 2\ 6)(4\ 9)(5\ 10\ 7\ 8)$,如下左图。

然后,对于轮换$(a_1 a_2 \dots a_k)(k>2)$,在$\alpha$中拆成$(a_1,a_2),(a_3,a_4),\dots$等匹配,在$\beta$中拆成$(a_2,a_3),(a_4,a_5),\dots$等匹配。这里要求$a_1$是轮换中最小的数,这样$\alpha$和$\beta$是唯一的。
对于长度为$2$的轮换$(a b)$,$\alpha$和$\beta$中都有$a,b$配对。
上面那个图中间是$\alpha$,右边是$\beta$。
这是一个一一对应。因为它的逆映射就是把两个匹配拼在一起,形成若干个环,给环定方向的时候按照“环中最小的点连向其在$\alpha$中的匹配点”来定。记这个一一对应为$\varphi$。
我们证明引理1:$\varphi(\gamma)=(\alpha,\beta)$,那么$\text{sgn}(\gamma)\prod_{i=1}^n(-1)^{[\gamma_i<i]}=\text{sgn}(\alpha)\text{sgn}(\beta)$。
因为$(3\ 4\ 1\ 2)$是偶置换,所以置换$a$的奇偶性只与有序二元组的无序集合$\{(a_1,a_2),(a_3,a_4),\dots,(a_{n-1},a_n)\}$有关。那么我们不用在意$\alpha_{2i-1}<\alpha_{2i+1}$这样的奇奇怪怪的限制了。
在计算$\varphi$映射的时候,我们先找出$\gamma$的所有环(轮换),对每一个环将边交替地放入$\alpha,\beta$。对于一条边$(i,\gamma_i)$,如果$\gamma_i<i$,那么$\alpha$或$\beta$中的顺序是$\gamma_i,i$;否则是$i,\gamma_i$。然后对每个$\gamma_i<i$的$i$交换$i$和$\gamma_i$在对应的$\alpha$或$\beta$中的位置。这样$\text{sgn}(\alpha)\text{sgn}(\beta)$改变了$\prod_{i=1}^n(-1)^{[\gamma_i<i]}$,且$\alpha$或$\beta$中每一个二元组都是形如$i,\gamma_i$的形式。这样可以认为$\gamma$中的一个轮换是$(i_1\ i_2\ i_3\dots i_k)$,此时$\alpha$中对应的位置是:
$$i_1\ i_2\ \dots\ i_k$$
而$\beta$中对应的位置是:
$$i_2\ i_3\ \dots\ i_1$$
所以这几块对$\text{sgn}(\alpha)\text{sgn}(\beta)$的贡献是把$i_1\ i_2\ \dots\ i_k$变成$i_2\ i_3\ \dots\ i_1$需要的对换数,即为$k-1$。而$k-1$是奇数。
所以$\text{sgn}(\alpha)\text{sgn}(\beta)\prod_{i=1}^n(-1)^{[\gamma_i<i]}$是$(-1)$的$\gamma$的轮换的个数次方。而$\gamma$的轮换长度都是偶数的,所以上述式子就是$\text{sgn}(\gamma)$。
引理1得证。由引理1可以得到每个$\gamma$对行列式的贡献等于$\varphi(\gamma)$对$\text{pf}^2$的贡献。本定理得证。
Kasteleyn,1963
每个平面图$G$都存在pfaffian orientation,且可以在多项式时间内找到它。
证明:
考虑如下算法:
- 找出$G$的一个生成树$T_1$
- 给$T_1$的边随意定向
- 考虑不在$T_1$中的所有边,它们在对偶图中对应的边构成了对偶图一棵生成树$T_2$
- 从$T_2$的叶子开始可以递推出不在$T_1$的所有边的方向。递推的规则是:每个面都有奇数条边是顺时针的。
- (如下图,红色粗线是$T_1$,蓝色是$T_2$,红色细线是后来递推出的方向)
- (图来自[1])
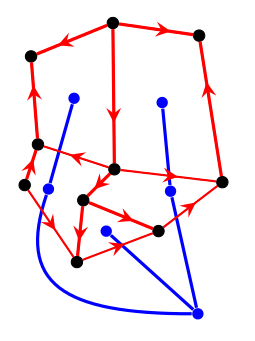
它显然是个多项式算法。
为了证明这个定向是pfaffian的,我们需要这两个引理:
-
如果每一个nice cycle都是oddly oriented,那么这个定向是pfaffian的;
证明:
先分析分析。$s=1$的pfaffian orientation等价于对每一个完备匹配$M\in PM(n)$,$M$的逆序对数与如下数字同奇偶:$M$中的每一对$a,b(a<b)$,如果这条边在定向中是$b\to a$,那么加$1$。$s=-1$等价于这两个数不同奇偶。
换句话说,一个定向是$s=1$的pfaffian orientation,当且仅当对于所有完备匹配$M$,把$M$中的二元组$a,b$按照定向的顺序写下来(如果图中的边是$a\to b$,那么顺序是$a,b$,否则是$b,a$),得到一个排列,其逆序对数都是偶数。$s=-1$的情况即逆序对数是奇数。
我们考虑这样得到的任意两个排列$\alpha,\beta$,满足$\forall i,(\alpha_{2i-1}\to \alpha_{2i})\in E,(\beta_{2i-1}\to \beta_{2i})\in E$。只要证明了$\text{sgn}(\alpha)\text{sgn}(\beta)=1$,就可以证明原命题。
我们知道两个匹配拼在一起就是一些长度为偶数的圈。考虑其中一个圈$C$,顶点为$v_1,v_2,\dots,v_{2k}$。首先,$C$是一个nice cycle,因为考虑匹配$\alpha$,删除$C$上的点和边之后显然没问题,$C$内的点不会与$C$外的点匹配(连这样的边都没有),所以删掉$C$和$C$内的东西之后剩下的图还是有完备匹配。
由题设,$C$是nice cycle,那么它是oddly oriented的。
然后假设在$\alpha$和$\beta$中$v_1,v_2,\dots,v_{2k}$都是排在一起的,即$\alpha$中有一个片段形如$v_1,v_2,v_3,\dots,v_{2k}$($v_{2i-1}$与$v_{2i}$的顺序可以调动),同理$\beta$中有一个形如$v_2,v_3,\dots,v_{2k},v_1$的片段。考虑$C$中每条边$(v_i,v_{i+1})$,它一定出现在$\alpha$中或$\beta$中。如果它是$v_i\to v_{i+1}$则不用管;否则我们在对应的排列中(比如,$i$是奇数就是$\alpha$;$i$是偶数就是$\beta$)交换两个元素的位置。现在$\alpha$中有片段$v_1,v_2,\dots,v_{2k}$(顺序就是这样的),$\beta$中有片段$v_2,v_3,\dots,v_1$,且我们一共用了奇数次(因为$C$是oddly oriented的)交换。再通过奇数次交换可以把$v_1,v_2,\dots,v_{2k}$变成$v_2,v_3,\dots,v_1$。所以,一个环对$\alpha\times\beta$的逆序对数的贡献是偶数。
这样就证明了,任意的$\alpha$和$\beta$拥有相同的奇偶性。换句话说,这个定向是pfaffian的。 -
如果一个定向的每个面都是奇数条顺时针的边,那么每个nice circle都是oddly oriented。
证明:
考虑一个长度为偶数的圈$C$,$C$内部有$e$条边,$f$个面,$v$个点,根据欧拉公式有$e=v+f-1$。令$d(face,edge)$表示$edge$这条边在面$face$中的定向,顺时针为$1$,逆时针为$0$;对于在$C$最外圈的边$edge$,令$d(edge)$表示$d(\text{最外圈},edge)$。
那么在模$2$意义下我们有$f=\sum_{face\text{是一个面}}\sum_{edge\in face}d(face,edge)=\sum_{edge\in C\text{的外面一圈}}d(edge)+e$。
这个公式是因为:考虑$edge$,如果它在外面一圈上,那么它的贡献是$d(edge)$;否则它的贡献就是$1$(它被算了两个面,一个面是顺时针,一个面是逆时针)。$f$的组成部分有($e$减去圈$C$的长度)个$1$,因为$C$是偶圈所以模$2$意义下就是$e$个$1$;还有$\sum_{edge\in C\text{的外面一圈}}d(edge)$(记这个量为$S$好了)。即$f=e+S$。
再考虑欧拉公式就有$v+S-1=0$。然而$v$是偶数(因为$C$是nice cycle,去掉它之后图有完备匹配,点数显然是偶数),所以$S$就是奇数咯,那么$C$就是oddly oriented的啦。
Q.E.D
算法
很简单,求出该图的一个pfaffian orientation之后,$O(n^3)$算出其行列式然后开个根就是答案。由于答案只有指数级(就是说,答案的位数是多项式的),所以只要暴力模拟高精度或写个crt就可以求出答案的精确值,总之一切都是在多项式复杂度内的。
如果是模意义呢。。开根的时候会不会有问题,我还没仔细想。看上去不是很好做?
无论如何这是一个很漂亮的算法。。只是开根那里有点遗憾不知道是否资瓷模意义。
参考文献
- [1] Ashley Montanaro,"Counting perfect matchings in planar graphs"
- [2] wikipedia,Pfaffian
- [3] wikipedia,FKT algorithm
- [4] wikipedia,Domino Tiling
- [5] 51nod
- [6] wikipedia,Skew-symmetric Matrix
绘图 by LibreOffice Draw,有一些图片是直接从[1]中截的。
nonsense
能发现白字的都是神犇啊
扯下淡。。你问我这玩意在OI中有什么用。。显然没用啊
我更愿意把计算机科学看成数学的一部分?
唔。。换个话题。。GFW好像又变厉害了,现在l5n都挂掉了,想去twitter上写一些真正的废话也去不了
祝高考党们都能成功。。
祝thusc、pkusc大爷们都能拿到自己喜欢的协议。。
还有窝最近那场51nod弃疗了。。窝发现窝真的不适合手速场啊QAQ
就酱
哦对了,这是我第一次用jQuery写博客,那几个按钮啥的都是jQuery的简单应用
其实一开始要我学jQuery的时候,我是拒绝的。。但是这玩意太tm漂亮了
不过不会jQuery的话写网页就会混不下去?我猜的
你能看到这里才是真的神犇
组织又要出新歌了。。好像完全换了个风格。。(吸毒神曲

我就知道这种名字是写不出歌的(坐等打脸)
果真曲子改名了。。
从30s预览中可以听出,应该是吃货歌
以及根本听不出歌词是什么鬼嘛,只听出了Burry,Cherry(坐等打脸)
 评论 (0)
评论 (0)