codechef JUNE16

这个月题目难一些啦

主要是因为mgch出的凸包题以及sereja的逃离

按照我做题的顺序写好了。。这次我顺序有点奇怪。。

FRJUMP

只考虑模$10^9+7$，那么相当于每次改变一个数然后询问所有$R$的倍数的乘积

我们改成每次把一个数的所有约数加上多少多少，每次询问就直接搞。约数个数很小了。。虽然是$O(\sqrt{n})$的但是一般达不到呢>_<

复杂度大概是$O(\sqrt{n}Q)$，1s应该不虚吧

然后如果要询问首位数的话。。窝翻了一下stackoverflow，全都在说对数法。。(就是询问对数之和然后exp一下)。。

好像取以10为底的对数最靠谱了。。设对数为$I+f$，其中$I$是整数而$f<1$，那么答案就是$10^f\times 10^I$的首位。。也就是$\lfloor 10^f\rfloor$啦

数据比较小的时候精度比较萎。。数据大的时候就好了(不过如果精心构造数据的话还是能卡掉吧?比如选一个很接近$10^{1000}$的合数，如果它的质因子都很小，就可以拿来卡)

嗯还有一个严重的问题。。就是约数个数的上界到底是多少。。$O(\sqrt{n})$好像很松的样子。。

CHNWGM

令$k$为放下去之后的加分，$h$为放下去之后棋盘的估价值

每次选择使得$h+k$最好的走法

就看估价值$h$怎么算咯>_<

窝瞎写了一个估价值然后弃疗了。。效果大概是最优算法的$\frac{1}{500}$。。不管了

BINOP

and操作就是如果串中有0那么把某个值变成0；or操作就是如果串中有1那么把某个值变成1；xor操作就是交换。

当$A$中所有字符都是同一个且$A\ne B$时答案是Unlucky Chef，否则设有$a$个位置上$A_i=1,B_i=0$，$b$个位置上$A_i=0,B_i=1$，那么答案是$\max(a,b)$。(先把$\min(a,b)$个交换，剩下的赋值)

CHCOINSG

打表发现能输当且仅当$N$是$6$的倍数

如果$N$是6的倍数，那么无论怎么走都不可能走到$N$不是$6$的倍数的情况(否则走的步数是$6$的倍数而不是$p^x$)

如果$N$不是6的倍数，那么总是可以走到$6$的倍数的。。因为1、2、3、4、5都可以走

CHEFARK

假设序列有$0$，有$P$个非$0$数那么答案显然是$\sum_{i=0}^{\min(K,P)}\binom{P}{i}$

假设序列没有$0$那么答案是$\sum_{i=0}^{\min(K,N)}[i\equiv K\pmod 2]\binom{N}{i}$

DEVARRAY

→_→，直接把数组最大最小值搞出来看询问值是否在这个区间内就好

CHEARMY

重新看了一下题目发现是子序列不是子串

就是说所有数字都是偶数

(因为这玩意显然等于$\prod (1+a_i)-1$，其中$a_i$是第$i$位，减去那个$1$是空序列

转成五进制每个数位乘2再转成十进制就是了

现在的cc真是世风日下，普及组的题(noip2006 T4 序列 sequence)改一改就能出了

CHSQARR

什么鬼翻译。。增加1变成了减小1害的我过不了样例

一次询问$O(NM)$做即可。枚举所有可能的长方形，和很容易算，但是关键是$O(1)$求最小值。如果用二维st的话预处理是两个log的会狗带。

先对每一列搞一个st表，这样可以$O(1)$查询列最小值。。然后枚举行的时候搞出所有列最小值然后相当于选一个固定长度的区间使得min值最小，单调队列瞎搞搞就是。

复杂度$O(NM\log N+QNM)$

或许不需要st表，只需要两维单调队列?没仔细想。。不过复杂度瓶颈是$QNM$吧。。再说了有4s时限嘿嘿嘿

SADPAIRS

对于一个连通块：首先tarjan一波，搞出所有low、dfn和割点。

然后枚举颜色$c$，我们需要对每个点求出割掉它之后这个连通块内有多少对颜色为$c$的点对不再连通。割掉一个割点$x$的话图会分裂成这么些连通块：dfs树中如果$c$是$x$的儿子，且$low_c\ge dfn_x$那么$c$会被分离出去。

考虑构造该颜色的所有点的虚树(窝不是不会写虚树吗)，就可以计算该颜色对所有点的贡献了。具体地说：

对于一个在虚树中的点$x$，枚举$x$在虚树中的所有儿子$c$，找到既是$c$的祖先又是$x$的儿子的那个点$d$，如果$low_d\ge dfn_x$，那么$c$会分裂出去，答案加上$\binom{c}{2}$；否则全局连通块(割掉$x$之后与根相连的那个)的大小$s$加上$c$。最后答案加上$\binom{s}{2}$。

对于一个在虚树中的边$(a,b)$，设$a$所在子树大小为$S_a$，$b$所在子树大小为$S_b$，我们需要考虑这条边在原树中的链上的所有点(不包括$a,b$)的贡献。如果点$x$在链上的儿子$y$有$low_y\ge dfn_x$那么$x$的答案增加$\binom{S_a}{2}+\binom{S_b}{2}$；否则不改变$x$的答案。为了方便我们把答案存在边上，最后统计的时候对所有边如果父亲的dfn不超过儿子的low那么把边的权值加给父亲；这样就变成了一条祖孙链上做加法。

对每个连通块每种颜色做一遍就好，复杂度$O(n\log n)$。

以及这题很恶心。。卡爆栈。。我开始不会求割点，然后统计边上答案那里想错了，虚树写错了几遍，非递归tarjan又写错了。。自己太傻不要怪出题人咯

MGCHGEOM

c站三大镇站之宝：sereja,mgch,pavel1996

所以窝比专家知道得都多些?(雾)

YMDragon神犇有这题的一个做法。。离线$O(n\log^2 n)$，空间$O(n\log^2 n)$。。窝太虚了就没写。。写了个在线的论文算法

论文来自Mark H. Overmars和Jan van Leeuwen的Maintenance of Configurations in the Plane。我把数据结构改动了一下使得这个题好写一些了，我只写了15k。(请配合该论文阅读本题解)

首先需要一种叫concatenable queue的数据结构：有序数组，资瓷一个log进行合并操作和拆分操作。窝用的是splay。顺带一提如果这个数据结构不用splay而是用论文上的啥啥树，复杂度就是在线的严格两个log。(splay是均摊)

然后定义一个凸包的左凸壳是这些点与$(+\infty,0)$组成的凸包。

这种数据结构是用来维护左凸壳的，叶子节点是凸壳上的点，非叶子节点上维护其两旁的点组成的向量。以及我们需要$O(1)$访问一个子树的最左边/最右边的叶子。

然后给出两个左凸壳，保证其中一个的最低点高于另一个的最高点，可以$O(\log n)$求出它们之间那座桥，从而合并这两个凸壳。具体见论文啦，论文分了10种情况讨论，然而其实只要5种(就是去掉了相切的情况)。。补张图，B就是图中两个凸壳的桥。

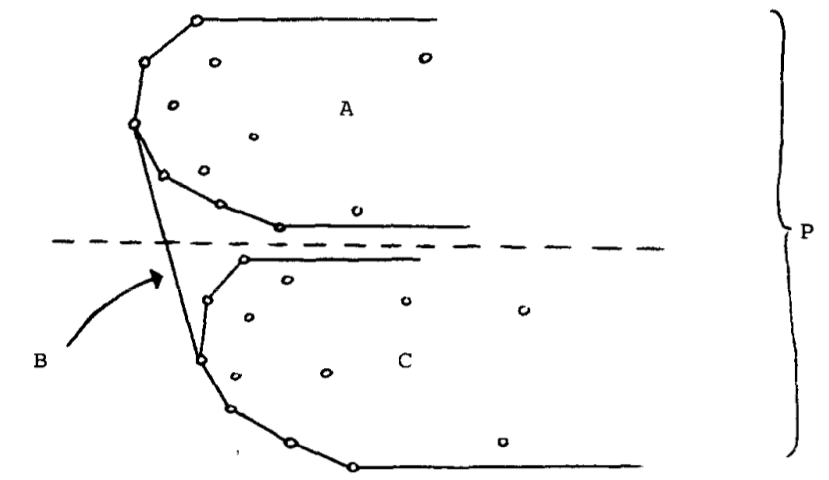
现在用平衡树维护这些点，按照$y$坐标维护，平衡树的叶子节点储存所有点，非叶子节点储存凸壳。对于一个点$x$，设$f(x)$是$x$的父亲，$Q(x)$是$x$中所有点组成的左凸壳，$x$中维护

• 父亲$f(x)$，左儿子$l(x)$，右儿子$r(x)$
• $Q(x)$中不在$Q(f(x))$中的那一段(一定是某开头或某结尾)，论文中记作$Q^*(x)$
• $Q(x)$中在$Q(f(x))$中的点的个数，论文中记作$B(x)$

对于根节点$root$，$Q^*(root)=Q(root)$。

然后就是DOWN过程：DOWN($x$)表示$x$是一棵平衡树的根，执行这个过程之后$x$的两个儿子分别是两棵平衡树的根($x$是根的意思是$Q^*(x)=Q(x)$)。首先把$Q^*(x)$按照$B(l(x))$所在位置断裂，然后跟$Q^*(l(x))$与$Q^*(r(x))$拼起来。如图

注：我写的DOWN和论文中的DOWN不一样。。我的DOWN只改变三个节点，不进行递归。。接下来的UP过程同理。

UP过程相当于DOWN的逆过程。有两棵树$l,r$，$Q^*(l)=Q(l),Q^*(r)=Q(r)$，把它们添加到一个父亲$x$底下，更新这三个点的$Q^*$值和$B$值。

UP的话首先用那个log求桥的办法找到桥。。然后把$Q^*(l)$和$Q^*(r)$在切点出断裂，拼到$Q^(x)$处。下面是论文中的伪代码。

如果要维护平衡树的平衡的话。。旋转前down，旋转完了up就差不多了。

不过如果连续down两遍某个节点或连续up两遍的话，会产生奇怪的后果。。所以维持平衡的部分(我用的SBT，就是maintain过程啦)要想清楚再写。

最后，也是很重要的一点!这个算法不资瓷两个点的$y$坐标相等的情况!我的程序手写了随机扰乱，一个num结构体就是一个数$y+add\epsilon$。令人北上的是，对于$N=2000$，所有坐标在$[-10,10]$内随机的数据，它还是wa了。(嘘，不要告诉mgch)

upd：被我猜中了结局，在比赛还有一个多小时(我还在调mgch题的时候)收到信息比赛延长两天。。这果真是我熟悉的cc。。

updd：我直到比赛结束那天的早上才调出这个题。。浪费了我三天时光。。鈤

nonsense

在写完了10k的mgch题的代码之后还没开调，看到组织出的新歌。。当时我就惊呆了

没搞懂歌词说的是什么。。好像跟bathtub mermaid讲的是差不多的故事。。歌词结构都差不多(雾)

(不过从作曲上看，确实是一首不错的曲子。。从作词上看就是程序员之歌

然后就停止了调试，mgch题狗带了