up-down排列，$\tan$函数，$\zeta$函数与复分析

写在前面

这是我们计算机应用数(fu)学(bian)课程的一个笔记。(对，就是那次上了新闻联播的课程，当时姚老板在黑板上讲复分析，我们一脸懵逼地看着摄像机。。因为我有独特的占座技巧，抢到了一个优秀的座位，全程躲过了摄像机。。室友被给了2s特写，估计是颜值太高了→_→

作为一个工科生(233)，我们当然不会去学那些严谨的复分析。。所以有的东西就是扯扯，然后这个式子可以这样玩，也不管为什么了。这篇文章应该不是很严谨吧。反正只是个复习笔记。不过我尽量做到比较严谨。

不过姚老板确实用两节课就带领我们领略了复分析的一角。。算是很成功地展现了复分析的魅力。(比微积分课不知道高明到哪里去了

引入

先扯点淡。。

一个长度为$n$的排列$p$被称作up-down排列，当且仅当$n$是奇数，且$p_1<p_2$,$p_2>p_3$,$p_3<p_4$,$\dots$,$p_{n-1}>p_n$。求长度为$n$的up-down排列的个数。设为$b_n$好了。

很简单嘛>_<，我们枚举最大的那个数在哪，记做$p_i$，那么$i$显然是偶数。$i$左边和$i$右边是两个up-down排列，且它们不相关联，那么我们分配一些数给左边，一些数给右边就好。也就是说

$$b_n=\sum_{i\text{ is even and }<n}\binom{n-1}{i-1}b_{i-1}b_{n-i}$$

初始条件$b_0=0,b_1=1$，那么所有偶数$n$都满足$b_n=0$，这与题目中的定义是相符的。而且$b_n$的递推式中那个“$i$是偶数”的限制也可以丢掉了。

考虑推这个东西的通项。推通项的一个重要工具就是母函数，这里$b_n$的转移里面有组合数，我们很容易想到指数型母函数$B(x)=\sum_{n\ge 0}\frac{b_n}{n!}x^n$。这样就有

\begin{align*}
B'(x)&=\sum_{n\ge 1}\frac{b_n}{(n-1)!}x^{n-1}\\
&=1+\sum_{n\ge 1}\sum_{i=1}^n\frac{(n-1)!}{(n-i)!(i-1)!}b_{i-1}b_{n-i}\frac{x^{n-1}}{(n-1)!}\\
&=1+\sum_{n\ge 1}\sum_{i=1}^n\frac{x^{n-i}b_{n-i}}{(n-i)!}\frac{x_{i-1}b_{i-1}}{(i-1)!}\\
&=1+(B(x))^2
\end{align*}

使用高超的微积分技巧再代入$B(0)=0$就可以解出$B(x)=\tan x$。那么问题来了：$B(x)$的泰勒展开是什么呢?

复平面

为了解决这个问题，我们把目光投向复平面。先说一下复平面能帮我们干什么吧。

考虑一个函数$f(z)=\sum_{n\ge 0}a_nz^n$。我们现在想求$a_k$。一个天才发现了这样一个规律：令$\gamma$为单位圆，则

$$\oint_{\gamma}z^n\text{d}z=\int_{0}^{2\pi}e^{ni\theta}\text{d}(e^{i\theta})=i\int_0^{2\pi}e^{(n+1)i\theta}\text{d}\theta$$

当$n\ne -1$的时候，上述积分算出来等于$0$；当$n=-1$时上述积分算出来等于$2\pi i$。

考虑沿着单位圆$\gamma$进行如下积分

\begin{align*}
&\oint_{\gamma}\frac{f(z)}{z^{k+1}}\text{d}z\\
=&\sum_{n\ge 0}a_n\oint_{\gamma}z^{n-(k+1)}\text{d}z\\
=&2\pi ia_k
\end{align*}

要求出$a_k$，我们只需要对一个函数沿着单位圆做一次积分就好。

那么就开始研究复平面上的积分吧。

Cauchy's integral theorem

$U\subseteq \mathbb{C}$为单连通开集，对于$U$上的全纯函数$f$，和一条$U$中的封闭曲线$\gamma$，

$$\oint_{\gamma}f(z)\text{d}z=0.$$

一些定义

这个定理说什么呢。。就是函数是全纯的。。那么我们绕着一条封闭曲线走一圈那个积分是$0$。

我们以$\frac{1}{z}$为例，它在下图中$U$上是全纯的，那么对于我们画的曲线，积分就是$0$。

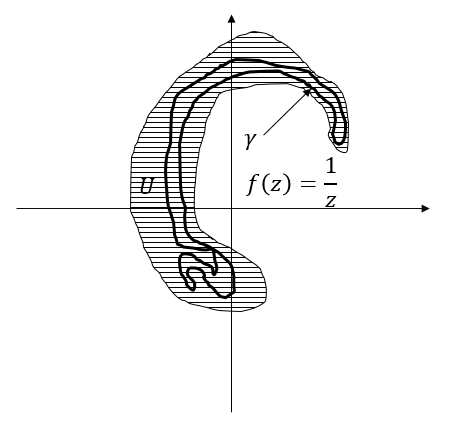
提供两个反例：

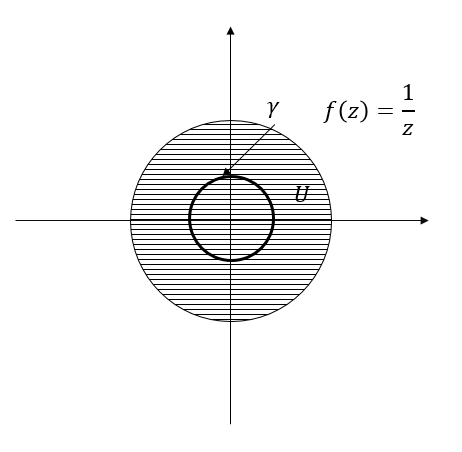
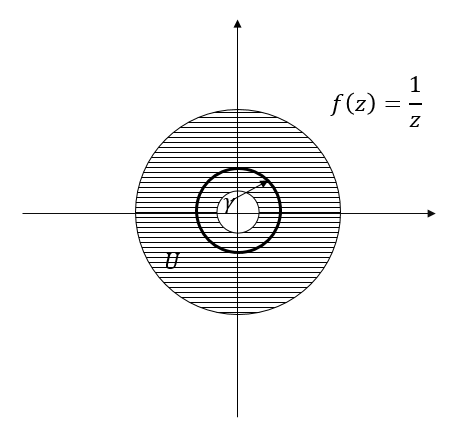
上左图中$f(z)$在$U$上不是全纯(在$(0,0)$处连定义都没有)，上右图中$U$不是单连通，所以上面两个图的$\oint_{\gamma}f(z)\text{d}z$都不是$0$(我们已经知道这个积分是$2\pi i$了)。

Cauchy's residue theorem

我们知道如果曲线内部包含了一些奇点(比如说没有定义或者导数不存在的点)，这个曲线的积分就不一定是$0$。但是我们可以把曲线往里面推或者往外面拉，总之只要中间过程中不经过奇点，那么曲线的积分就不变。大概就像这样(应该是可以严格证明的，但是我懒)：

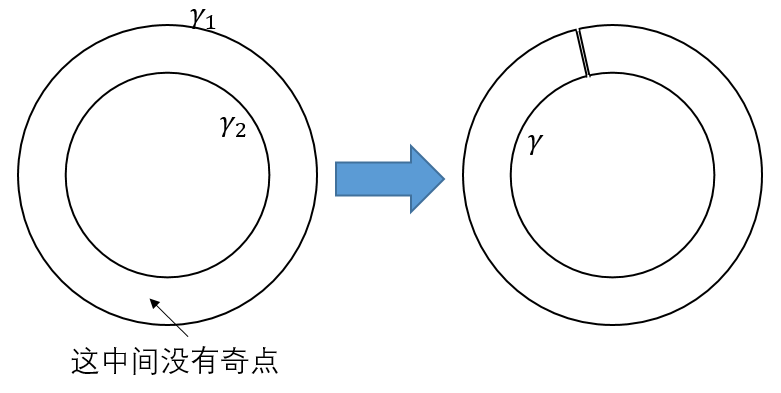
根据Cauchy's Integral Theorem，$\oint_{\gamma}f(z)\text{d}z=0$，那么就可以推出$\gamma_1$和$\gamma_2$这两条曲线的积分是一样的。

如果只有有限个奇点，那么积分变得更加简单：

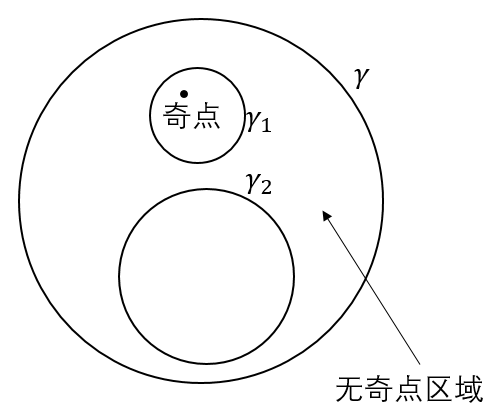
$\gamma$的积分等于$\gamma_1$的积分加上$\gamma_2$的积分。这里$\gamma_1$可以取成奇点为圆心，半径足够小的一个圆。

嗯，把这个过程进行下去，曲线的积分就变成了每个奇点附近的圆的积分加上一个“内部没有奇点的曲线”的积分之和。“内部没有奇点的曲线”积分是$0$，那么曲线的积分就是里面的奇点附近的圆的积分之和。如下图，大圆上的积分，就等于里面几个小圆上的积分的和——这个东西只与奇点有关。

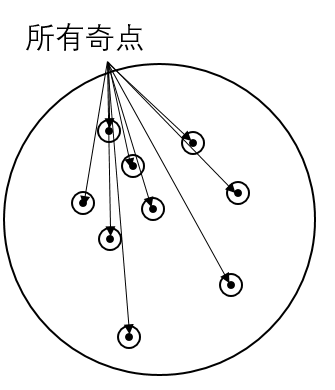
我们只需要对每个奇点求出它附近的小圆的积分，就可以搞定任何曲线上的积分了。

如果函数$f(z)$在奇点$z_0$附近能写成$\sum_{i=1}^m\frac{c_i}{(z-z_0)^i}$加上一个全纯函数，那么根据之前的计算，$\oint_{\gamma}f(z)\text{d}z=2\pi i c_1$，其中$\gamma$是$z_0$附近的小圆。我们把$c_1$定义为$f$在$z_0$处的留数，记做$\text{Res}(f,z_0)$。那么Cauchy's residue theorem可以写成：

$$\oint_{\gamma}f(z)\text{d}z=2\pi i\sum_{k=1}^n\text{Res}(f,a_k),$$

其中$a_1,a_2,\dots,a_n$为$\gamma$内的所有奇点。

求$\tan z$展开式的第$n$项

由up-down排列那部分的讨论，我们可以假定$n$是奇数。

注意到$\tan z=i\frac{e^{-iz}-e^{iz}}{e^{-iz}+e^{iz}}=i(1-\frac{2}{e^{-2iz}+1})$，而且在$\frac{\pi}{2}+p\pi(p\in\mathbb{Z})$处为奇点。那么$f_n(z)=\frac{\tan z}{z^{n+1}}$的奇点除了$0$以外还有这些数。我们发现当曲线取得非常大的时候，曲线上的积分趋于$0$(后面会仔细讲)，换句话说所有奇点的留数和等于$0$。我们只要把$z_k=\frac{k\pi}{2}$($k$为奇数)这一类奇点处的留数求出来就能求出$f_n(z)$在$0$处的留数。根据Wikipedia留数词条的一个公式，

$$\text{Res}(f_n(z),z_k)=\lim_{z\to z_k}(z-z_k)f(z)=\frac{1}{z_k^{n+1}}\lim_{z\to z_k}(z-z_k)\tan z$$

令$w=z-z_k$，则

\begin{align*}
&(z-z_k)\tan z\\
=&wi(1-\frac{2}{e^{-2i(z_k+w)}+1})\\
=&wi(1-\frac{2}{1-e^{-2iw}})\\
=&wi(1-\frac{2}{1-(1-2iw+o(|w|))})\\
=&wi-\frac{w}{w+o(|w|)},
\end{align*}

当$w\to 0$时这个式子趋于$-1$。所以$\text{Res}(f_n(z),z_k)=\frac{-1}{z_k^{n+1}}=-(\frac{2}{\pi})^{n+1}\frac{1}{k^{n+1}}$。

令$C_k$为边平行于坐标轴，经过$k\pi,-k\pi,k\pi i,-k\pi i$的正方形，其中$k\in\mathbb{Z}$，如下图。

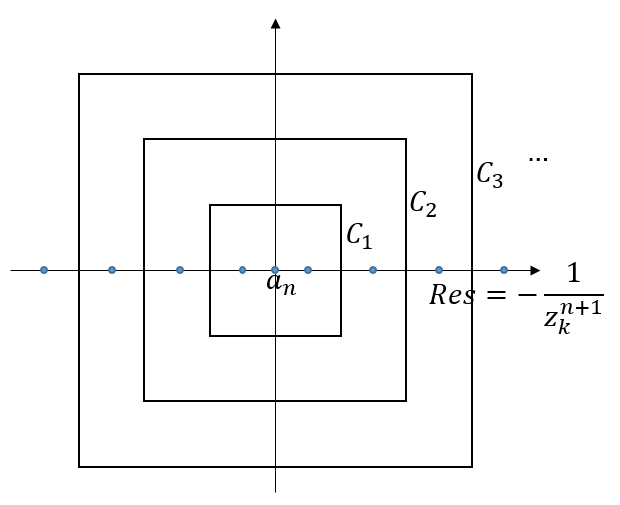
我们可以大致估计$I_k=\oint_{C_k}\frac{\tan z}{z^{n+1}}\text{d}z$的界。考虑$C_k$的右侧那条边，$z=k\pi+yi$，那么$\tan z=i(1-\frac{2}{e^{2y}+1})$，而$y$是实数，那么$|\tan z|\le 3$。考虑$C_k$左侧的边同理。考虑$C_k$上面那条边，$z=x+k\pi i$，那么$\tan z=i(1-\frac{2}{1+e^{-2ix+2k\pi}})$。分母的模长至少是$e^{2k\pi}-1$，那么$|\tan z|\le 1+\frac{2}{e^{2k\pi}-1}\le 3$。下面同理。这样，$|I_k|$至多是曲线长度乘以$\frac{3}{(k\pi)^{n+1}}$，即$|I_k|\le \frac{24}{(k\pi)^n}$。

我们整理一下刚刚说了什么：我们有一族曲线，$C_1,C_2,\dots,C_k,\dots$，$I_k$是$C_k$上的积分，换句话说是$C_k$内的所有奇点的留数之和乘以$2\pi i$。设$R_k$为$C_k$内所有非零奇点的留数之和，$a_n$为$0$处的流留数，那么$\frac{I_k}{2\pi i}=R_k+a_n$。令$k\to\infty$，$|I_k|$趋于$0$，故左边趋于$0$。而当$n$为奇数的时候，$R_k$的极限为$-2(\frac{2}{\pi})^{n+1}\sum_{k\ge 1}\frac{1}{(2k-1)^{n+1}}$。

这里需要说明的是：正半轴和负半轴都有奇点，所以会乘$2$。此外，如果$n$为偶数，那么$\frac{k}{\pi}$和$-\frac{k}{\pi}$处的留数抵消，那么$a_n$直接等于$0$。

而$\sum_{k\ge 1}\frac{1}{(2k-1)^{n+1}}=\frac{2^{n+1}-1}{2^{n+1}}\zeta(n+1)$，其中$\zeta$是黎曼zeta函数。

这给出了$n$为奇数时$a_n$的公式：

$$a_n=2\frac{2^{n+1}-1}{\pi^{n+1}}\zeta(n+1).$$

那么$n$个数的up-down排列的个数为$b_n=a_nn!$，我们就算是求出了$b_n$的通项。

关于$\zeta$函数

用这样的方法就能推出$\zeta(2k),k\in\mathbb{Z}$的值。然而Mathematica并不知道$\zeta(3)$的值——听说到现在仍是个open problem。

(upd：我说的是精确值。近似值早就有人算了→_→

另外，$\tan x$还有一个Taylor展开：

$$\sum_{i\ge 1}(-1)^{i-1}\frac{2^{2i}(2^{2i}-1)B_{2i}x^{2i-1}}{(2i)!},$$

其中$B$是伯努利数。至于这个是怎么推出来的，以及$\zeta$函数和伯努利数之间的关系。。我懒得管啦

最后祝您，身体健康。

(upd:之前把“留数”写成“流数”。。我tm很狼狈啊。。