codechef AUG17
垃圾cha题,毁我青春。以后看到琪琪给给的cha题还是不要去做了吧。。
upd. rating predictor说我7☆了。。那这应该就是退坑一战了吧。。虽然以后还会去cc圈圈钱,我也还会继续爱着这个oj的哦(笑)
RAINBOWA
先判是不是1234567654321形的串,再判是不是回文串。
CHEFMOVR
考虑$D=1$的情况,首先平均数得是整数,然后从左至右每次贪心地将当前数变成平均数即可。
$D\ne 1$的情况,会发现数列中下标膜$D$不一样的数是不影响的,变成$D$个$D=1$的问题做就好。
复杂度$O(N)$。
话说我因为cout和printf混用WA了一发。
GCAC
大模拟
PALINGAM
垃圾讨论题。
第一步A出的字符B必须没有,否则B胜。
如果第一步A出的字符为$c$,且$c$在$s$中的出现次数至少为$2$,那么A胜。
第二步B出的字符$d$A必须没有,否则A胜。
然后B把所有$d$都放$c$左边就可以防止最终串变成回文串并获得胜利。
WALKBT
如果是静态问题:给出一些叶子,求至少在根到一个叶子路径上的点的数目。将叶子排序后设为$a_1,a_2,\dots,a_n$,则$\sum_{i=2}^nN-LCP(a_i,a_{i-1})$就是答案。
对于动态的问题,用可持久化线段树维护所有版本的叶子,用平衡树维护叶子排序后的结果就好。在可持久化线段树上维护Hash,查LCP和比大小都是$O(\log N)$的。复杂度$O(N\log^2 N)$。
HILLJUMP
我们考虑弹飞绵羊那题的分块,这样我们只要对每个点维护它跳多少步之后跳出块,以及跳出块后跳到哪即可。另外维护一个结构支持$O(\sqrt{n})$区间加法,$O(1)$单点查询。
那么现在的问题就是维护区间加法。我们发现只有$200$个数的next需要改动($[l-100,l-1]$和$[r-99,r]$),并且(若块的大小至少是$100$)它们集中在$O(1)$个块中。为了获取新的next,我们需要提出$[l-100,l+99]$然后做一遍two pointers就可以更新$[l-100,l-1]$;提出$[r-99,r+100]$然后做一遍two pointers就可以更新$[r-99,r]$。
复杂度$O(Q\sqrt{N})$。
(感觉cc上的数据结构题都很straight forward啊??
STRINGRA
- 首先,$0,1,2,\dots,N$必须是图的一个拓扑序。
- 对任意$i$,如果$i\to i+1$的边不存在,那么无解。
-
考虑$i$和$i+1$。
-
如果$i$和$i+1$出度不同,那么说明$i+1$是某种颜色的最后一次出现,然后$i$和$i+1$的出边指向相同的地方(除去$i\to i+1$的那条);如下图
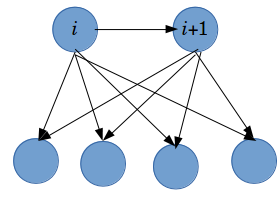
-
如果它们出度相同,那么$i$和$i+1$的出边指向相同的地方——除了$i\to i+1$的那条和某条以$i+1$为起点的$i+1\to u$。$u$和$i+1$的颜色一样。如下图
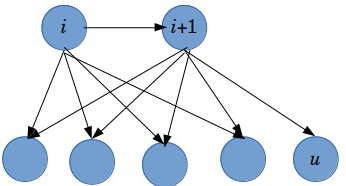
-
如果$i$和$i+1$出度不同,那么说明$i+1$是某种颜色的最后一次出现,然后$i$和$i+1$的出边指向相同的地方(除去$i\to i+1$的那条);如下图
这样可以得出(颜色个数)条链,每条链上颜色相同。字典序最小的话贪贪就好。
CHEFFA
设第$i,i+1,i+2$个位置操作$c_i$次,那么操作完之后第$i$个位置的值等于$A_i+c_{i-2}-c_{i-1}-c_i$。
实际上问的是有多少个数列$c$,使得$\forall i,A_i+c_{i-2}-c_{i-1}-c_i\ge 0$。
用$f_{i,j,k}$表示只考虑$c_{1\dots i}$,且$c_{i}=j,c_{i-1}=k$的数列的个数,dp即可。
我们可以确定$c_i$的bound:注意到操作是不改变$\sum_i\phi^iA_i$的值的,其中$\phi=\frac{1+\sqrt{5}}{2}$(因为$\phi^2=\phi+1$)。那么$c_n\le \frac{\sum_{i\le n}\phi^iA_i}{\phi^n}\le maxA\cdot\sum_{i\le n}(1/\phi)^i\le 131$。这里代入$maxA=50$。
我们还可以确定数列的长度:$\phi^{len}\le\sum_{i\le n}\phi^iA_i$,故$len\le N+\log_{\phi}(\phi+1)maxA=61$。
复杂度是$O(N^4)$的。虽然看起来常数$\phi^3$很大,但是实际上转移的条数远远不到,按照特定的方法写是可以0.02s过的。
(upd:$c_i$貌似是不超过$50$的?
FLOWERPO
有幸和rajat1603、zhouyuchen等大神同台竞技拼手速!(并且虐他们1h+
虽然这题是水题但是也比较坑了。
考虑$C=1$的情况,令$f_{i,j}$为在$j$步以内引爆$i\dots n$的最小代价,那么显然要引爆$i$,枚举$i$最多到$k$,则
$$f_{i,j}=\min_{k>i}(A_i-A_k)^2+f_{k,j-1}$$
这个dp的复杂度是$O(N^2B)$的,实际上跑得挺快的。
考虑$C\ne 1$的情况,一个想法是:令$g_{i,j}$为$j$步之内引爆$1\dots i$的最小代价,枚举$C$点的strength$s$,设影响到的点为$[i,j]$,则$g_{j,B-1}+f_{i,B-1}+s^2$为答案。
事实上这个想法(应该)是包括我在内大多数人的第一反应,但是仔细想想会发现它其实是不对的。一个反例数据是
4 3 3 1 10 13 19
正确答案是90。13引爆10,然后10干掉全场。而上面的算法会得出答案为117。上面算法错误的原因是19没有必要被13引爆。
秉持着“大胆猜想,不用求证”的爆OJ抢一血狗的精神,我们猜测答案一定是长这样的:$C$引爆另一个点$D$,然后另一个点按照刚刚的方式引爆全场。这样只要再求一个$h_{i,j}$表示$j$步从$C$引爆$i$的最少代价,然后枚举$C$用多少步引爆$D$,枚举$D$和$D$的strength,这样复杂度正好是$O(N^2B)$的。
upd:这个题居然是全场过题人数最少。。你站药丸
MATDW
瞎几把写的。。反正我排名很垃圾。。。我可能就不太适合做cha题吧。。。
 评论 (0)
评论 (0)