IBM Ponder this 2016 July

题目链接

我的题解(写得这么不清楚居然能通过)

题意就是，求一个五格骨牌的组合，其中至多包含三个五格骨牌。要求每一个$4^N\times 4^N$的棋盘去掉任意一个格子之后都可以被这个组合拼出来。骨牌可以旋转和翻转。

例如：考虑r型三格骨牌，它可以拼出任意$2^N\times 2^N$的棋盘去掉任意一个格子。

我开始不知道能否翻转。。给出了一个$2$个块(可以翻转)，$3$个块(不能翻转)的方案。。自我感觉还不错吧。。

现在开始剧透

答案是

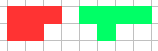
(答案不唯一)

证明：首先考虑用这两个小家伙拼出大一倍的家伙：

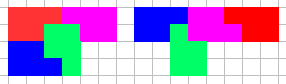
这样，通过一次一次地迭代可以构造出边长是原图像的$2^k$倍的块，其中$k$是任意自然数。

然后考虑用它们拼出$4\times 4$的情况：

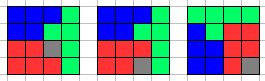
注意因为允许旋转和翻转，所以只要考虑这三种情况。

现在考虑$4^N\times 4^N$的情况，把棋盘分成$4\times 4=16$个块，每个块的大小是$4^{N-1}\times 4^{N-1}$。恰有一个块包含被删掉的空格，对这个块递归，考虑覆盖剩下的块，其实这就是拿大小为$2^{N-1}$倍的东西覆盖$4\times 4$的棋盘，显然可做。

发现这玩意很难表述清楚。。就算是用中文啊