codechef JAN17

在微积分和抽代的紧逼之下打开了这个熟悉的网站作死

只有4个题按时出炉了。。垃圾比赛

ps.最终TUPLES没有调出来。。嘴巴了一下。。还有一个傻逼题没做。。。

CHEFCIRC

mgch的原题大赛?原题也是$n\le 500$。。做着这个题我仿佛又回到了2.5年前悟出这个算法的时光。。

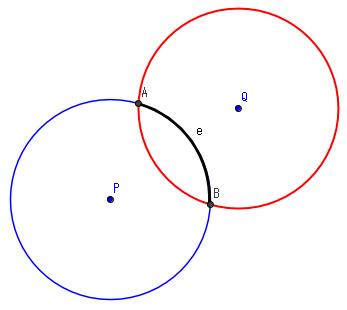
枚举一个点$P$，假设这个点一定被选。二分答案$r$，圆心(设为$O$)一定在以$P$为圆心，$r$为半径的圆(即蓝圆)内。如果还要选点$Q$，那么$O$一定在以$Q$为圆心，$r$为半径的圆(红圆)内。也就是说，如果$P$被选，那么要保证$Q$被选则$O$一定要在红蓝两圆之交中。$P$到$O$的连线与蓝圆有一个交点，这个交点一定在弧$AB$上。对每个不等于$P$的点，我们求出它对应的弧然后做区间覆盖。对一个点和一个$r$的复杂度是$O(n\log n)$的。

换言之，对一个$P$和一个$r$我们可以$O(n\log n)$地求出覆盖$P$的半径为$r$的覆盖了$M$个点的圆是否存在。枚举$P$并二分答案就可以得到$O(n^2\log n\log r)$的算法了。

我们把点随机打乱，并维护当前求得的$r$的最小值$ans$。考虑按照随机的顺序访问这些点，访问一个点$P$的时候，看覆盖$P$的半径为$ans$的圆可不可以覆盖$M$个点(这一步称为“检验”)，不可以的话就把$P$忽略；否则继续二分答案，因为此时$ans$肯定能被更新，所以我们把这一步称为“更新”。

我们分析一下时间复杂度：检验的复杂度是$O(n^2\log n)$。第$i$个点会进入“更新”的充要条件是它的答案优于它前面所有点的答案，概率为$\frac{1}{i}$，所以更新的复杂度为$O((n\log r)(\sum_{i=1}^n\frac{1}{i}))=O(n\log n\log r)$。总时间复杂度$O((n+\log r)n\log n)$。

CATSDOGS

首先，$L$一定是$4$的倍数；$L/4$即为站立的动物的数量$S$。$c=S-H$即为站着的猫的数量，这个数必须$\ge 0$；$C-c$即为骑♂着狗的猫的数量，这个数必须在$[0,\min(C,2H)]$之间。满足这些条件就yes，否则就no。

CAPIMOVE

感觉这个英文题面语死早?就是问把$V$和其邻点删掉之后权值最大的点编号是谁，对每个$V$输出答案。

设$c$为原首都，显然只需要考虑与$c$距离不超过$1$的点。我们以$c$为根，求一遍子树max各种搞搞就好了。

讲道理这题我写萎了至少5处还写了拍。。耻辱

TUPLES

令$M=359999$。这题分为两部分。

1.求$X_iX_j\equiv s\pmod M$的方案数$f_s$。注意到$M=599\times 601$为两个质数的乘积。令$c_{i,j}$为模$599$为$i$，模$601$为$j$的数的个数，即求$f_{a,b}=\sum_{ik=a,jl=b}c_{i,j}c_{k,l}$。

若$a,b$均不为$0$，我们把每个数用原根代替做fft即可。具体地说，令$g_1,g_2$为模$599,601$的原根($g_1=g_2=7$)，$c'_{i,j}=c_{g_1^i,g_2^j}$，$f'_{i,j}=f_{g_1^i,g_2^j}$，则$f'_{a,b}=\sum_{i+k=a,j+l=b}c'_{i,j}c'_{k,l}$。这就是一个普通的二维卷积，做fft就好。

若$a=0,b\ne 0$，我们需要求$f_{0,b}=2\sum_{jl=b} c_{0,j}c_{k,l}-\sum_{jl=b} c_{0,j}c_{0,l}$。若干次长为$601$的卷积。

若$a\ne 0,b=0$：同上

剩下的就是$a=0,b=0$的情况了。

2.求$\sum_{(i,j,k)=1}f_if_jf_k$。如果$f_0=0$的话，瞎jb反演就可以了。

\begin{eqnarray*}
&&\sum_{(i,j,k)=1}f_if_jf_k\\
&=&\sum_{t}\mu(t)\sum_{i,j,k}f_{it}f_{jt}f_{kt}\\
&=&\sum_{t}\mu(t)F(t)^3
\end{eqnarray*}

其中$F(t)=\sum_{t\mid k}f_k$可以$O(M\log M)$求，求出$F(t)$之后上面那个柿子可以$O(M)$求。

在有$f_0$的情况，我们要分取了几个$0$讨论，最终的柿子大概是$\sum_t\mu(t)((F(t)+f_0)^3-f_0^3)$吧。

FOURSQ

根据拉格朗日四平方和定理，每个正整数都可以表示为四个平方数之和。证明如下：根据Fermat's two-square theorem，任意形如$4p+1$的素数都可以表示为$a^2+b^2$；那么任意形如$4p+3$的素数都可以表示为$a^2+b^2+1^2+1^2$；再特判一下$2$就知道任意素数都是四个平方数之和。又因为(Euler's four-square identity)，我们知道$a,b$可以表示为四个平方数之和则$ab$也可以。故拉格朗日四平方和定理得证。

用到这个题上来：因为根据$a,b$的四平方和表示法可以得到$ab$的四平方和表示法，询问的那个数又是若干个不超过$10^6$的数之积，所以我们只需要将$1\dots 10^6$表示为四平方和即可，然后再线段树xjb搞搞就作完了。

怎么将$1\dots 10^6$内的所有数都表示成四平方和呢?首先我们可以用$10^6$的复杂度将可以表示为两平方和的数给选出来，然后对每个不能被表示为两平方和的数$i$，我们暴力寻找最小的$j$使得$j,i-j$都可以表示为两平方和。这个实际上跑得飞快。

复杂度$O(10^6+TQ\log N)$。

TOURISTS

输入一张无向图，把边定向使得图有经过每个点的欧拉回路。

图必须连通；每个点度数必须是偶数。

如何构造解呢，考虑令$d_i$为$i$的入度减出度，我们每次选择两个$(i,j)$，使得$i$有到$j$的路径，$d_i<0$，$d_j>0$，然后把$i$到$j$的某条路径上的边反向。可以看到这样子只会影响$i,j$的$d$值，且$d_i+=2,d_j-=2$。只要存在这样的$(i,j)$我们就继续执行这个操作。如果图的答案是YES，且存在$d_i<0$的点$i$(那么当然存在$d_j>0$的点$j$)，那么一定存在满足上述条件的$(i,j)$。不然，你考虑$i$能到的所有点的导出子图，会发现这个图的总入度小于总出度，矛盾。

我们发现。。这就是在模拟网络流的过程：每次找到一条增广路，并把它增广。我们新建两个点$S,T$，$S$向每个$d_i<0$的点连容量为$-\frac{d_i}{2}$的边，$d_i>0$的点向$T$连容量为$\frac{d_i}{2}$的边，原来的图中边权都是$1$，然后找一个比较快的网络流算法跑一遍就好了。有流经过的边就是需要改方向的。

亲测0.04s虐爆所有数据。

(upd.好像。。这题就是。。找欧拉回路?所以经典算法$O(N+M)$就可以过了?)

DIGITSEP

我会做bonus。。转成ascii码之后发现是?v=.....，所以打开youtube.com/watch?v=...就可以看到"hiddle treasure"了，不过没什么卵用。

这个题的话。。好像又是个语死早的题目。。大意就是把数字串分成$p(x+1\le p\le y+1)$段，使得每一段长度不超过$m$，最大化所有段的gcd

有可能成为答案的数一定是某个长度不超过$m$的子段的因数。$n=1\to 10$时，不超过$10^{n}$的反素数的因子数为$\{4,12,32,64,128,240,448,768,1344,2304\}$(见这里)，故可能出现的数有$5344\times 300=1603200$个(其实应该小很多。。几千几万就算多的了)。

对每一个可能出现的数$G$，我们令$f_{i,j}$表示$1\dots i$分成$j$段，每一段长度都不超过$m$且都是$G$的倍数，是否可能。这个dp可以压位跑一跑。复杂度我不会算。。

然后这样会被卡。我用一些肮脏的手段卡过去了。。比如说，把一个$G$的所有可能的转移事先存下来，而不是$O(nm)$无脑跑转移；如果转移的个数太少($<n/m$)，那么可以丢掉这个$G$(这是个很叼的优化)。于是成功贴线低飞辣。

SEABOX

考虑令$f_{B,x}$表示Box $B$修改$x$个数可以达到的最小$F$值。那么数组$F_B$可以由$F_{B_1},\dots,F_{B_8}$转移过来，其中$B_1\dots B_8$就是$B$被分成的$8$块。这是个背包问题，复杂度$O(|B|^2)$。最大$F$值同理。

设$N=2^Q$，总复杂度$\sum_{i=1}^Q8^{Q-i}8^{2i}=8^{2Q}$，即复杂度$O(N^6)$。我们发现这个题是sereja出的，所以这个复杂度应该可以过了。

暴力写当然过不了咯，但是如果卡卡背包size上界的话就随便过了咯。比如说求最大$F$值的时候，显然至多改$\frac{N^3}{8}$个量，其中包含着一个很小的常数。