一个简单题和一个不简单的证明

求证：$n$个点$n+4$条边的无向简单图中一定存在两个边不相交的环。

这是计应数习题课的一个题目。lljz大佬给出了一个非常漂亮的证明。(不过我并不知道有没有更漂亮的证明)

先写一下经典的证明吧。

首先我们注意到度数为$1$的点是可以去掉的。

然后我们注意到度数为$2$的点是可以缩掉的。就是，$v$只与$u_1,u_2$相连，那么删掉$v$，给$u_1,u_2$加一条边。

这里有个小细节。如果$u_1,u_2$之间本来就有边，那么图就不是简单图了。然而我们可以假定所有环的长度$>4$，因为否则的话把这个环删掉之后图中显然还有环。这样上面$u_1,u_2$的情况就不会发生了。

最后，每个点的度数$\ge 3$，所以边数$\ge \frac{3}{2}n$。这样$n+4\ge \frac{3}{2}n$，解出$n\le 8$。

然后暴力枚举所有$n\le 8$的图，发现结论都成立。证毕。

我的感觉是。。这个证明最后那一步暴枚太不优美了。。但是我问助教有没有什么办法避免暴枚，好像是没有的。

下面是lljz的证明。lljz是个脑洞非常大的神犇。。

如果这个图是平面图，那么根据欧拉公式，它有$6$个面，根据四色定理(五色就可以了?)，可以把所有的面四染色，这样存在两个面颜色相同，这两个面满足边不相交。

否则，如果这个图有$K_5$的subdivision，那么$v_1-v_2-v_3$和$v_1-v_4-v_5$即可。

最后的，也是最棘手的情况——这个图有$K_{3,3}$的subdivision。反证法，假设图不存在边不相交的两个环。

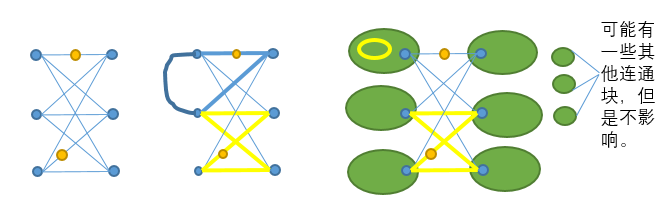
如左图，将蓝色的$9$条链以及链上的所有黄点(这个图是$K_{3,3}$的subdivision，边上可能有点)全都删掉。如果有两个蓝点仍然连通，那么中间那张图中的两个环(蓝色和黄色的粗线)满足边不相交；这样的话，每个蓝点属于一个连通块。右图用绿色椭圆表示连通块。如果某个连通块内部有环，如右图，我们就找到了两个环(右图中的黄色环)满足边不相交。所以连通块都无环，故边数最多比点数多$3$，矛盾。

hhh这是不是四(五?)色定理的一个意想不到的应用。。反正我看到这种脑洞大开的证明时还挺惊讶的。