CCC 2021 游记
人生中第二次参加CCC!仍然是在这个博客上记录一些自己喜欢的paper(其实是听talk的时候听懂了的paper)。很多paper我都不熟悉所以我就只把结论摘抄一下(而不做点评了)。
有几篇证明复杂度(proof complexity)的talk没有听懂呜呜呜
Quantum Complexity of Minimum Cut
本文研究的是求最小割的量子复杂度。给出一张无向无权图,每次可以询问邻接矩阵某个矩阵中的某个元素,请问至少需要多少次询问可以求出这张图的最小割?在询问复杂度(query complexity)的计算模型中,我们只考虑询问的次数而不考虑其他计算的复杂度。
如果只允许经典询问的话,可以证明$\tilde{\Omega}(n^2)$次询问是必须的。如果允许量子询问的话,前人的工作证明了就算是判断连通性也至少需要$\tilde{\Omega}(n^{3/2})$次询问。本文的主要结果是一个$\tilde{O}(n^{3/2})$次询问求出最小割的算法。其主要用到的技术如下:
-
首先,本文使用了Kawarabayashi-Thorup的如下结论:只有$O(n)$条边可以在“几乎”最小的割中出现。具体地说,我们总是可以把图的点集划分为若干块,使得(1) 所有“几乎最小”(大小不超过$1.1$倍最小割)且“非平凡”(两边都有至少两个点)的割都不会割开这些块(而是完整地保留每一块);(2) 块间的边数只有$O(n)$。
- 其次,本文使用了Apers-de Wolf的量子图稀释算法。一张图$G$的一个cut sparsifier是指$G$的一个子图$H$($H$中的边的权值可能和$G$中不一样),使得(1) $H$是稀疏的(也就是顶多有$O(n)$条边);(2) $H$中的割和$G$中的割大小差不多(对每个割集$(S, V-S)$,它在$G$中和在$H$中的割的大小顶多差$(1\pm \epsilon)$倍)。Apers-de Wolf给出了一个用$\tilde{O}(n^{3/2})$次量子询问构造一个cut sparsifier的算法。
有了这些技术之后,我们就可以在$\tilde{O}(n^{3/2})$次量子询问内求出最小割了:
- 首先利用Apers-de Wolf求出一个cut sparsifier $H$(使用$\tilde{O}(n^{3/2})$次询问)。
- 接下来构造出$H$的Kawarayabashi-Thorup划分(这部分不需要询问,所以可以认为是免费的)。
- 求出K-T划分中所有块间的边。由于只有$O(n)$条边,这部分使用Grover搜索可以做到$\tilde{O}(n^{3/2})$次询问。
- 按照K-T划分将原图缩起来并把第3步找到的块间边加进去。在这个新的图上求最小割,一定就是原图的最小割。
这样可以做到$\tilde{O}(n^{3/2})$次量子询问。事实上,本文还给出了第2步的$\tilde{O}(n^{3/2})$时间的量子算法,所以上述算法也可以做到$\tilde{O}(n^{3/2})$的量子时间复杂度。
(注:本文中也有针对带权图和邻接表模型的结果,但是这里我懒得写了。)
Fourier Growth of Parity Decision Trees
emmm其实我没有很仔细地关注这篇文章的细节。。。但是我打算摘抄里面的一个引理——“自适应Azuma不等式”(adaptive Azuma's inequality)。(因为以后也许会用上。。。)
Azuma不等式是指如下的定理:设$X_0 = 0$且$X_i = X_{i-1} + \delta_i \cdot r_i$,其中$r_i$是独立随机变量,满足$|r_i| \le 1$且$\mathbb{E}[r_i] = 0$;且$\delta_i$是只和$r_1, r_2, \dots, r_{i-1}$相关的量(也就是与$r_i$无关)。那么,如果$|\delta_i| \le c_i$,则
\[\Pr[|X_n| \ge t\sqrt{\sum_i c_i^2}] \le 2e^{-2t^2}.\]
然而这篇文章在分析parity decision tree时,好像并没有统一的$|\delta_i|$的上界?于是这篇文章需要一个“自适应”的Azuma不等式:设$X_i, \delta_i, r_i$的定义和上述红字部分一样。如果以$1-\epsilon$的概率,$\delta_i$满足$\sum_{i=1}^n|\delta_i|^2 \le U$,那么
\[\Pr[|X_n| \ge t\sqrt{U}] \le 2e^{-2t^2} + \epsilon.\]
(注:代入$U = \sum_i c_i^2$,可以验证标准的Azuma不等式的确是上述定理的特例。)
A Majority Lemma for Randomised Query Complexity
本文研究的是复合函数的询问复杂度。设$f:\{0, 1\}^n \to \{0, 1\}$和$g:\{0, 1\}^m\to\{0, 1\}$为两个函数,那么$f\circ g^n$是如下$\{0, 1\}^{nm}\to\{0, 1\}$的函数:
\[(f\circ g^n)(x_1, x_2, \dots, x_n) = f(g(x_1), g(x_2), \dots, g(x_n)).\]
可以证明,如果$f$和$g$的确定性询问复杂度分别是${\rm D}(f)$和${\rm D}(g)$,则$f\circ g^n$的询问复杂度恰好是${\rm D}(f)\cdot {\rm D}(g)$。那么对于随机复杂度呢?令${\rm R}_{\epsilon}(f)$为允许以$\epsilon$概率出错的随机复杂度,${\rm R}(f) = {\rm R}_{1/3}(f)$。一个显然的上界为:${\rm R}(f\circ g^n) = O({\rm R}(f)\cdot {\rm R}_{1/n}(g))$。注意这个下标$1/n$:我们想利用一个解决$g$的随机算法$n$次,于是我们需要这个算法的错误率顶多是$1/n$(这样才能用union bound)。
(注:简单起见,这里不区分最坏意义的随机复杂度${\rm R}$和期望意义的随机复杂度$\overline{\rm R}$。见论文的第一页。)
对于某些$f$,这个$1/n$的下标并不是必要的:例如当$f = {\sf OR}_n$时,${\rm R}(f\circ g^n) = O({\rm R}(f)\cdot {\rm R}(g))$。然而,对于另一些$f$,这个$1/n$的下标就是必要的了:例如当$f = {\sf XOR}_n$时,${\rm R}(f\circ g^n) = \Omega({\rm R}(f)\cdot {\rm R}_{1/n}(g))$。这篇文章的结果是:当$f = {\sf MAJ}_n$时,这个$1/n$的下标是必要的。
事实上,这篇文章证明了对任意$f$,如果当$g={\sf GapOR}_{\log n}$的时候一个足够强的结论成立(“$\deg_{\epsilon}^+(f\circ g^n)\ge \Omega(n\log n)$”),那么上述的$1/n$下标就是必要的。前人的工作证明了该结论对${\sf MAJ}$成立,于是这篇文章对${\sf MAJ}$的结果也就成立了。
A Lower Bound on Determinantal Complexity
我觉得题目挺有意思,所以就抄一下这篇文章的结果。一个多项式$f$的行列式复杂度(determinantal complexity)是指最小的数$m$,使得存在一个$m\times m$的矩阵$M$,其中每个元素都是一个仿射变换($1, x_1, x_2, \dots, x_n$的线性组合),且$\det(M) = f$。如果一个多项式有大小为$s$的代数公式(algebraic formula)那么其行列式复杂度也至多是$s$。${\sf VP} = {\sf VNP}$当且仅当积和式的行列式复杂度是${\rm poly}(n)$。
行列式复杂度下界一直没有什么进展。事实上,直到这篇文章才证出了第一个$>(1+\Omega(1))n$的行列式复杂度下界:这篇文章证明了多项式$\sum_{i=1}^nx_i^n$的行列式复杂度至少是$1.5n - 3$。(看上去比电路复杂度还惨啊,笑)
Hardness of KT Characterizes Parallel Cryptography
这是我参与的paper!我们当时读了Liu-Pass的工作之后受益匪浅,于是搞了这么个东西出来。Liu-Pass证明了单向函数存在当且仅当${\rm K}^{\rm poly}$在平均复杂度意义下是困难的。我们想:为什么偏偏是${\rm K}^{\rm poly}$而不是${\sf MCSP}$呢?于是我们玩了玩${\sf MCSP}$和它的近亲${\sf MKTP}$,并且有了这篇paper。
我们证明了如下结论:${\rm KT}$在平均复杂度意义下是困难的当且仅当存在${\sf NC}^0$中的单向函数!(我相信如果你读懂了Liu-Pass的话这个结论其实还蛮显然的,手动狗头。)令我本人比较惊讶的是,${\rm KT}$也能恰好对上某个密码学问题,但这个问题并不是“单向函数的存在性”——而是“${\sf NC}^0$中单向函数的存在性”。
对了,“${\sf NC}^0$中的单向函数”是一个之前就有很多人研究的问题。Applebaum-Ishai-Kushilevitz证明了任何一个${\sf NC}^1$中的单向函数(或者甚至$\oplus{\sf L}$中的单向函数)都可以被转化为${\sf NC}^0$中的单向函数——这给${\sf NC}^0$中的单向函数的存在性提供了非常有力的证据(虽然${\sf NC}^0$是一个很弱的复杂度类)。我们证明了这类单向函数的存在性可以由${\rm KT}$的平均复杂度来刻画!我:靠AIK吃饭的三流研究员wwww
以及我很想推销我们的另一个结果:我们给出了由${\sf NC}^1\text{-}{\rm K}^{\rm poly}$到${\rm KT}$的平均复杂度规约。这个结果是受到了前一个结果的启发,用的也是AIK的技术,所以我们放到了同一篇paper里面。由于不同的Kolmogorov复杂度之间一般来说是没有什么规约的,所以这个结果令我挺惊讶的。有兴趣的同学可以去读读我们的paper。
On the Pseudo-deterministic Query Complexity of NP Search Problems
这也是一篇询问复杂度的文章。这篇文章关注的是如下的问题(“FIND1”):给出一个长度为$n$的串$x$,保证$x$中至少有$n/2$个$1$,要求找到一个$i$使得$x_i = 1$。请问至少需要多少次询问?
- 对于确定性算法,很容易证明至少需要$\Omega(n)$次询问。
- 对于随机性算法,我们只要不断地随机找$i$直到找到为止,只需要$O(\log(1/\epsilon))$次询问就能够保证$1-\epsilon$的成功概率。
那么如果我们考虑伪确定性(pseudo-deterministic)算法呢?一个伪确定性算法可以使用随机数,但是要求它长得像一个确定性算法:对每个输入$x$,都存在一个特定的合法解$i_\star$,使得这个算法以$1-\epsilon$的概率恰好输出$i_\star$。naive的随机算法不是伪确定性的,因为当随机数不同的时候,它输出的答案$i$很大概率也是不同的。
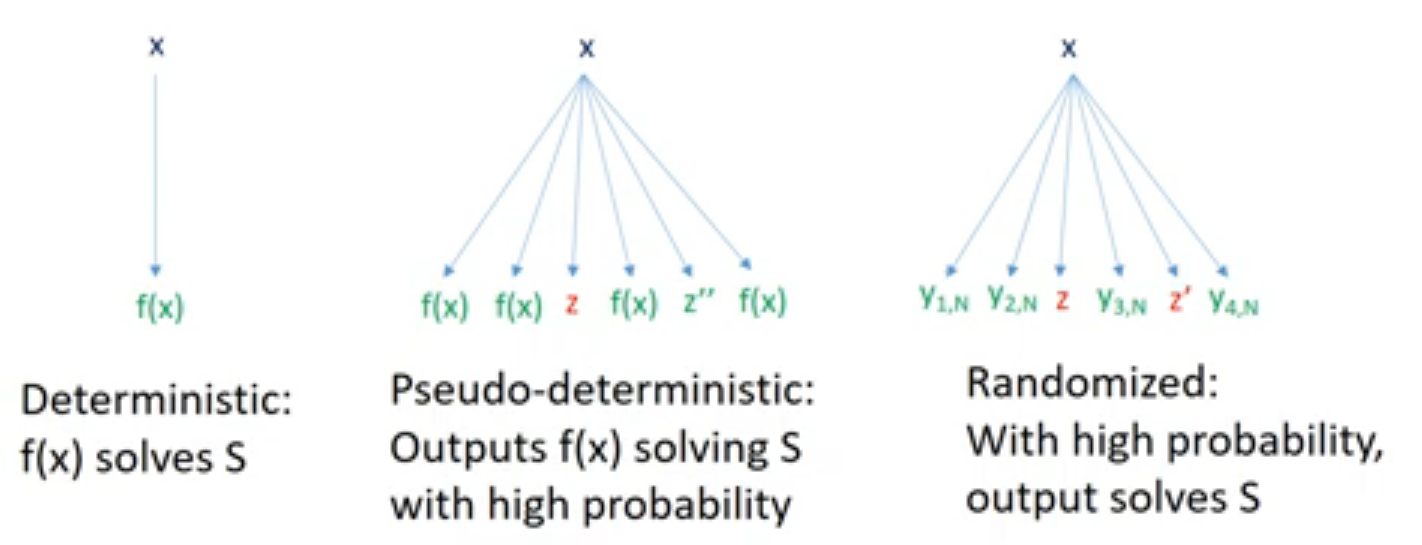
这篇文章的主要结果是:任何一个解决FIND1问题的伪确定性算法需要$\Omega(\sqrt{n})$次询问。这个下界对量子算法也成立,所以它是紧的(Grover搜索可以做到$O(\sqrt{n})$)。对于经典算法我们不知道它是不是紧的。同时,这个结果也能够推出一些证明复杂度的下界(关于Pseudo-deterministic Tree Resolution的,我没仔细看)。
Arithmetic Circuit Complexity of Division and Truncation
先讲division。代数电路是只允许使用加法($+$)和乘法($\times$)门的,而不允许使用除法($\div$)门。于是我们可以研究如下的问题:假设两个多项式$g$和$h$都有较小的代数电路,且$g/h$也是一个多项式,那么是否意味着$g/h$也有一个较小的代数电路呢?本文证明了如果$h$的度数较小的话,那么问题的答案是肯定的:如果$g,h$的代数复杂度均不超过$s$,那么$g/h$的代数复杂度不超过$O(s\cdot \deg(h)^2)$。
视频里也讲了这个结论的证明,不过我没太看懂一般情况,我只看懂了单变量多项式的特殊情况。假设$g(x)$有大小不超过$s$的代数电路$C_g$。我们把$C_g$中的每个门$u$都换成两个门$u_{\sf div}\,$和$u_{\sf mod}$。其中$u_{\sf div}\,$计算$u~{\rm div}~h$的值,$u_{\sf mod}\,$计算$u\bmod h$的值。
-
如果$u=v+w$,那么
\begin{align*}
u_{\sf div}=&\,v_{\sf div}+w_{\sf div}\\
u_{\sf mod}=&\,v_{\sf mod} +w_{\sf mod}
\end{align*} -
如果$u = v\times w$,那么
\begin{align*}
u_{\sf div} =&\, v_{\sf div}\times w_{\sf div}\times h + v_{\sf div}\times w_{\sf mod} + v_{\sf mod}\times w_{\sf div} + (v_{\sf mod}\times w_{\sf mod}~~{\rm div}~h)\\
u_{\sf mod} =&\, (v_{\sf mod}\times w_{\sf mod}~\bmod h)
\end{align*}
于是我们只需要计算$v_{\sf mod}\times w_{\sf mod}~~{\rm div}~ h$和$v_{\sf mod}\times w_{\sf mod}~\bmod h$即可,可以用$O(\deg(h)^2)$个门计算出来。
再讲truncation。给出一个形式幂级数$f(x) = \sum_{i\ge 0}a_ix^i$,问$f(x)\bmod x^d$是否有大小为${\rm poly}(\log d)$的代数电路?如果答案为“是”,那么我们说这个形式幂级数是简单的,否则是困难的。这篇文章证明了:如果我们只允许代数电路使用常数$-1,0,1$(而不能使用绝对值更大的常数),并假设分解质因数需要的电路大小是超多项式的,那么$f(x) = \sqrt{1 + 4x}$是困难的。
 评论 (0)
评论 (0)