费马平方和定理的一句话证明

今天（Nov 22, 2021），Christ Church Math & CS 社区组织了一次活动，每个大三的学生要上台做一个演讲。我觉得比较有意思就去旁听了。我个人最大的收获是一个关于费马平方和定理的演讲。该定理是这样的：

定理：设$p$为奇质数。则$p$能被写成两个整数的平方和（即$p=a^2 + b^2$）的充要条件是$p\equiv 1 \pmod 4$。

注意，如果$p\not\equiv 1\pmod 4$，那么$p\equiv 3\pmod 4$，而此时$p$显然是不能写成两个整数的平方和的。也就是说，我们很容易证明$p\equiv 1\pmod 4$是必要条件。所以我们接下来只考虑另一个方向，也就是证明$p\equiv 1\pmod 4$是充分条件。

这个定理有一个惊为天人的一句话证明：

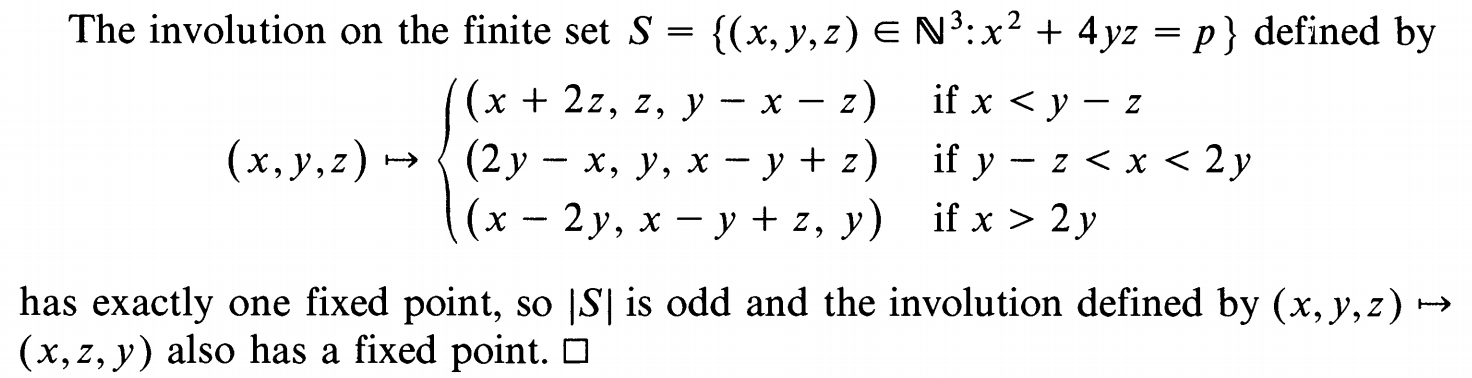让我解释一下这个证明。我们首先构造一个集合

\[S = \{(x, y, z) \in \mathbb{N}^3 : x^2 + 4yz = p\}\]

如果$S$的大小是奇数，那么$p$可以被写成$a^2 + b^2$的形式。这是因为对任意$(x, y, z) \in S$，$(x, z, y)$显然也在$S$中。如果对任意$(x, y, z)\in S$有$y\ne z$，那么我们可以把每个$(x, y, z)$和$(x, z, y)$配对，于是$S$的大小一定是偶数。而此时$S$的大小是奇数，所以一定存在$(x, y, z)\in S$使得$y = z$。这个时候我们就有

\[p = x^2 + (2y)^2.\]

于是，我们的目标就变成了证明$S$的大小是奇数。我们刚刚构造了一个$S$上的对合，这个对合把$(x, y, z)$映到$(x, z, y)$。（注：对合 / involution 指一个函数$f:S\to S$使得对任意$x$，$f(f(x)) = x$。）我们现在要构造另一个$S$上的对合$g$，使得$g$有恰好一个不动点。由于$g$有恰好一个不动点且$g(g(x))$总是等于$x$，我们就可以把所有的$x$和$g(x)$配对。除去这唯一一个不动点以外每个点都和另一个点配对了，所以$S$的大小是奇数。

现在我们构造$g$：

\[
g(x, y, z) = \begin{cases}
(x+2z, z, y-x-z) & \text{if }x < y - z\\
(2y-x, y, x-y+z) & \text{if }y-z < x < 2y\\
(x-2y, x-y+z, y) & \text{if }x > 2y\\
\end{cases}
\]

首先，可以验证$g(x, y, z)$总是$S$中的元素：

\begin{align*}
(x+2z)^2 + 4z(y-x-z) =&\,x^2 + 4yz;\\
(2y-x)^2 + 4y(x-y+z) =&\,x^2 + 4yz;\\
(x-2y)^2 + 4y(x-y+z) =&\,x^2 + 4yz.
\end{align*}

把$(x, y, z)$满足$x < y - z$称作“情况1”，满足$y - z < x < 2y$称作“情况2”，满足$x > 2y$称作“情况3”。那么可以看到$g$把“情况1”映到“情况3”、把“情况2”映到“情况2”、把“情况3”映到“情况1”。于是

\begin{align*}
(x, y, z) &\,\mapsto^g (x+2z, z, y-x-z) \\
&\,\,\mapsto^g ((x+2z) - 2z, (x+2z) - z + (y-x-z), z) = (x, y, z) & \text{if }x < y-z\\
(x, y, z) &\,\mapsto^g (2y-x, y, x-y+z) \\
&\,\,\mapsto^g (2y-(2y-x), y, (2y-x)-y+(x-y+z)) = (x, y, z) & \text{if }y-z < x < 2y\\
(x, y, z) &\,\mapsto^g (x-2y, x-y+z, y) \\
&\,\,\mapsto^g ((x-2y)+2y, y, (x-y+z)-(x-2y)+y) = (x, y, z) & \text{if }2y < x\\
\end{align*}

于是我们验证了$g$的确是个对合。

最后，$g$的不动点只能在“情况2”中找。设这个不动点为$(x, y, z)$，则$x=2y-x$且$z=x-y+z$，也就是$x=y$。那么$x(x+4z) = p$。由于$p$是质数且$p\equiv 1\pmod 4$，一定有$x=1$且$z = (p-1) / 4$。换句话说，$(1, 1, (p-1)/4)$是$g$的唯一的不动点。

于是，我们构造了一个$S$上的对合$g$，且$g$有唯一的不动点。这意味着$S$的大小是奇数。根据前面的论证，存在$(x, y, z)\in S$使得$y = z$，此时$p = x^2 + (2y)^2$。证毕。

看完这个证明之后，很自然地会冒出这样一个想法：这个对合$g$是如何构造出来的？背后有没有什么直觉？原论文说$g$的构造是从一个拓扑学版本的证明中提炼出来的，但是这个说法貌似并不能让人理解$g$背后的意义。

幸运的是，我听的那个演讲中给出了一个漂亮的解释！这个$g$的构造并不是空穴来风的，它背后的几何意义如下。（后来我在 MathOverflow 上也找到了相关的回答。还有一个视频。）

我们定义一个风车型为：一个正方形按照如图所示在四个角上挖掉四个全等长方形所组成的图形。

一个风车型显然可以拆成一个正方形加上四个全等长方形的形式。设正方形的边长为$x$，长方形的大小为$y\times z$，那么风车型的面积就是$x^2 + 4yz$。

事实上，一个相同的风车型有两种拆法！如下图所示。

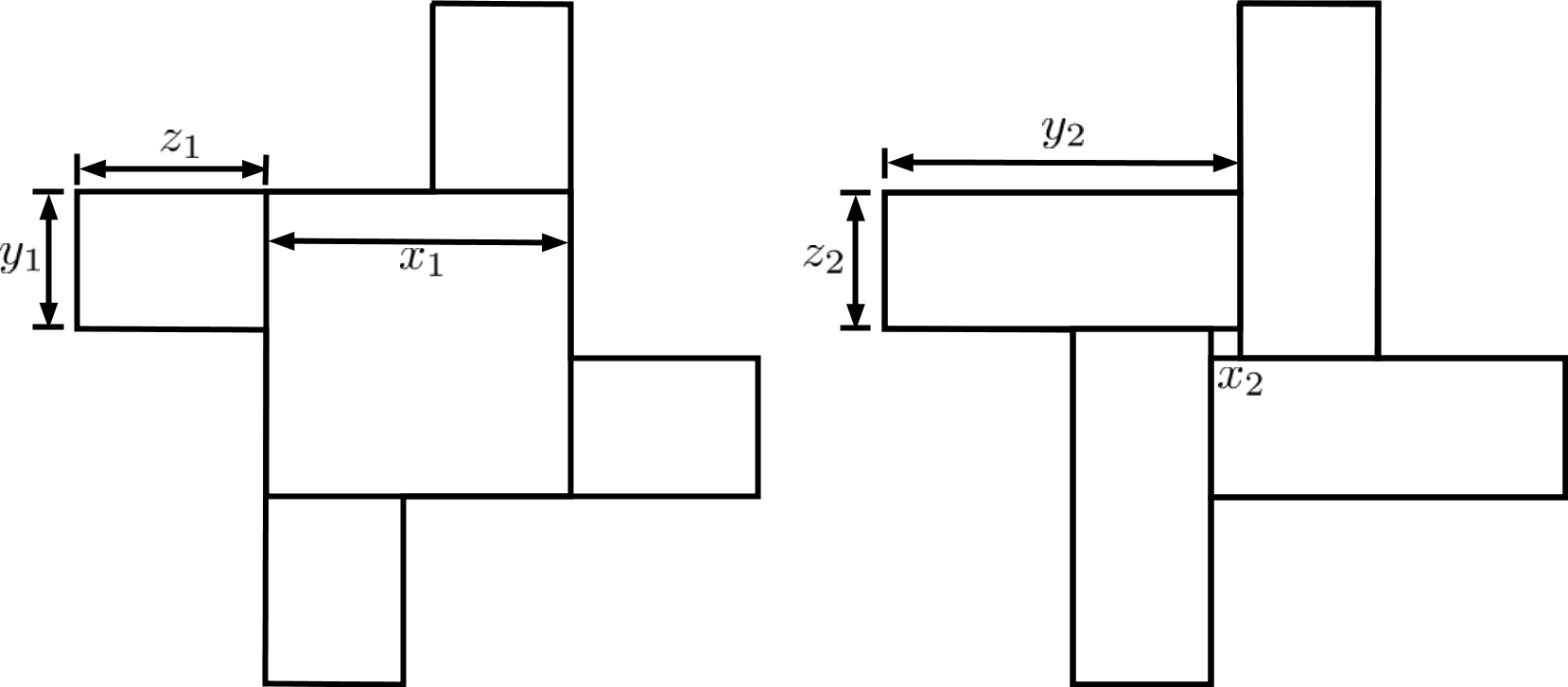
上图左显示的是$x_1 > 2y_1$的情况（“情况3”），上图右显示的是$x_2 < y_2 - z_2$的情况（“情况1”）。可以验证

\begin{align*}
x_2 =&\, x_1-2y_1;\\
y_2 =&\, x_1-y_1+z_1;\\
z_2 =&\, y_1.
\end{align*}

也就是说

\[(x_2, y_2, z_2) = g(x_1, y_1, z_1).\]

（同理也可以验证$(x_1, y_1, z_1) = g(x_2, y_2, z_2)$。）

我们同样可以考虑$y_1 - z_1 < x < 2y_1$的情况（“情况2”）：

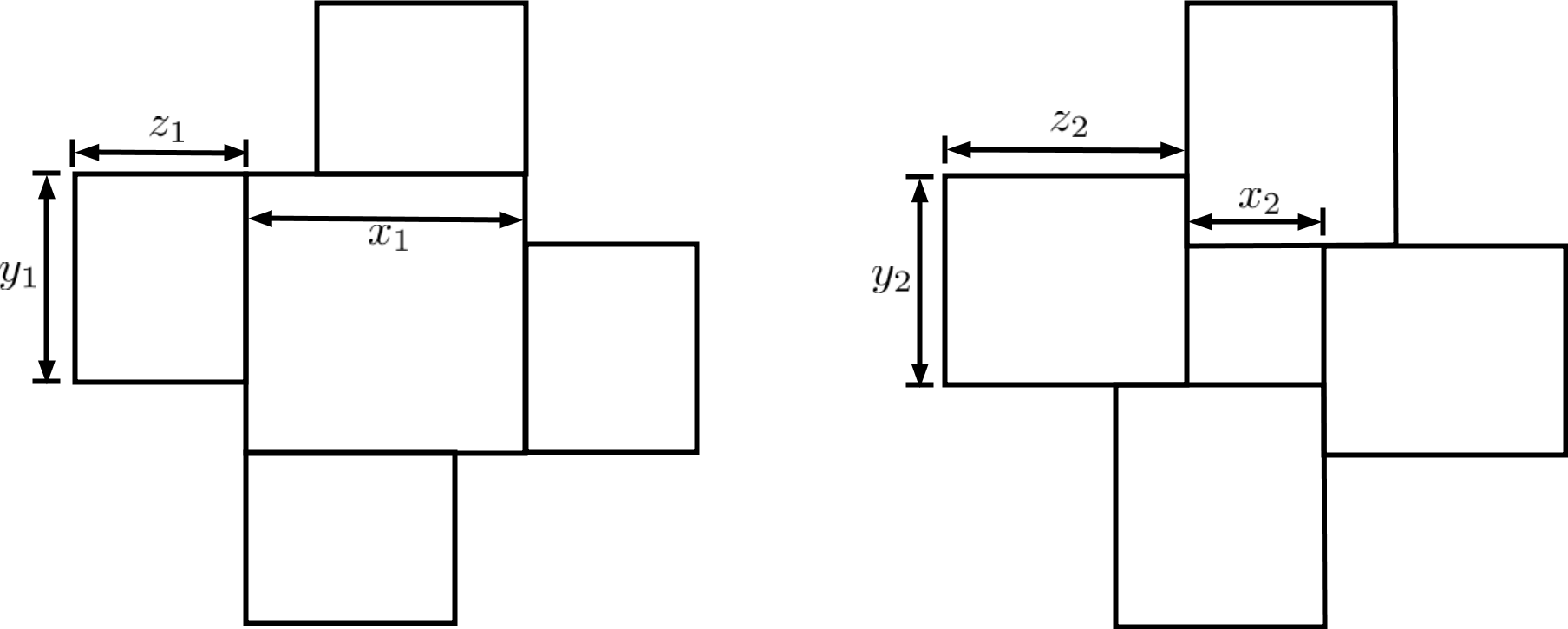
可以验证

\begin{align*}
x_2 =&\, 2y_1-x_1;\\
y_2 =&\, y_1;\\
z_2 =&\, x_1-y_1+z_1.
\end{align*}

也就是

\[(x_2, y_2, z_2) = g(x_1, y_1, z_1).\]

于是，$g$的定义就很清晰了：$g(x, y, z)$就等于$x^2+4yz$所定义的风车型的另一种拆法！当我们严格地写出“风车型的另一种拆法”的表达式时，会发现需要按照$g$的定义式中分三种情况讨论。于是$g$就会有这么一个看上去很复杂的定义——但是它本质上说的就是“风车型的另一种拆法”。

所有的风车型都有两种拆法，但是有一个例外：十字型。（也就是说$y = x$的情况，如下图。）

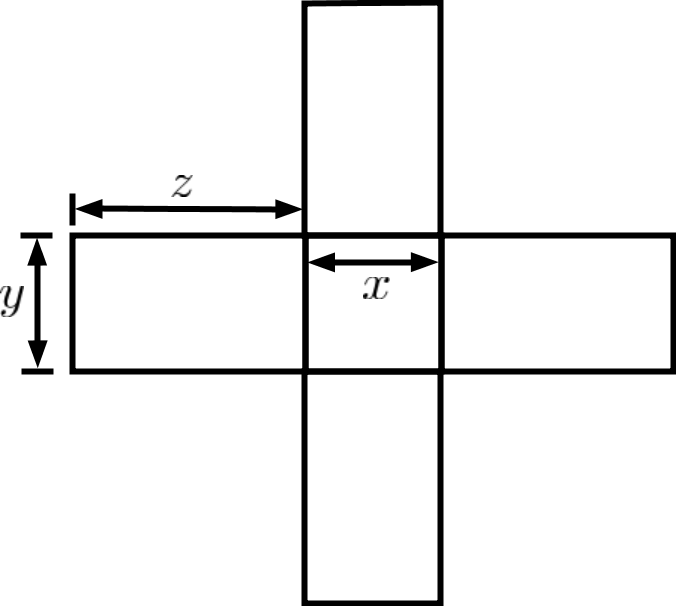
现在，我们用“风车型”的语言来复述一遍上面的一句话证明。令$p$为一个模$4$余$1$的质数。回忆一下：只要证明$|S|$是奇数，就能证出$p$能够表示成两个平方数之和。

我们考虑所有（边长为整数且）面积为$p$的风车型，并考虑它们有多少拆法。可以看到这样的拆法总数就等于$|S|$。如果面积为$p$的风车型中有$N$个是“十字”且有$M$个不是“十字”，那么显然有$|S| = N+2M$。假设我们只关心$|S|$的奇偶性，那么我们只需要考虑$N$——换句话说，可以忽略掉所有不是“十字”的风车型，只考虑“十字”。

注意到“十字”的面积一定是$(4z+1)x$。如果$p$是质数且等于$(4z+1)x$，那么一定有$x = 1$且$4z+1 = p$。也就是说，“十字”的个数恰好有一个，即$M=1$。

于是我们证明了$|S|$是奇数，原命题得证。

Bonus：用风车型也可以给出勾股定理的一个“无字”证明，如下图。（这是在我引用的视频里面截的。）你能读懂它吗？