Exactly 7 剧透

Exactly 7是matrix67大大写的一个小游戏，最近无聊所以玩了玩。

剧透预警！SPOILER ALERT!!!!!

这篇博客里有很详细的剧透！！！！！

注：关卡的算分标准是我尝试了若干次之后猜的，可能不准确。

注2：一般的浏览器中，右键单击“在新标签页中打开”可以查看大图。

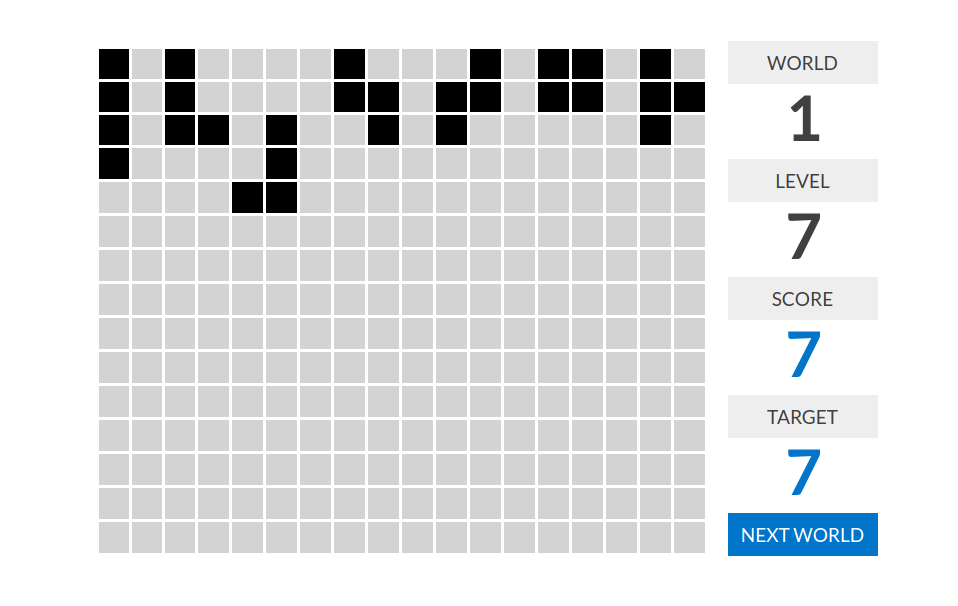
world 1

level 1：分数=黑点的个数

level 2：分数=边界上黑点的个数

level 3：分数=最大黑色四连通块大小

level 4：分数=白色四连通块个数（不算最大的那个）

level 5：分数=最大的$n$使得存在$n\times n$的全黑正方形

level 6：分数=两个黑点之间的$\ell_1$距离（曼哈顿距离）的最大值

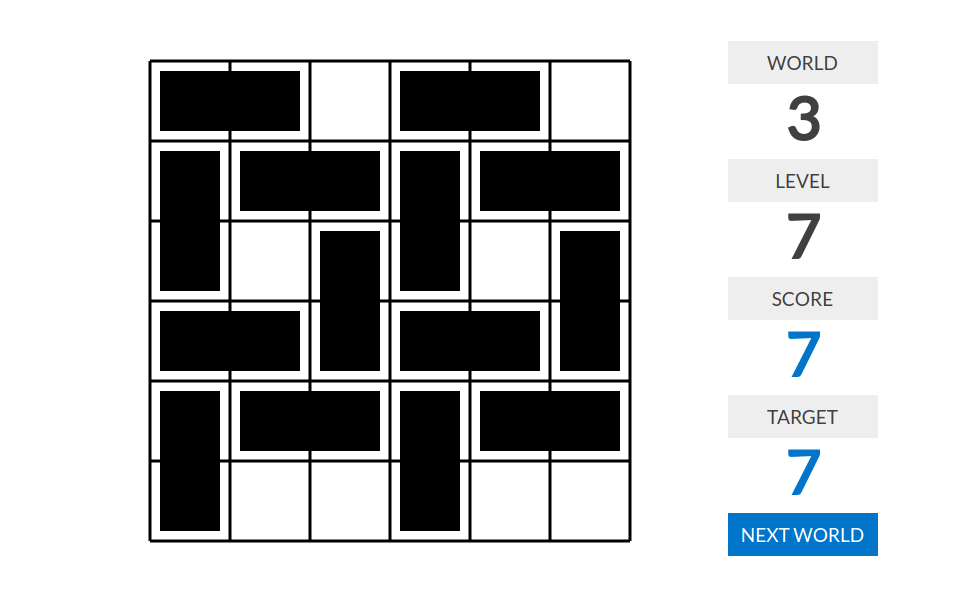
level 7：分数=不同的俄罗斯方块的个数

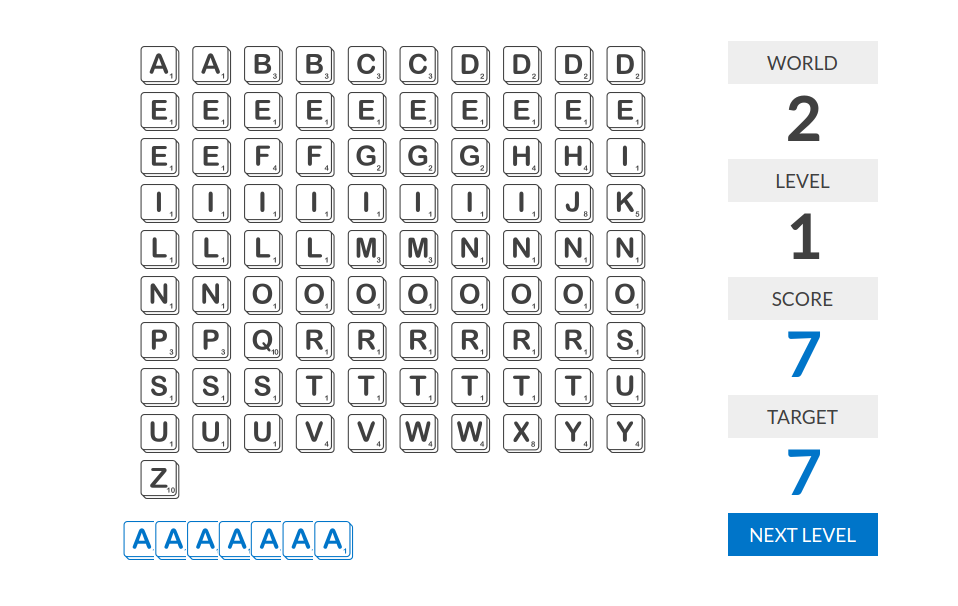
world 2

level 1：分数=字符数量

level 2：分数=BCMP的数量（方块右下角的数字是$3$的四个字母）

level 3：分数=还剩下的字母中，恰好剩下三个的字母数量。（比如说因为总共有$6$个N，所以如果你的字符串用了$3$个N那么分数加一；因为总共有$3$个G，所以如果你的字符串没有用G那么分数加一。）

level 4：分数=最长的形如AABBCCDD的子串的长度除以$2$。换句话说，这个子串第$2i-1$位和第$2i$位总是相等，但是第$2i$位和第$2i+1$位总是不相等。

level 5：分数=最长的形如GFEDCBA的子串的长度。换句话说，后一个字符总是比前一个字符恰好少一。

level 6：分数=字符串中出现了两次、且两次位置没有重叠的最长子串的长度。

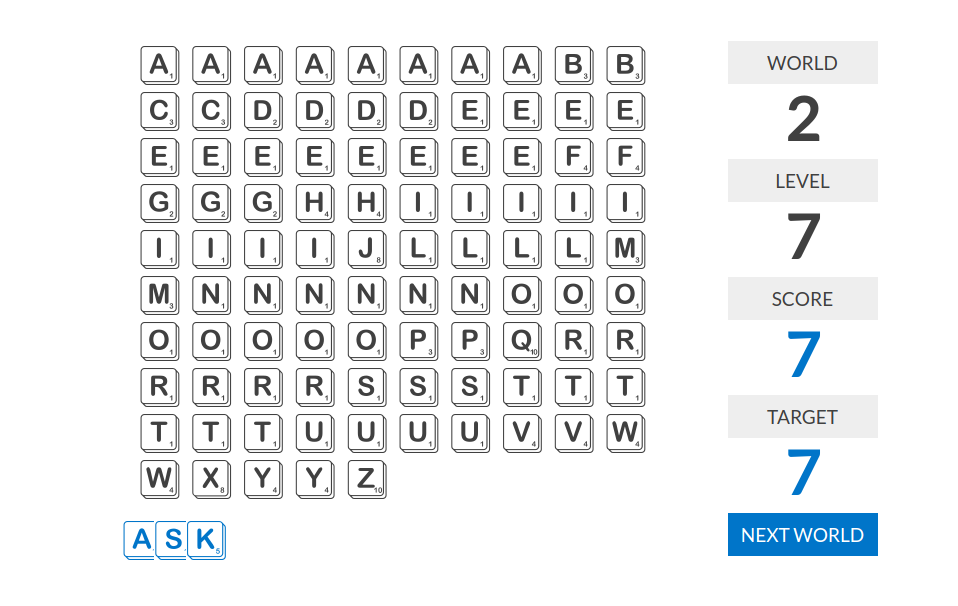
level 7：如果字符串组成了一个英文单词，那么分数=所有字母右下角的数字之和；否则分数为$0$。

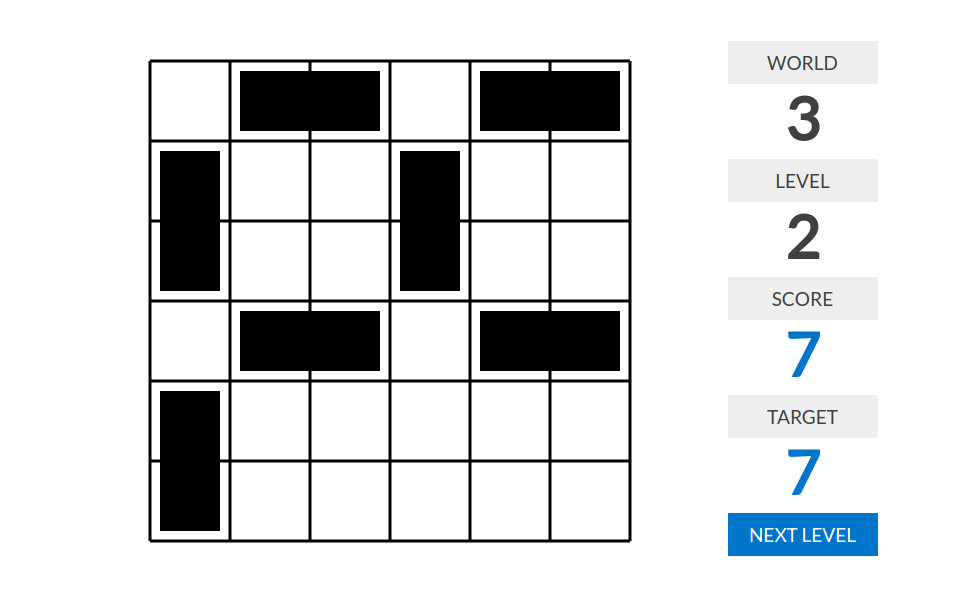
world 3

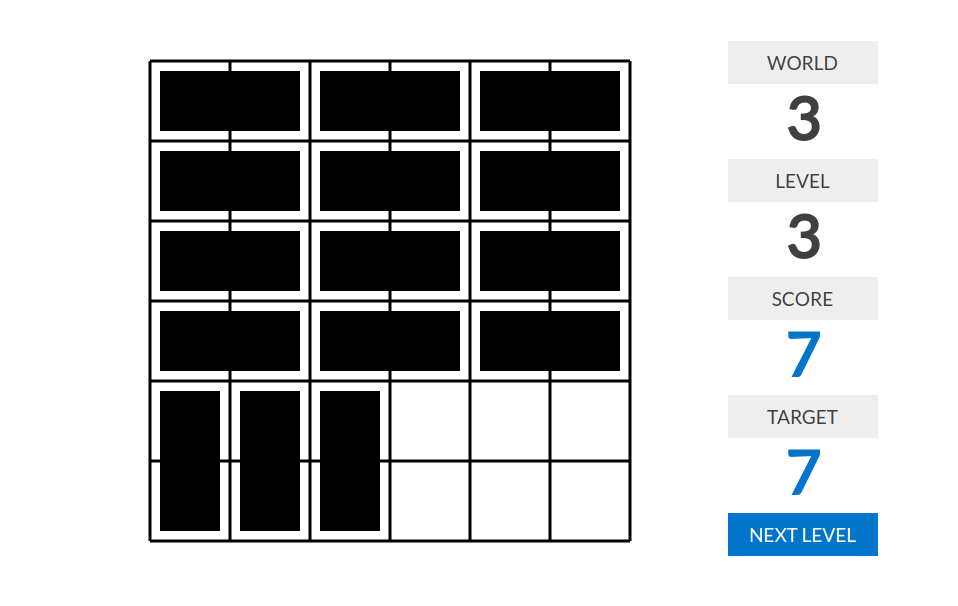
level 1：分数=多米诺骨牌数量

level 2：分数=交错的多米诺骨牌对的数量。一对骨牌是交错的，当且仅当它们有公共端点但没有公共边，且公共端点处的骨牌只有它们两个。

正确示例：      

错误示例：     

level 3：分数=完全被多米诺骨牌覆盖的行或列的数量

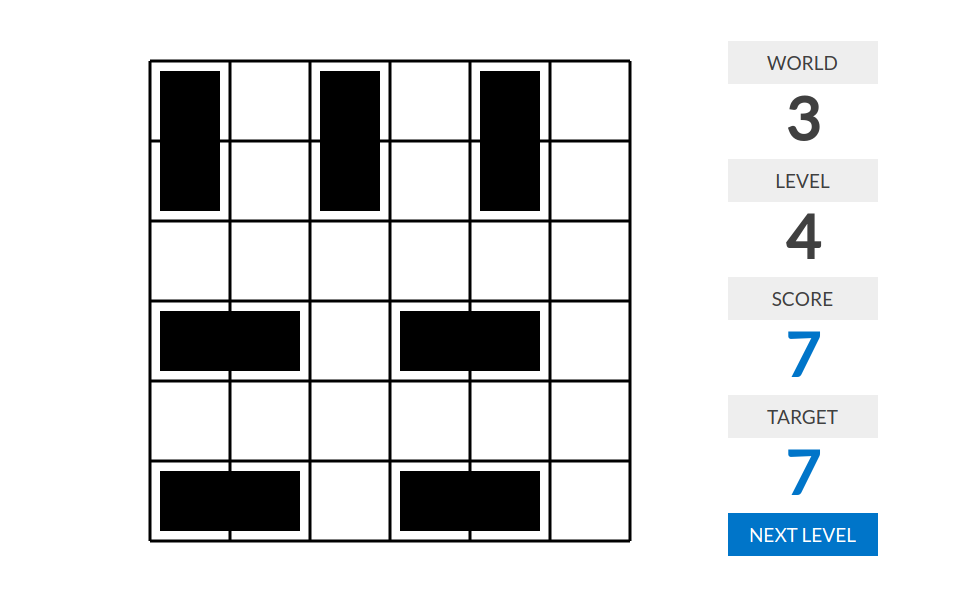
level 4：分数=独立于其他多米诺骨牌的骨牌数量。这里“独立”的意思是不和任何其他多米诺骨牌相邻（包括有公共端点的情况）。

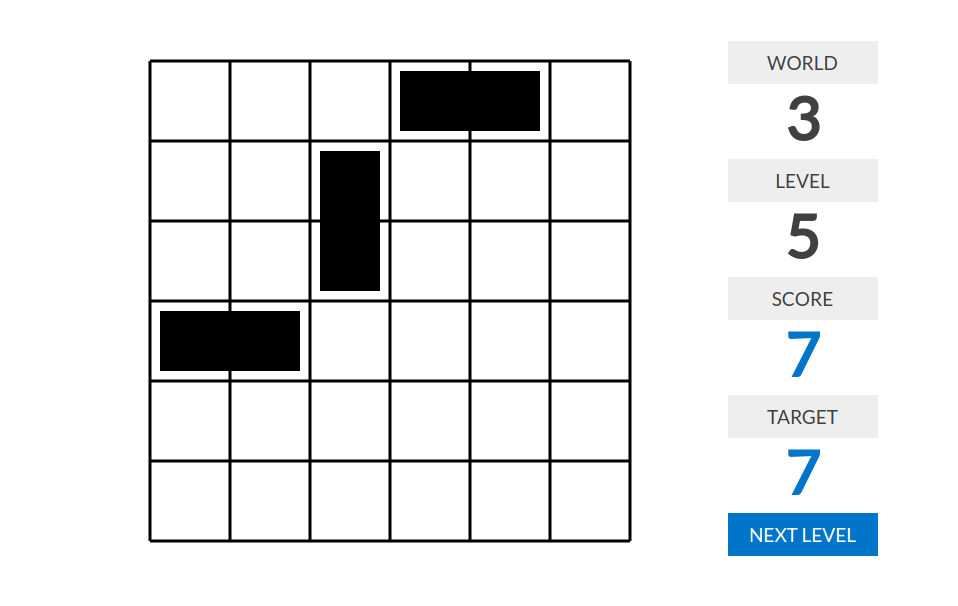
level 5：分数=左上角白色格子所在的四连通块的大小。（如果左上角格子是黑的，即该格子被多米诺骨牌覆盖了，那么分数为$0$）

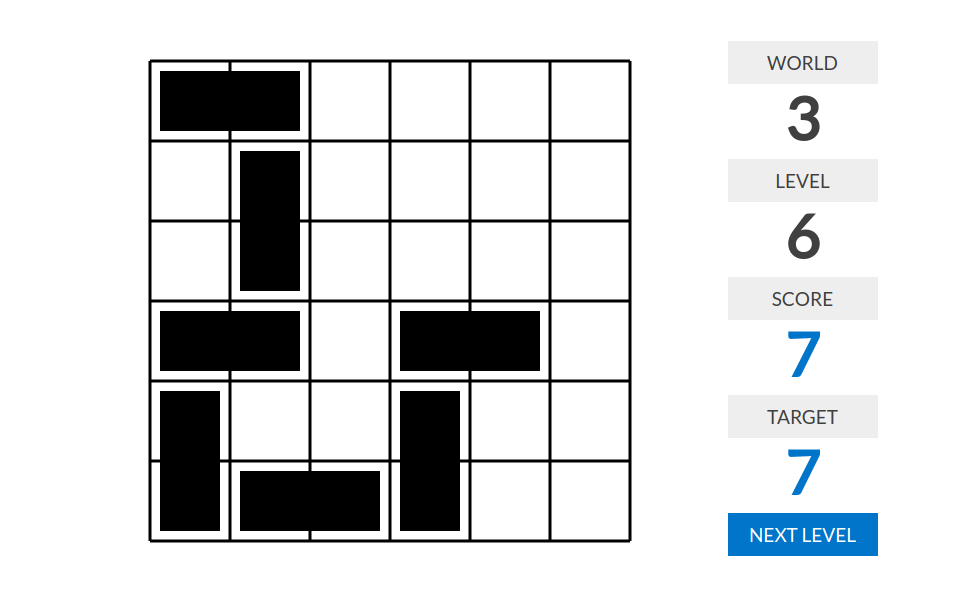
level 6：分数=最长链中多米诺骨牌横竖交替的次数。这里，一条链是指一个黑色四连通块，使得除了“链头”和“链尾”的两张骨牌只和一张骨牌四连通以外，其他骨牌都恰好和两张骨牌四连通。

例子：这条链的横竖交替次数为$4$。

level 7：分数=满足以下条件的多米诺骨牌对的数量。这两张骨牌之间恰好夹着一个$2\times 2$正方形，且这个正方形内部不能有位置恰好“平行”的骨牌。（见错误示例。。。）

正确示例：          

错误示例：（中间夹的不是$2\times 2$）     （中间夹了一个位置“平行”的骨牌）

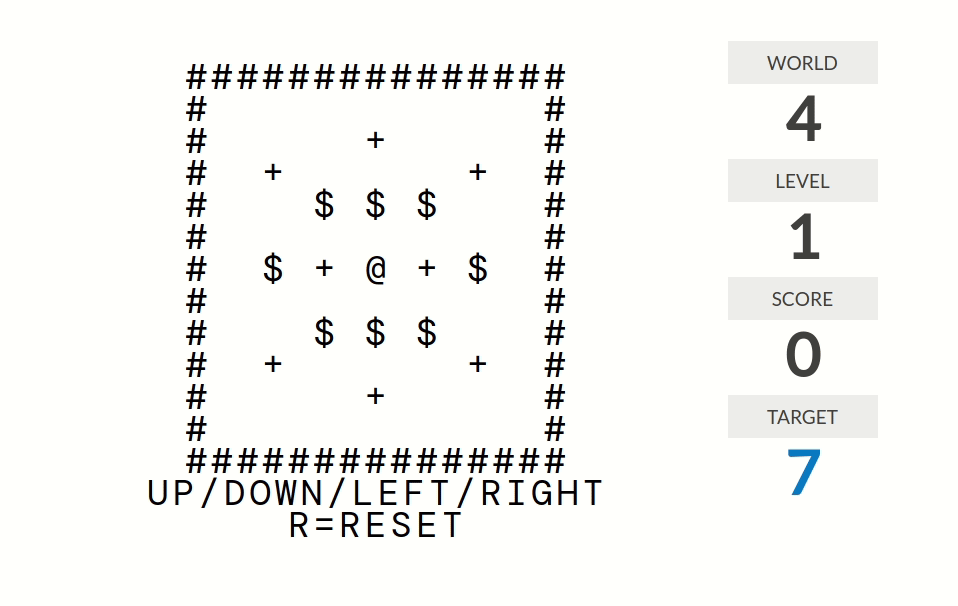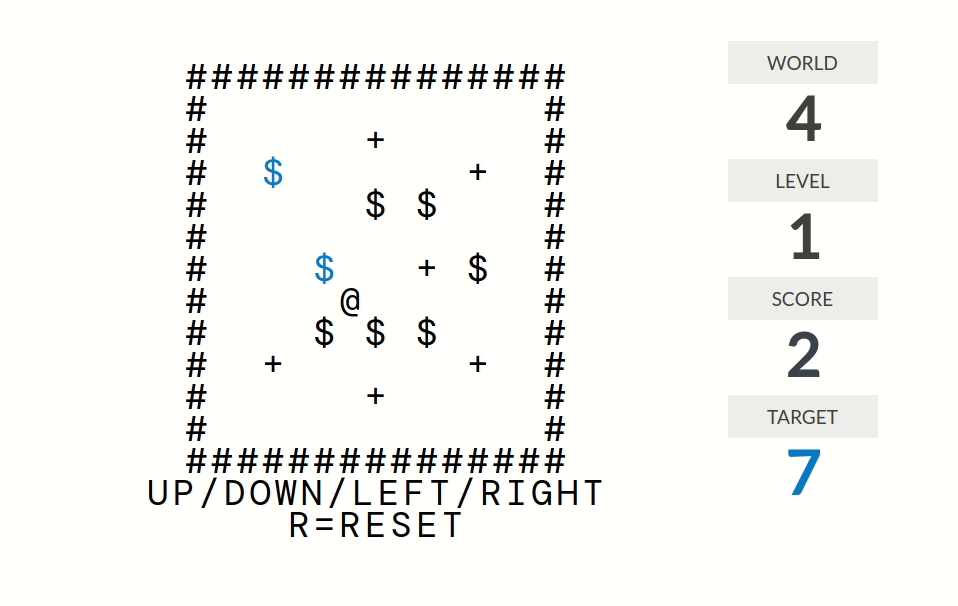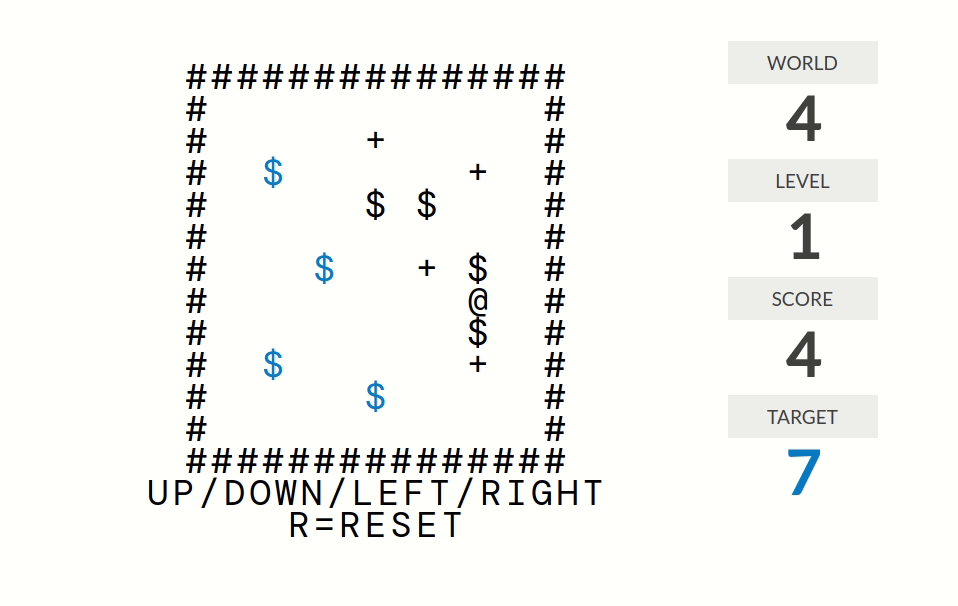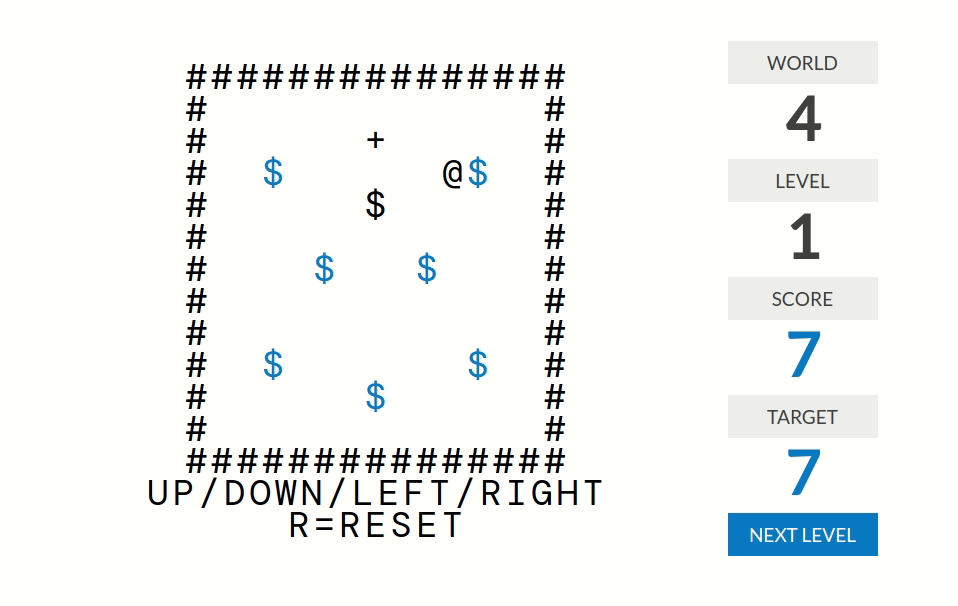
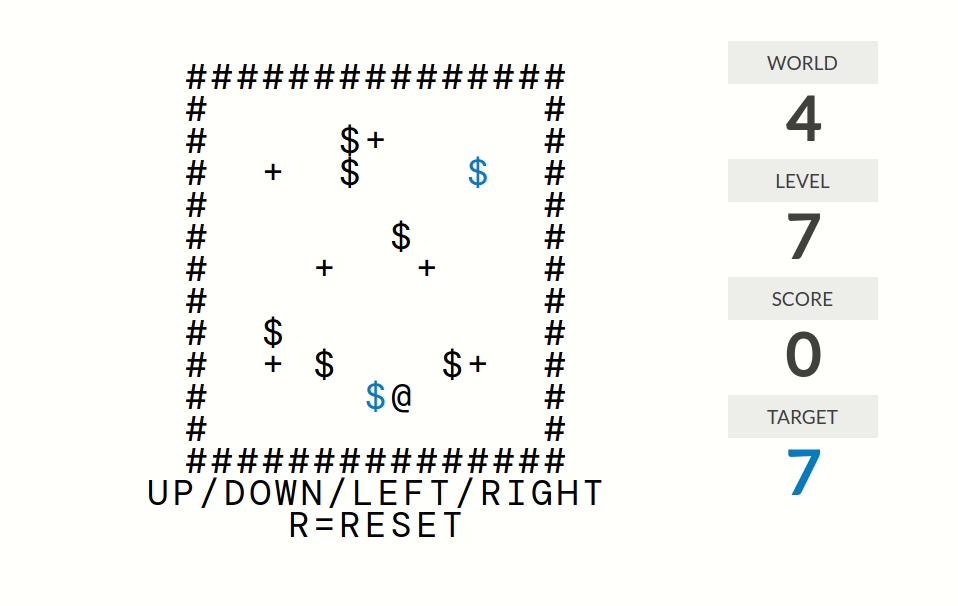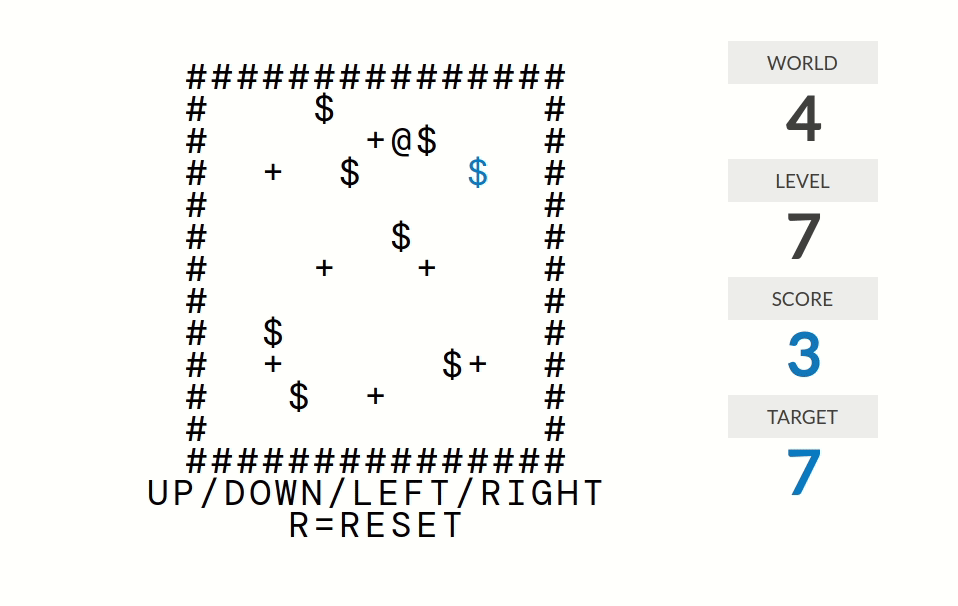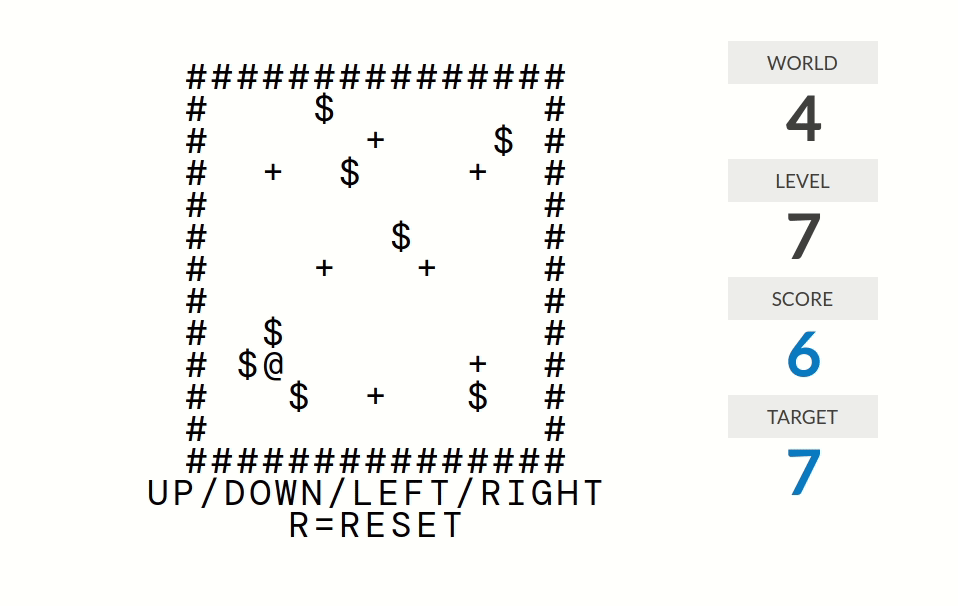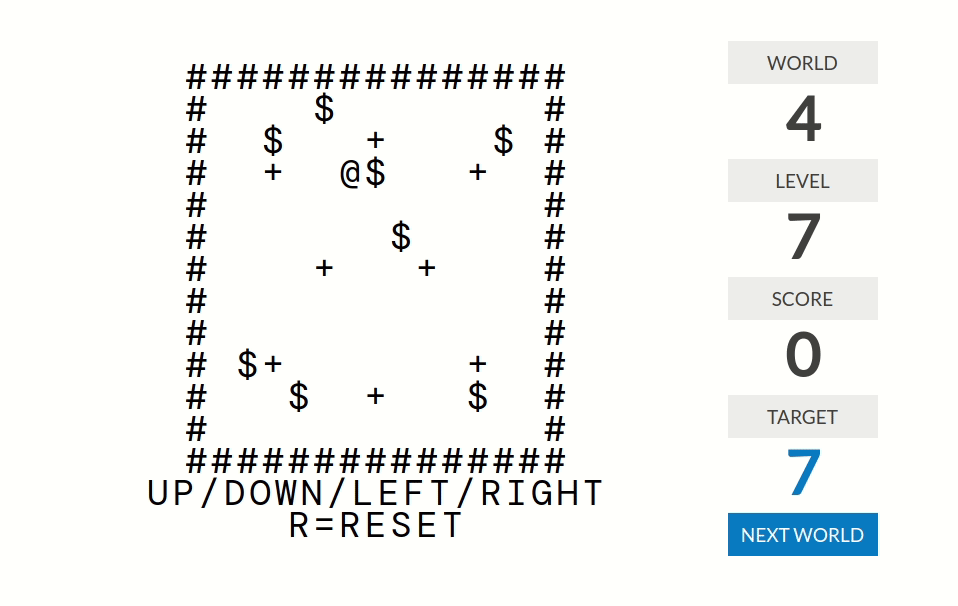
world 4

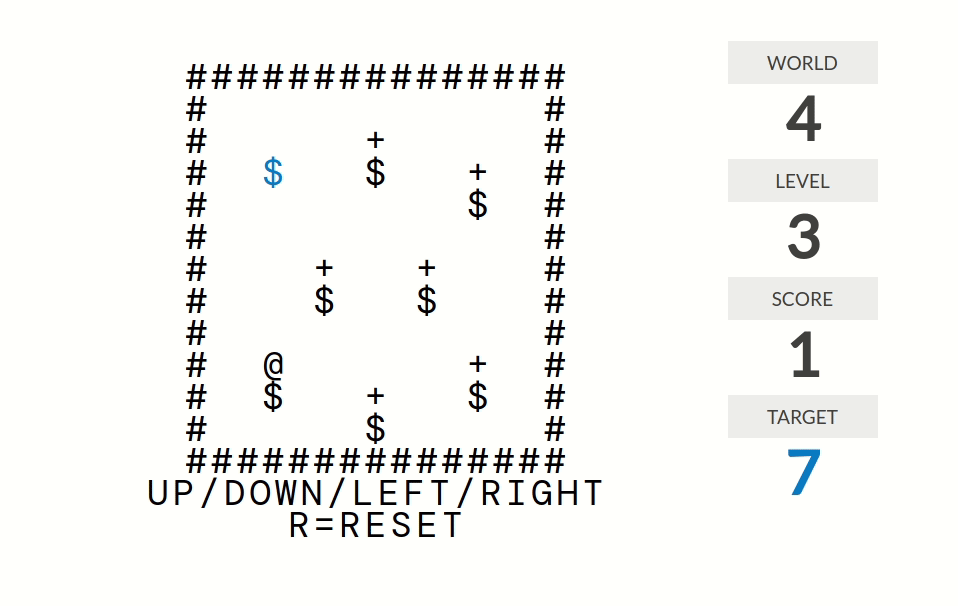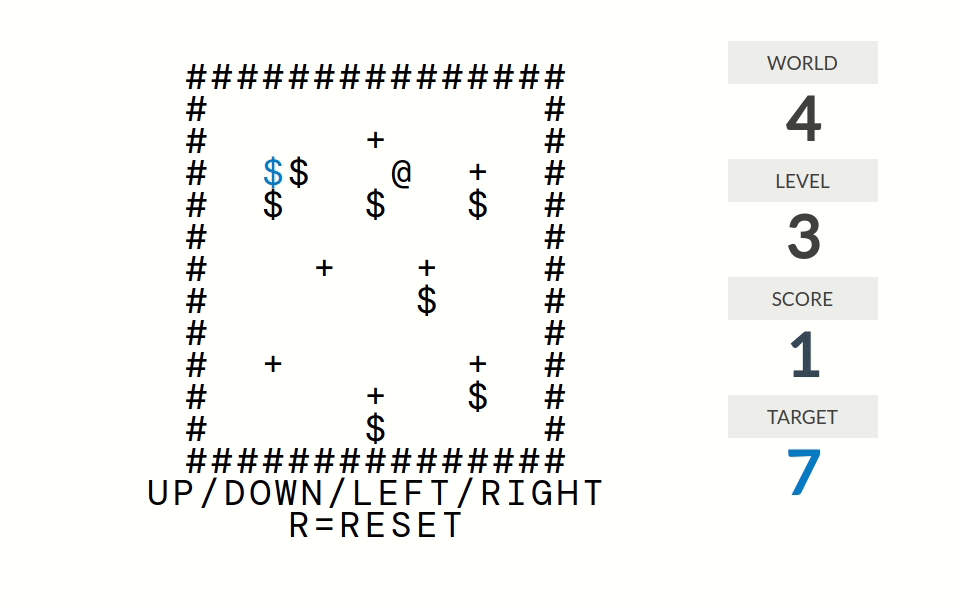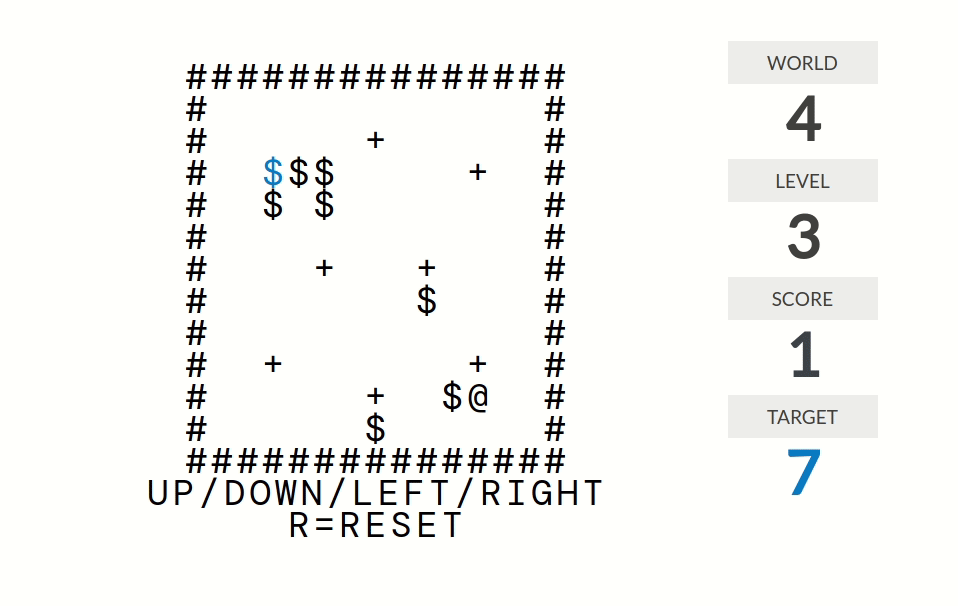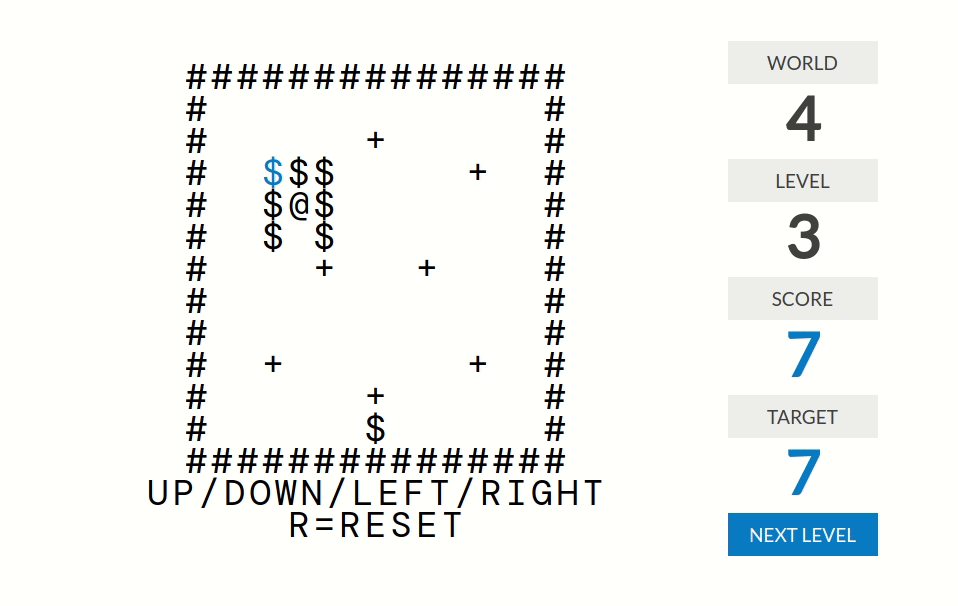
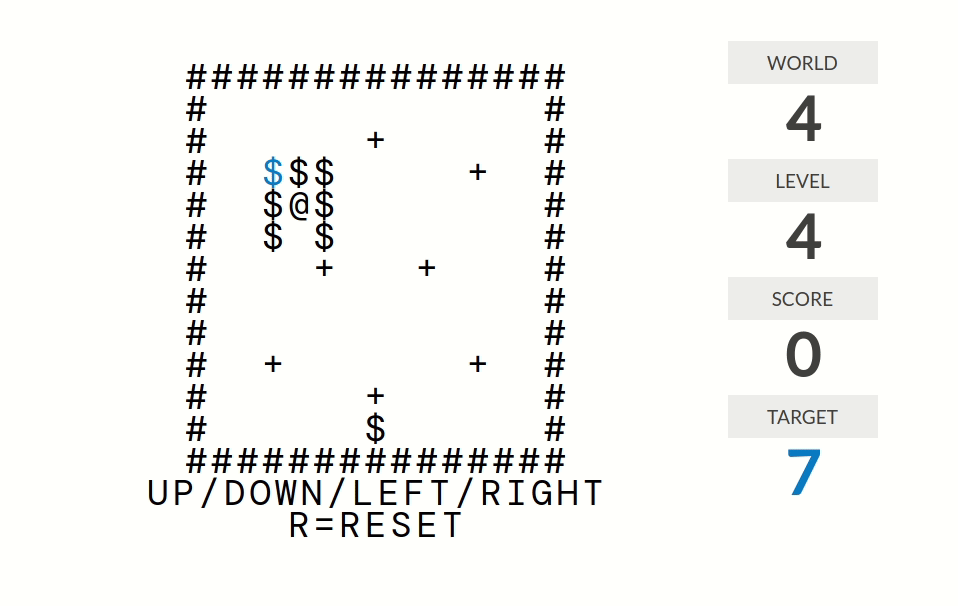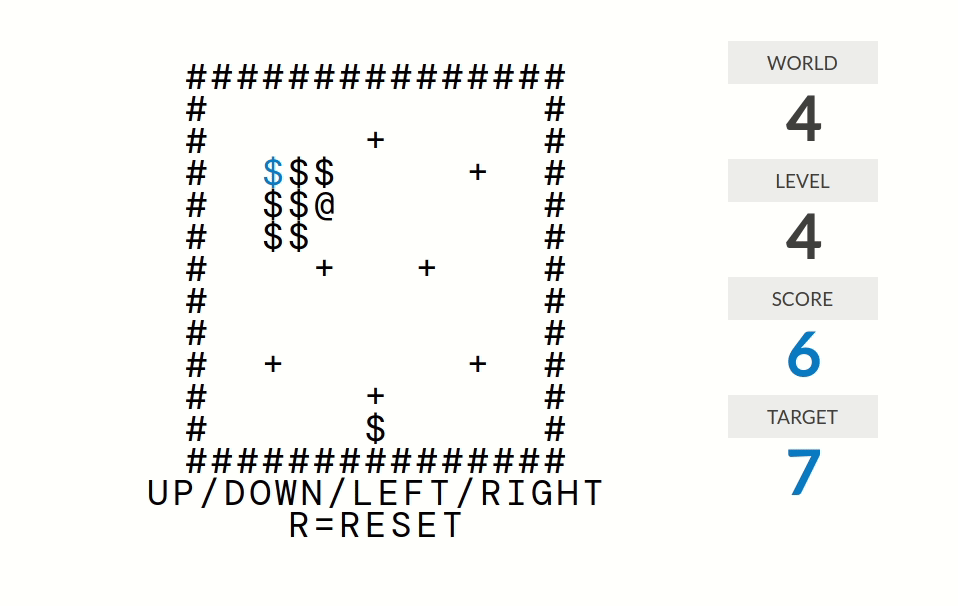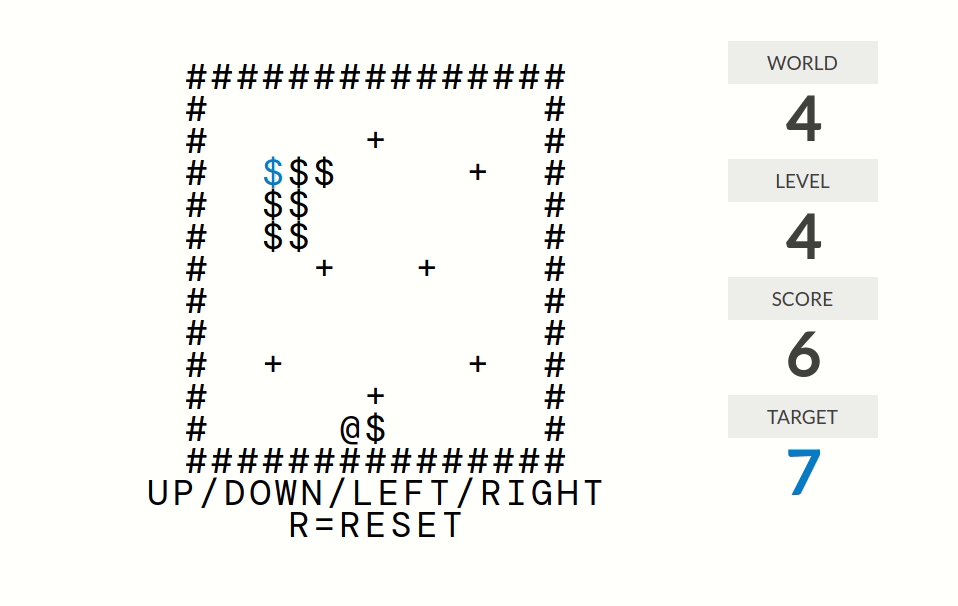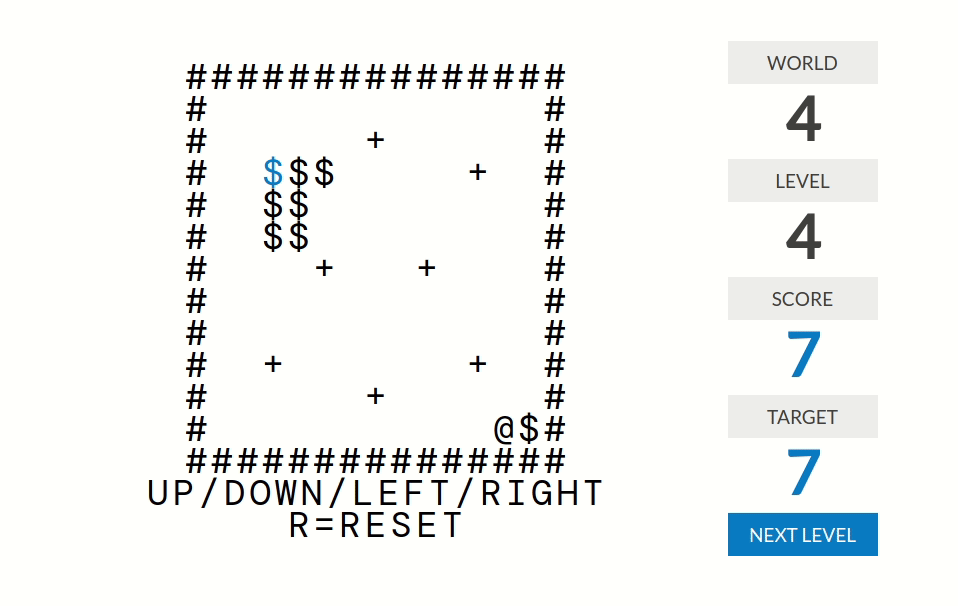
level 1：分数=被推到正确位置（某个+号）的箱子（$）的个数

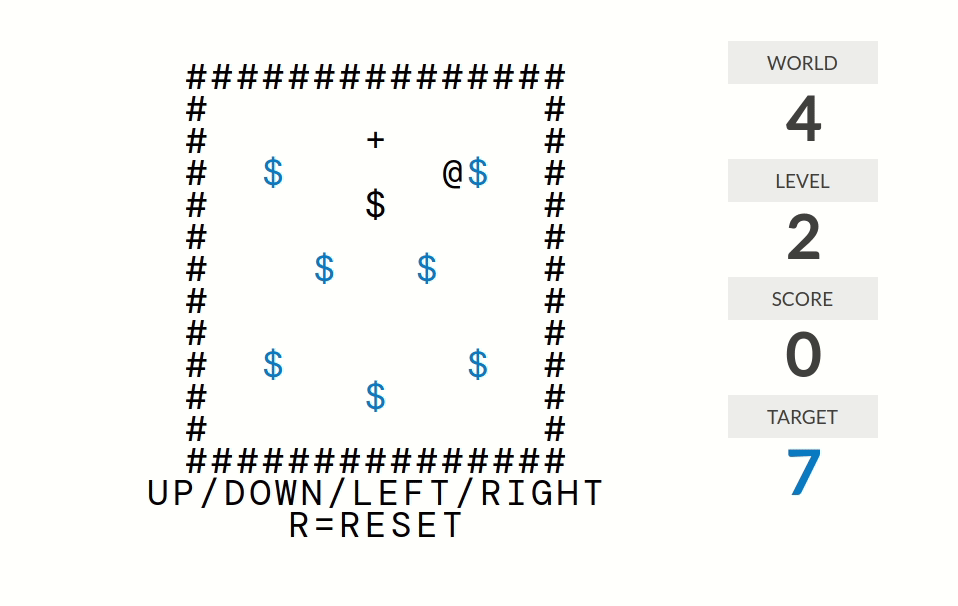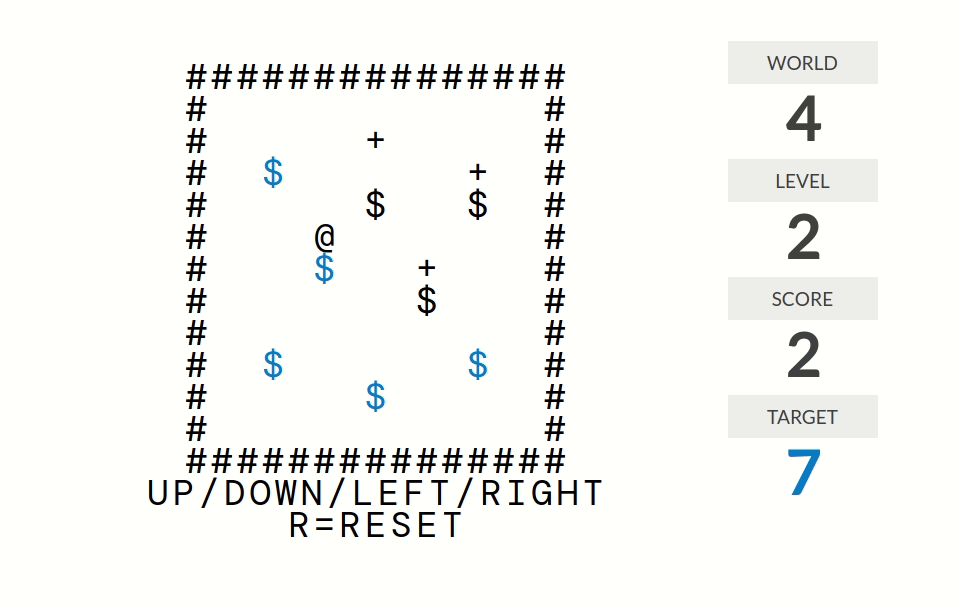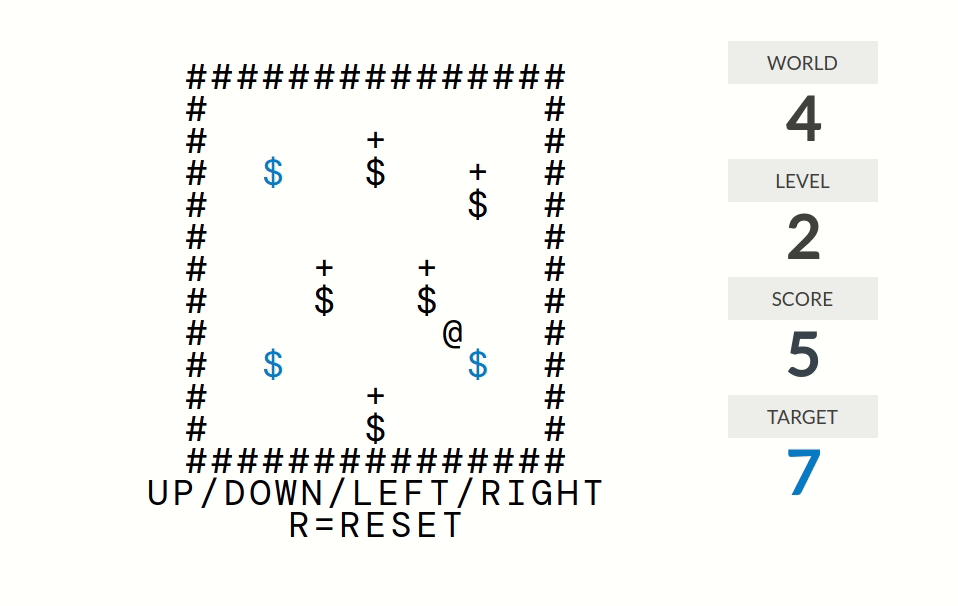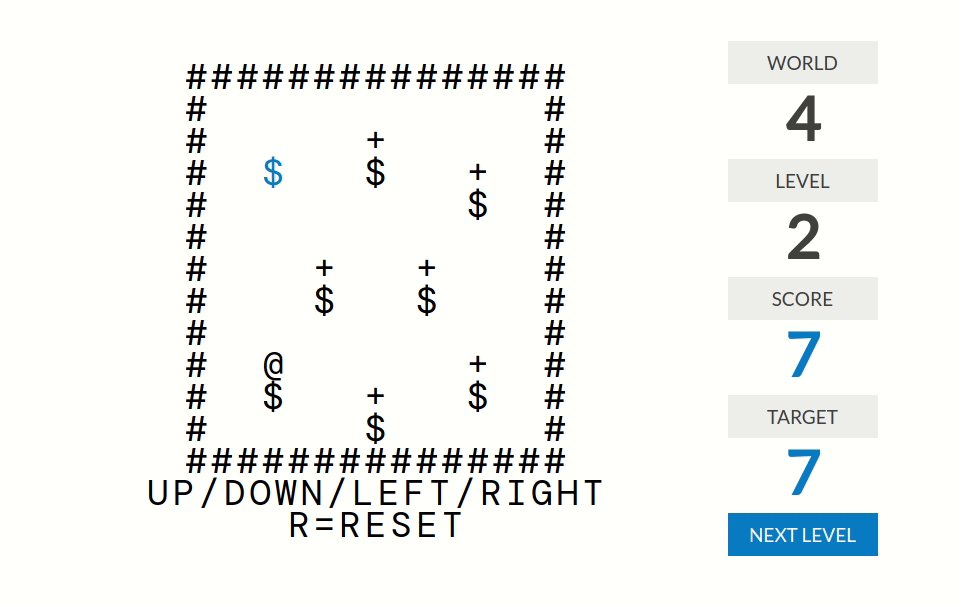
level 2：分数=在某个+号恰好下面一格的箱子个数

level 3：分数=@周围八个格子中$的个数

level 4：分数=位置无法被改变了的箱子的个数。比如说如果一个箱子被推到墙角，那么它的位置就是无法被改变的；如果四个箱子排成了$2\times 2$的形状那么它们的位置也是无法被改变的。

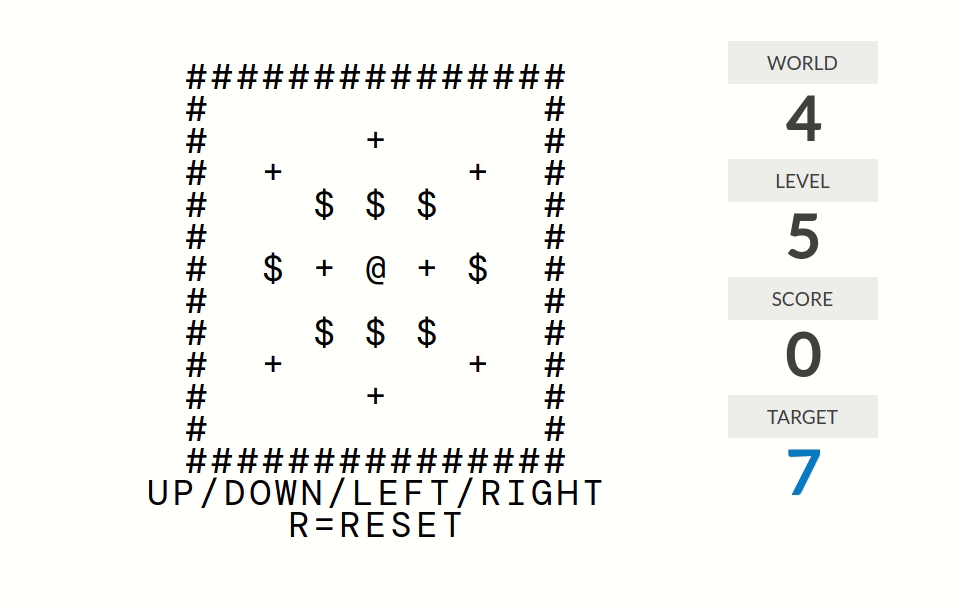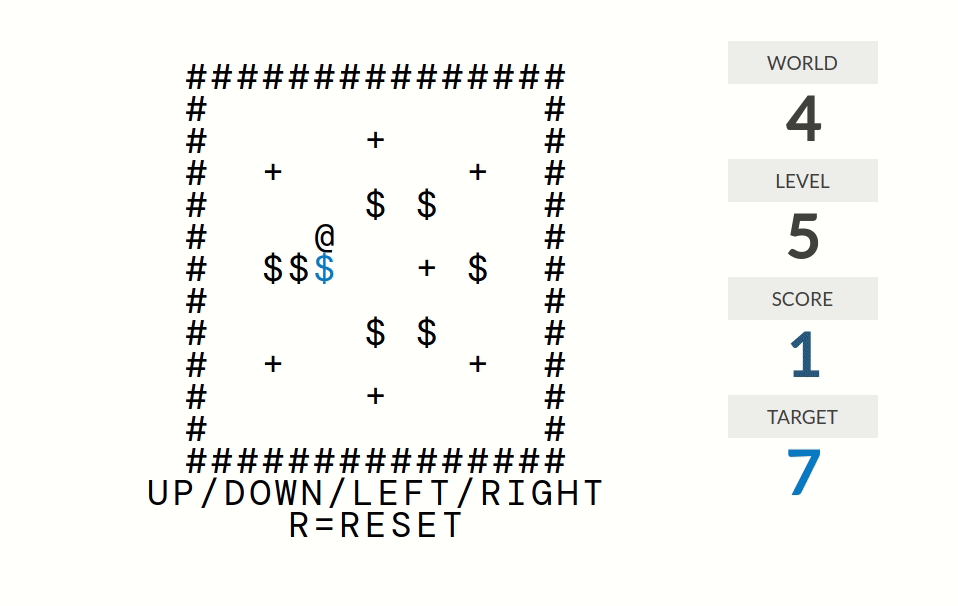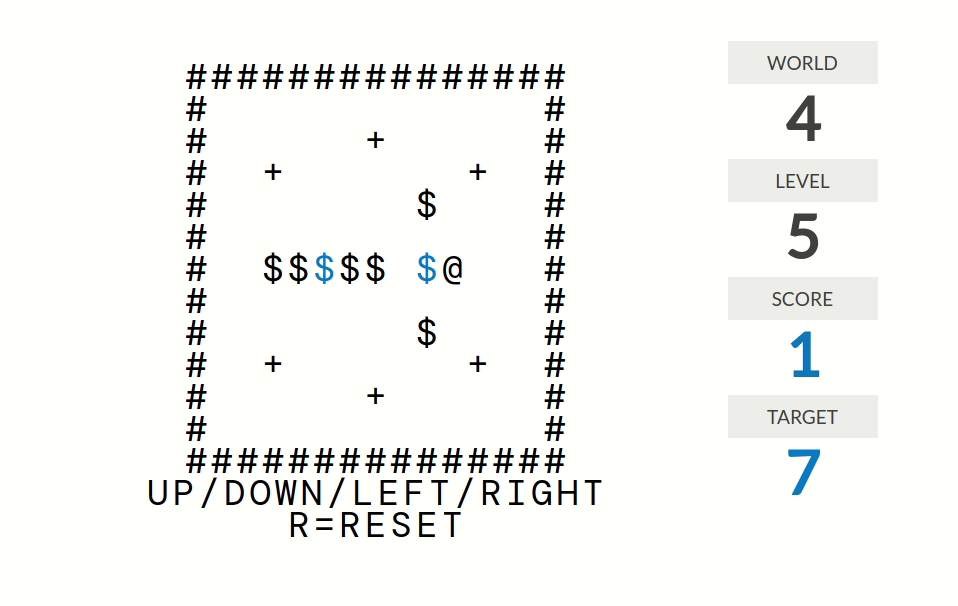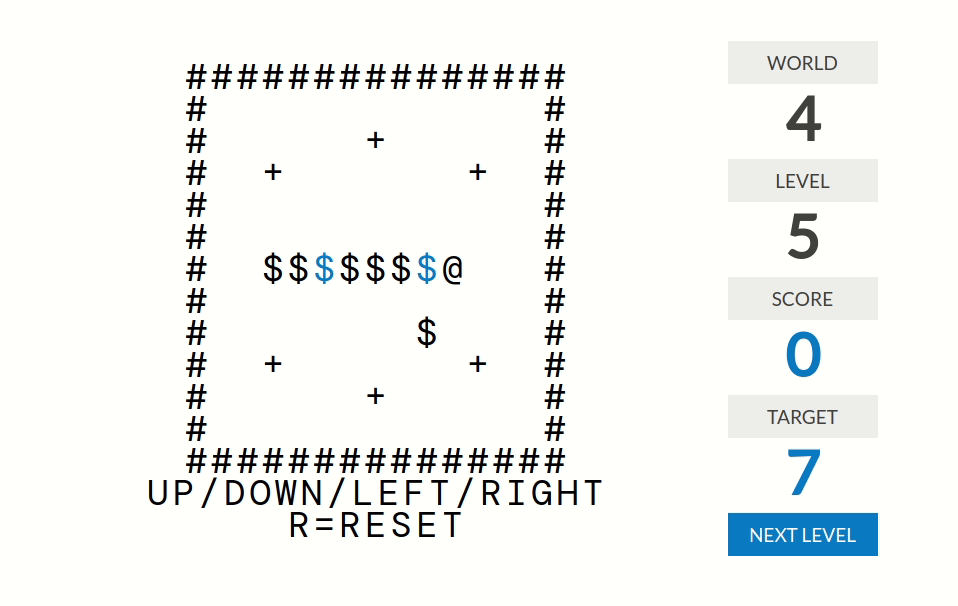
level 5：分数=按键方向的箱子个数。例如如果你走一步路那么分数为$0$；如果你推了一个箱子那么分数为$1$；如果局面形如@$$$（@是你，$是箱子）且你向右推那么分数为$3$。

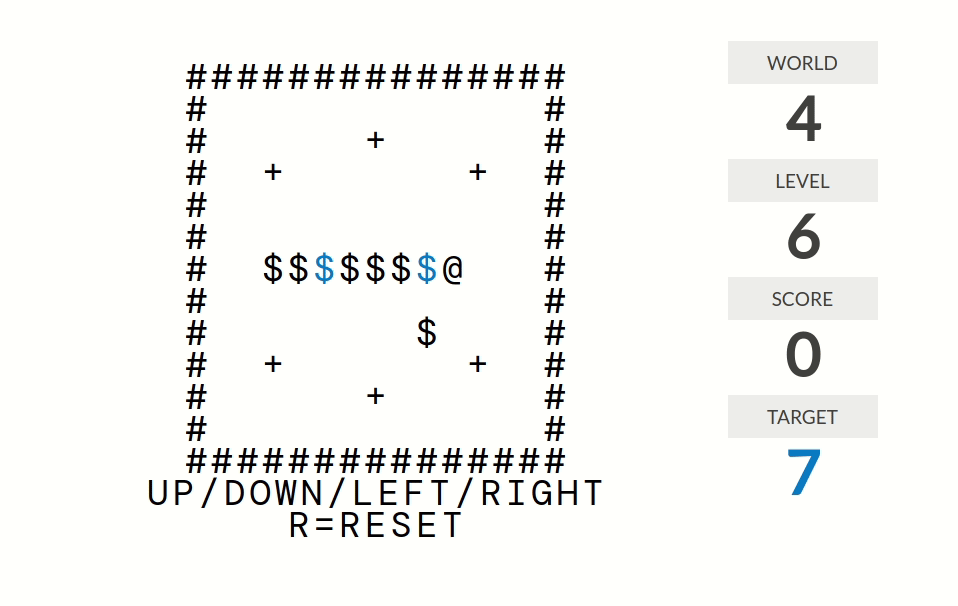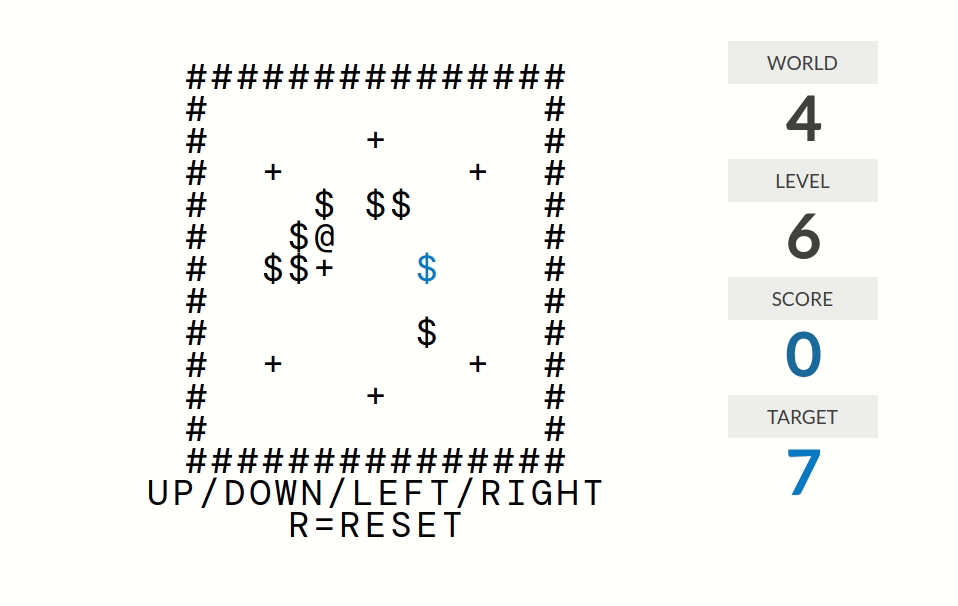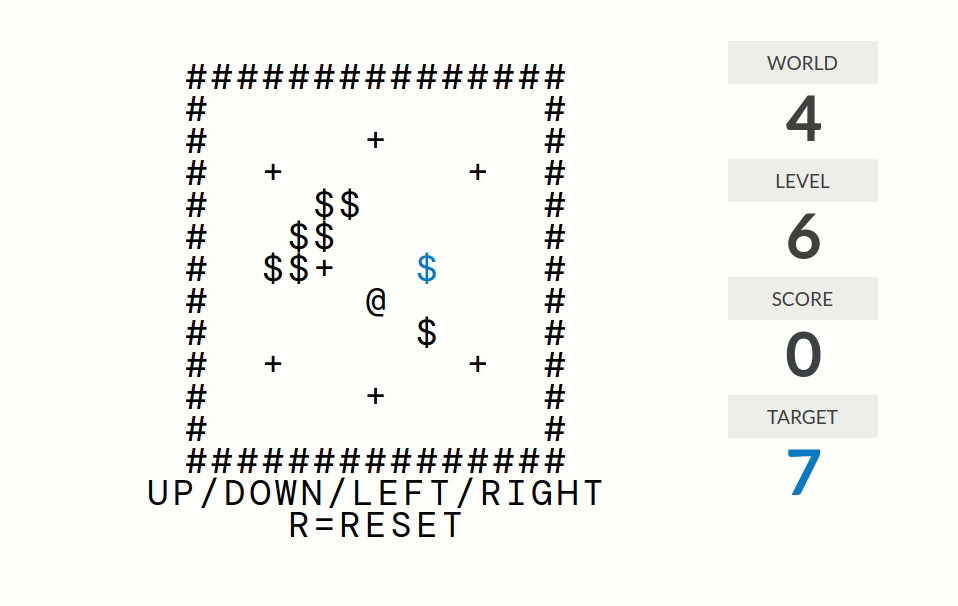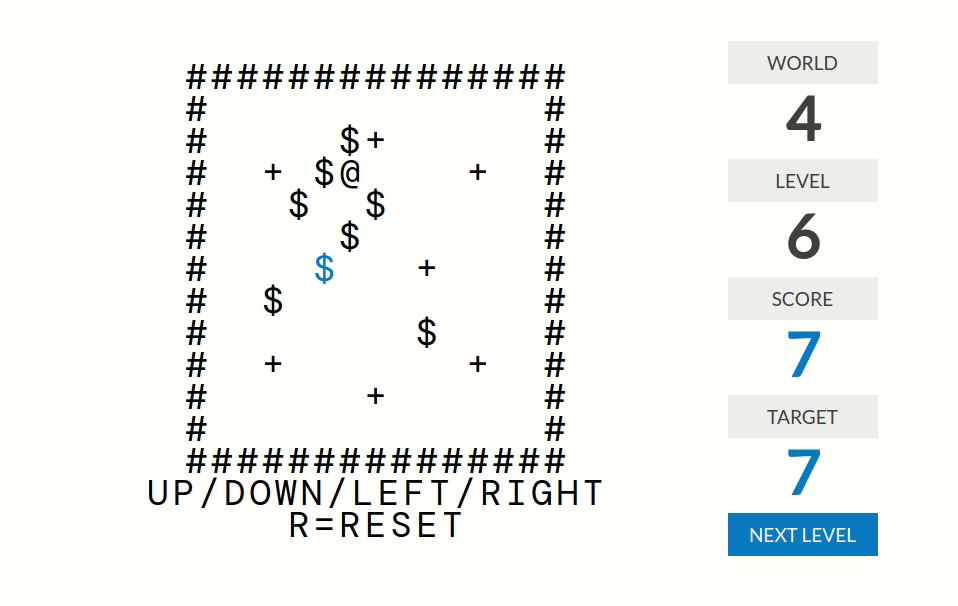
level 6：分数=连续推的箱子个数。例如如果你上上一步推了箱子1、上一步推了箱子2、这一步推了箱子3，那么分数为$3$。

level 7：分数=连续推到+号处的箱子个数。更准确地说，分数是这样计算的：走路（但是不推箱子）时分数归零；推箱子时分数不变；箱子经过一个+号时分数加一。

world 5

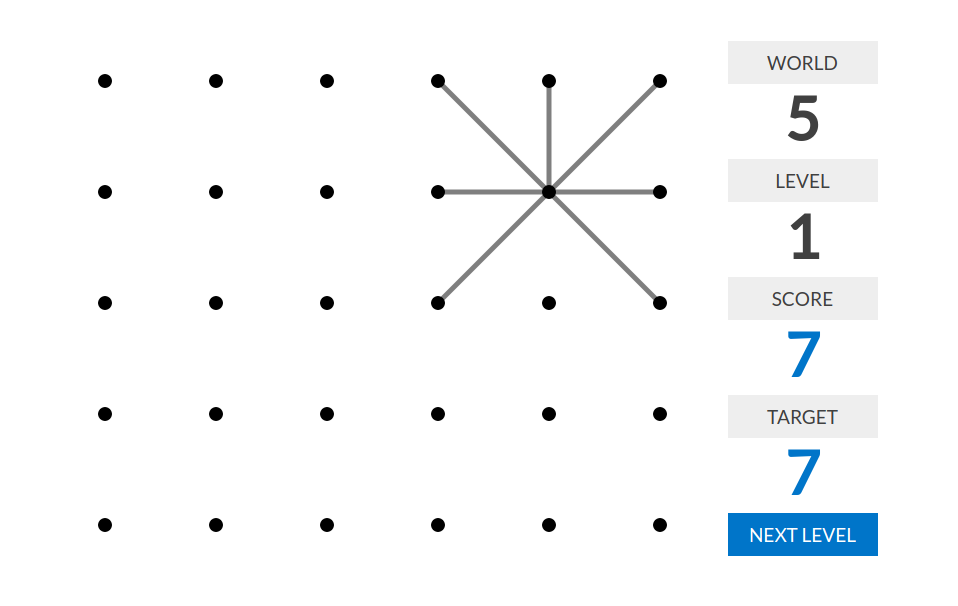
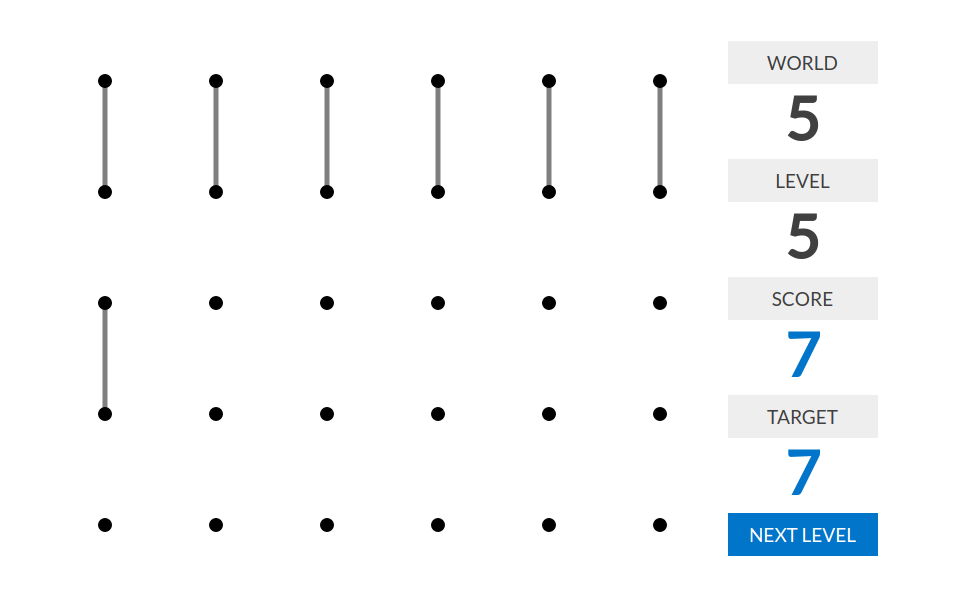
level 1：分数=线段的数量

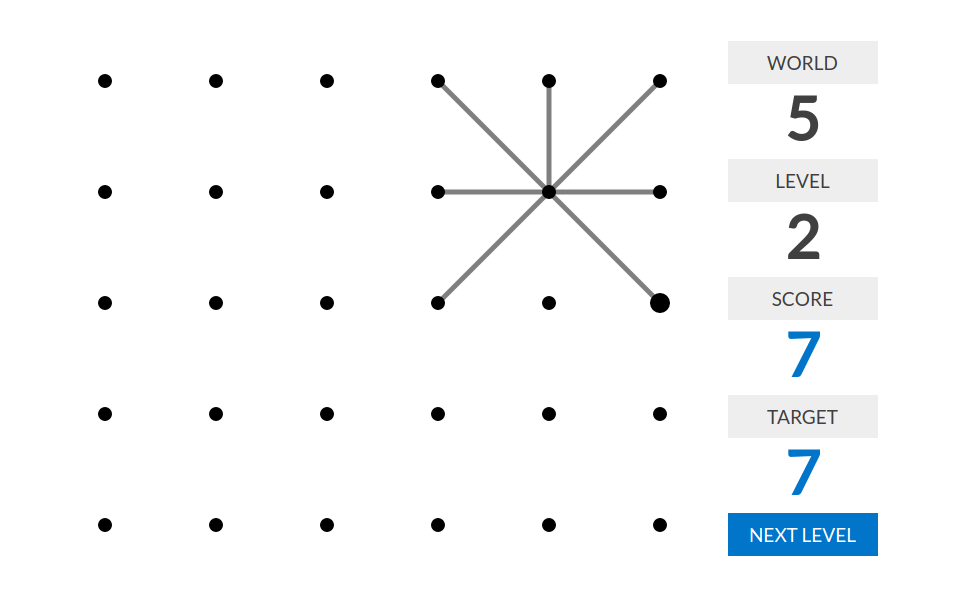
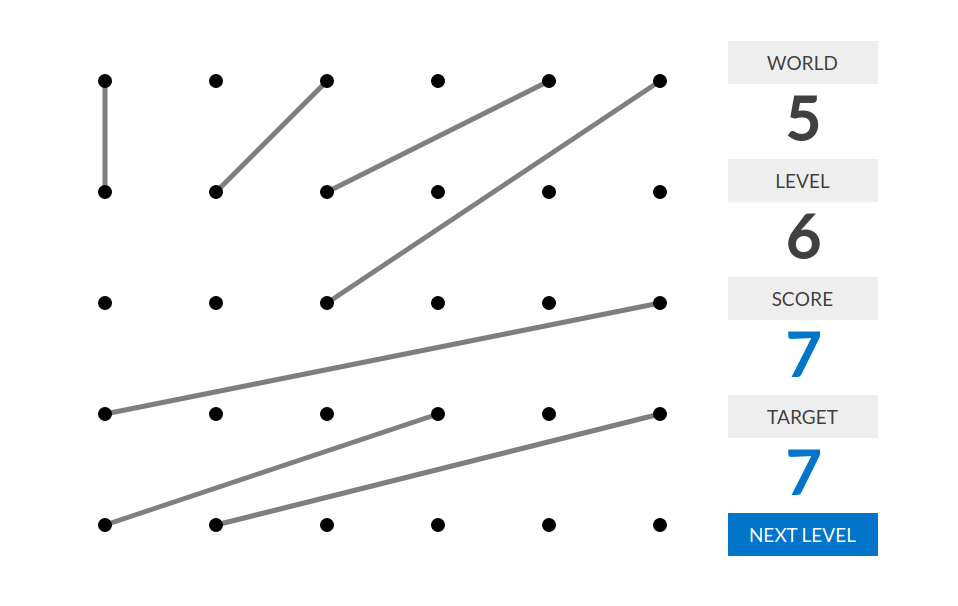
level 2：分数=最大的点的度数

level 3：分数=最长的上下交替的链的长度。例如，一条合法的链中，第一个点（严格）比第二个点低，第二个点（严格）比第三个点高，第三个点（严格）比第四个点低，第四个点（严格）比第五个点高，以此类推。

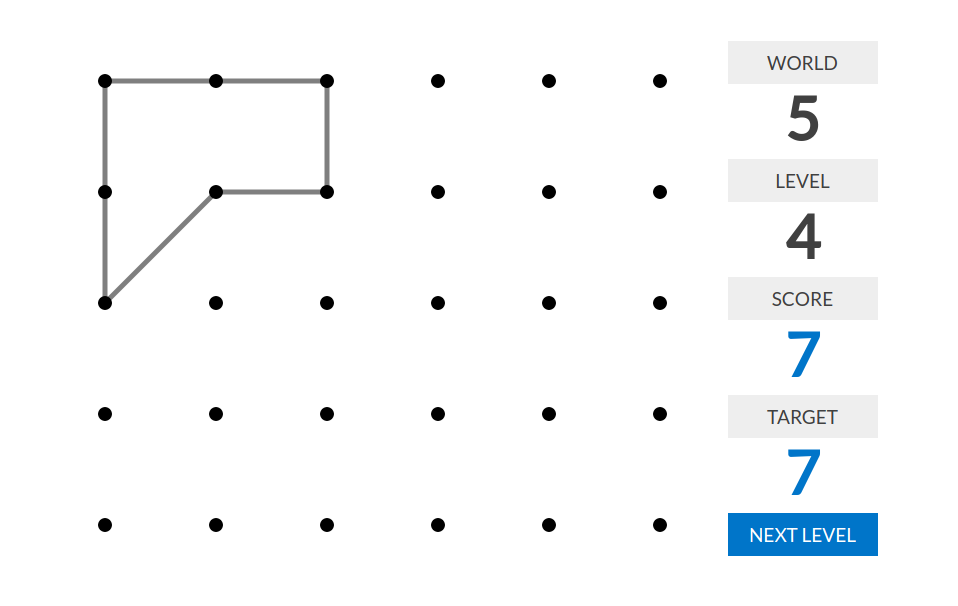
level 4：分数=最大的$n$使得图中存在一个$n$边形。（可以是凹的，但是不能自交。）这个$n$边形必须自己组成一个连通块（也就是不能和其他线段相交）。

level 5：分数=最多的斜率相同的线段的个数。（这些线段不能和任何其他线段相交）

level 6：分数=不同的斜率个数（线段不准相交；$k, 1/k, -k, -1/k$算同一种斜率）

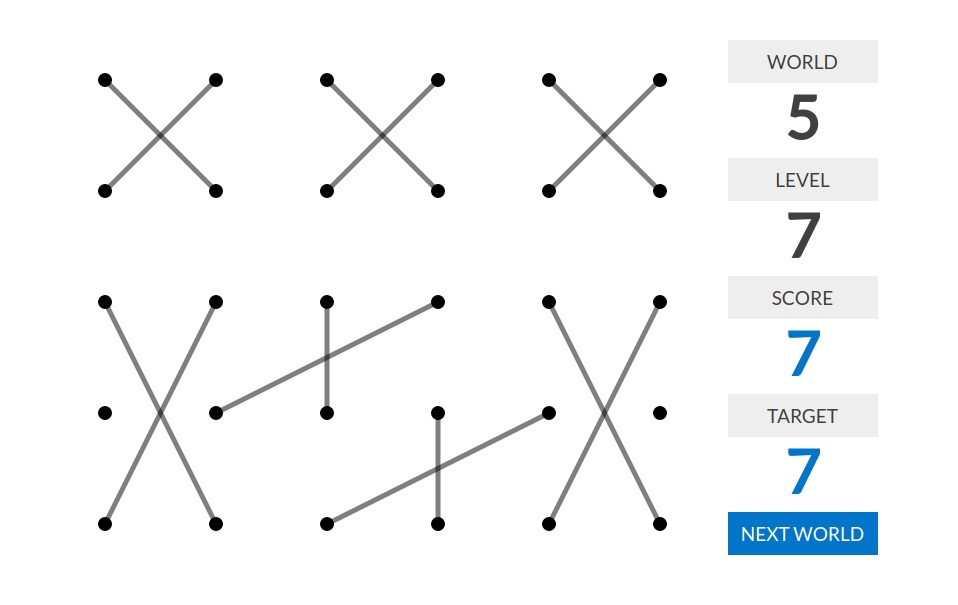
level 7：分数=x的个数。这里一个x指两条直线，它们相交但是不共端点，且它们与其他线段都不相交（即组成一个独立的连通块）。

world 6

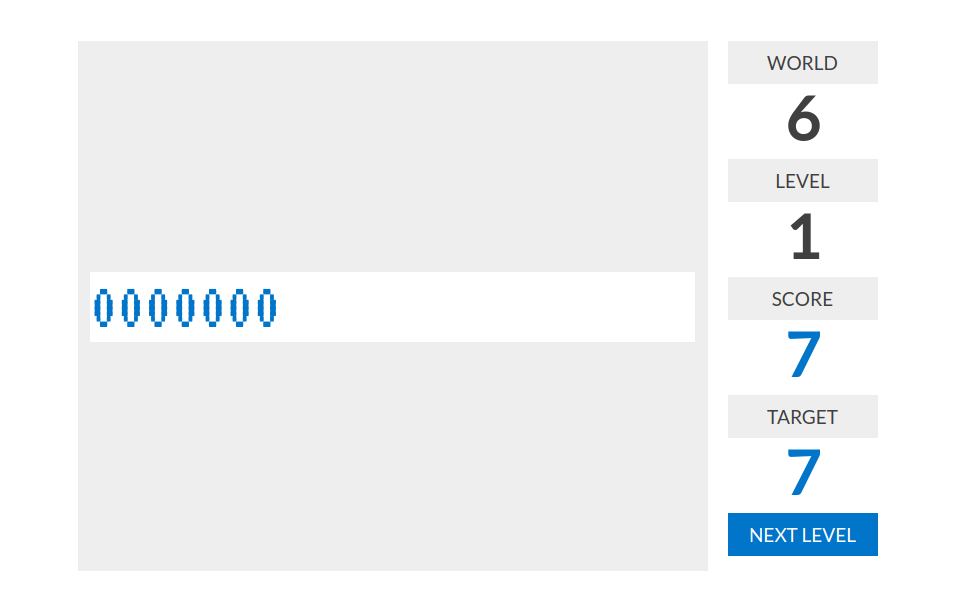
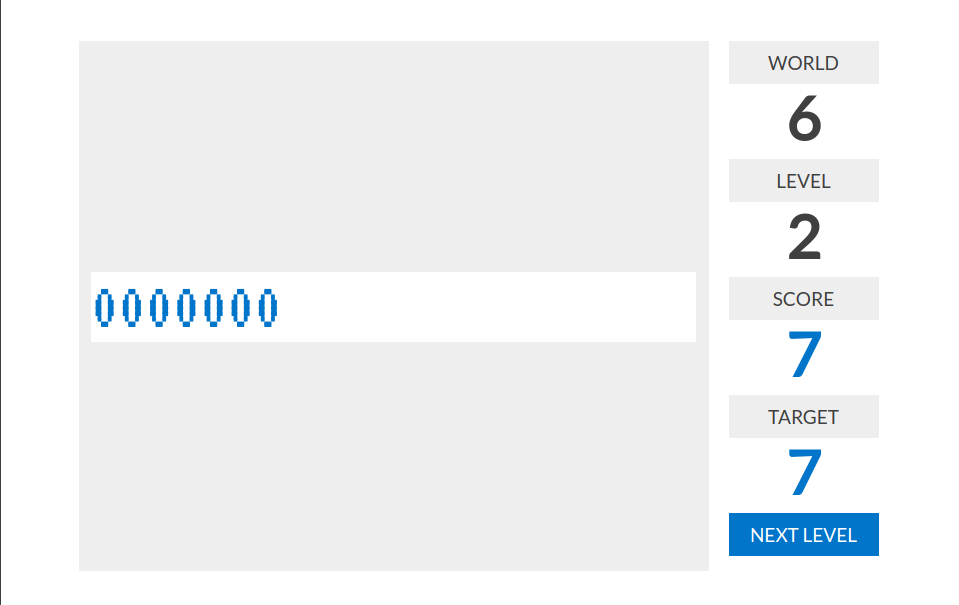
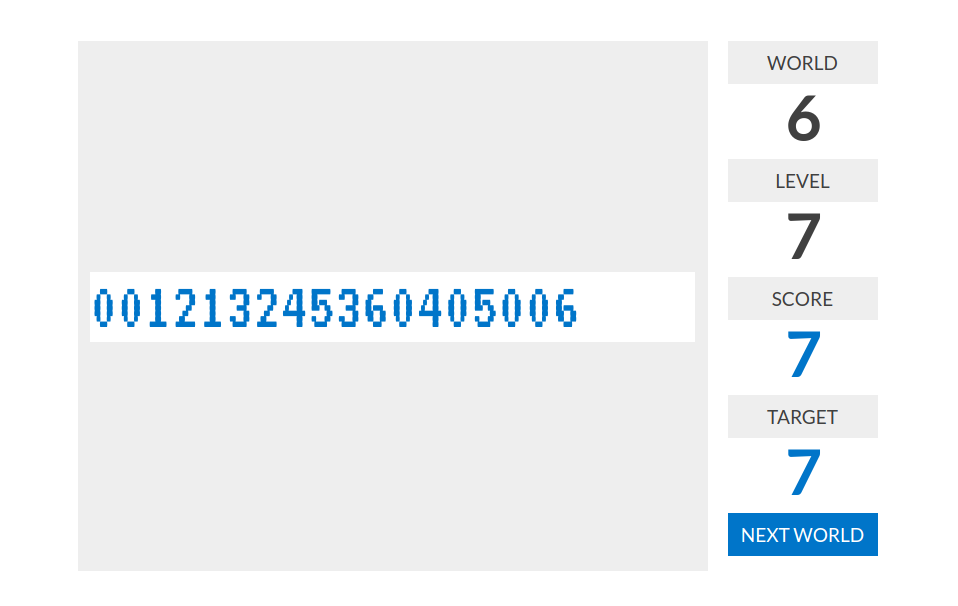
level 1：分数=数字串的长度

level 2：分数=0的个数

level 3：分数=“出现次数等于这个数字本身”的数的个数

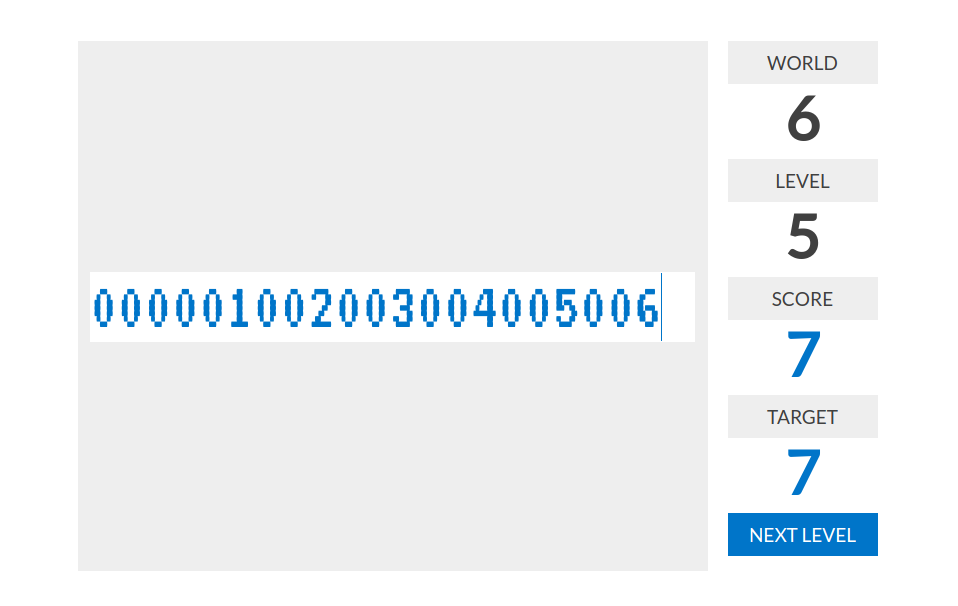
level 4：分数=连续出现的两位数中， 最大那个减最小那个的值。比如说136297的分数是84=97-13

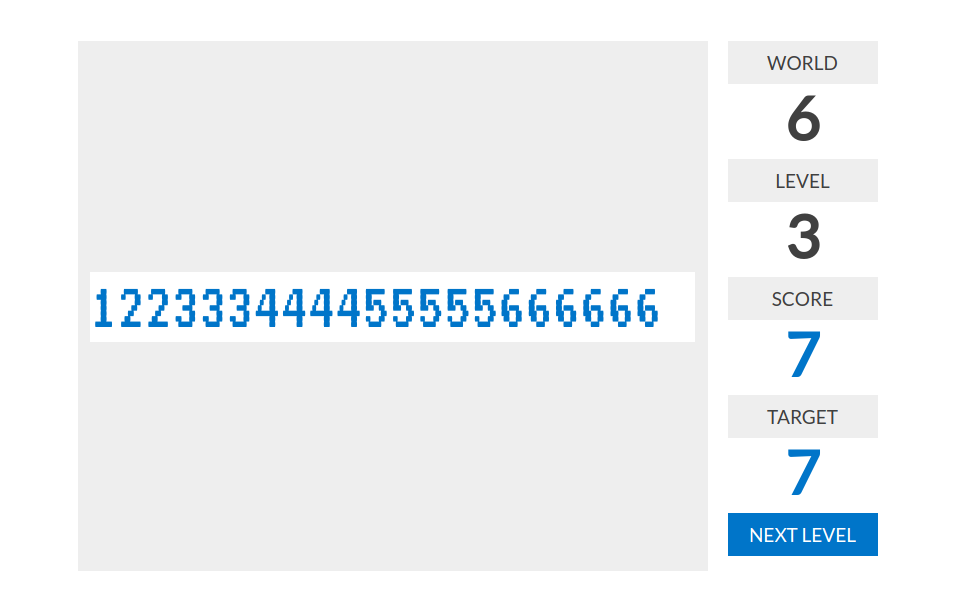
level 5：分数=把整个串划分成长度为3的小块，连续增加1的块数。例如233234235236的分数是4

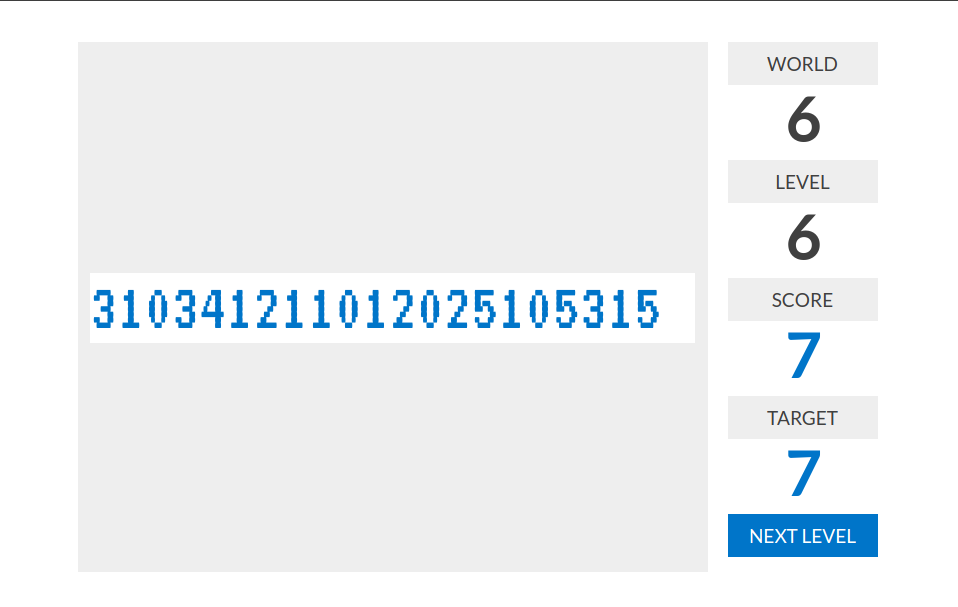
level 6：我不会。。。反正我误打误撞出这样一个答案：310341211012025105315

level 7：如果一个数位$i\in[0,9]$满足字符串中某两个$i$之间恰好隔了$i$个字符，那么$i$是好的。分数=好的数位的个数。

world 7

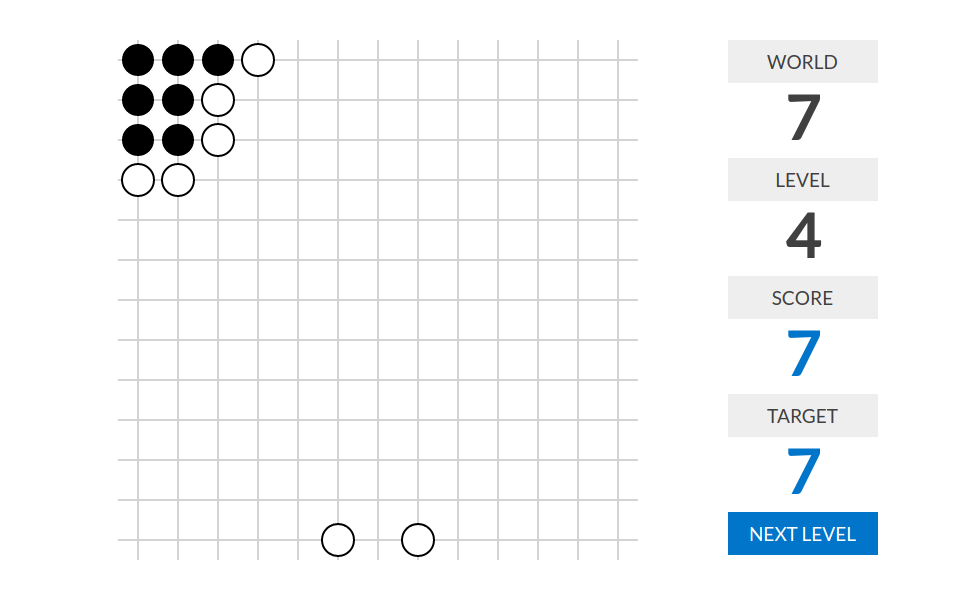
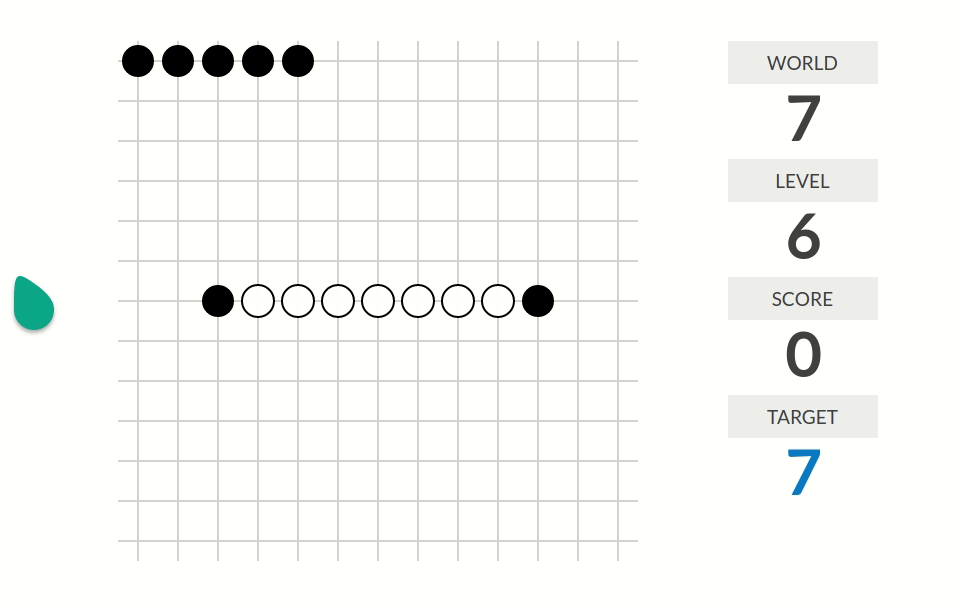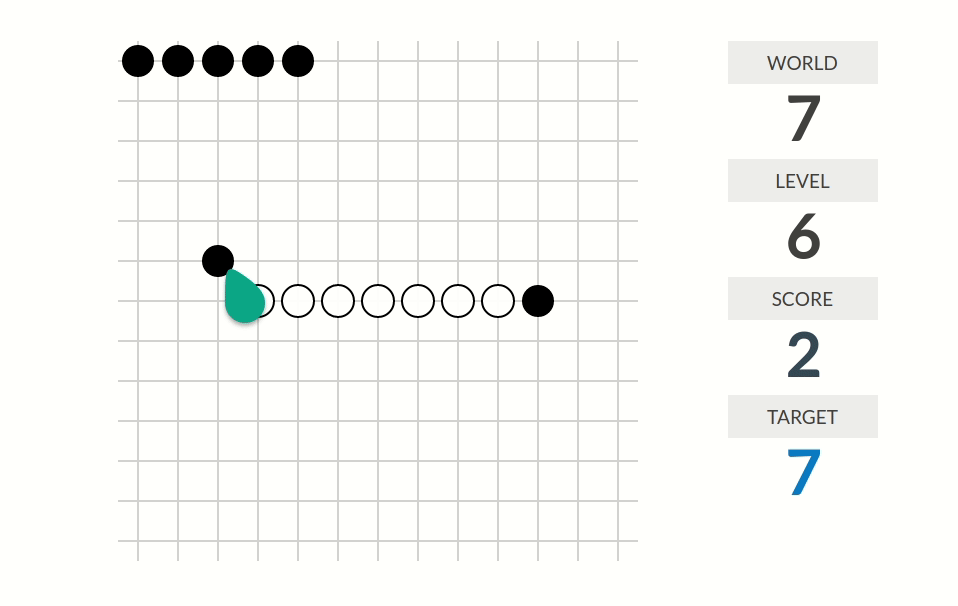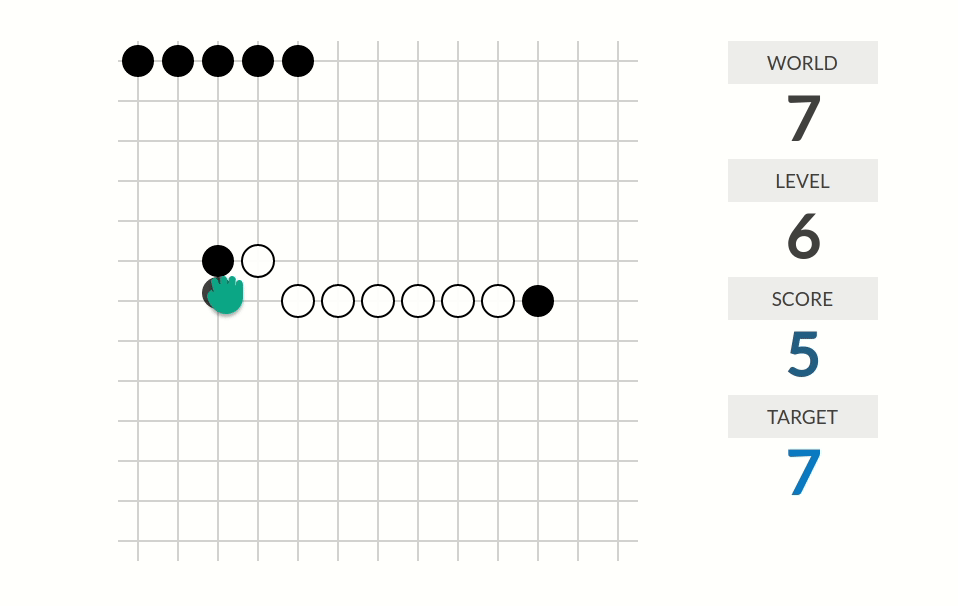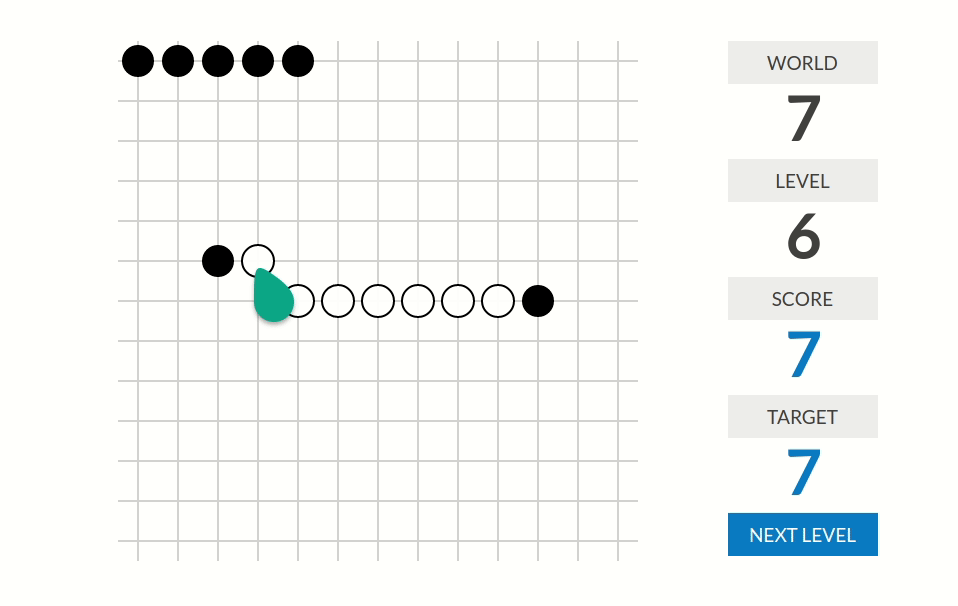
level 1：分数=不在那14个初始位置的棋子个数

level 2：分数=黑棋子 白棋子 相邻的pair的数量

level 3：分数=处于关于中心对称的位置的黑棋子和白棋子pair的数量

level 4：分数=没有气的黑棋个数。一个黑棋没有气当且仅当它到任意一个空格的四连通路径都需要经过某个白棋。

level 5：看上去只有在移动黑棋的时候会得到分数。分数是这样算的：从被移动的黑棋的位置（移动后的位置）出发沿着八个方向把八个方向的分数都加起来；如果沿着这个方向走是连续的$k$个白棋加一个黑棋那么这个方向的分数为$k$。

level 6：每连续移动两个不同颜色的棋子就加一分；每连续移动两个相同的棋子分数就归零。

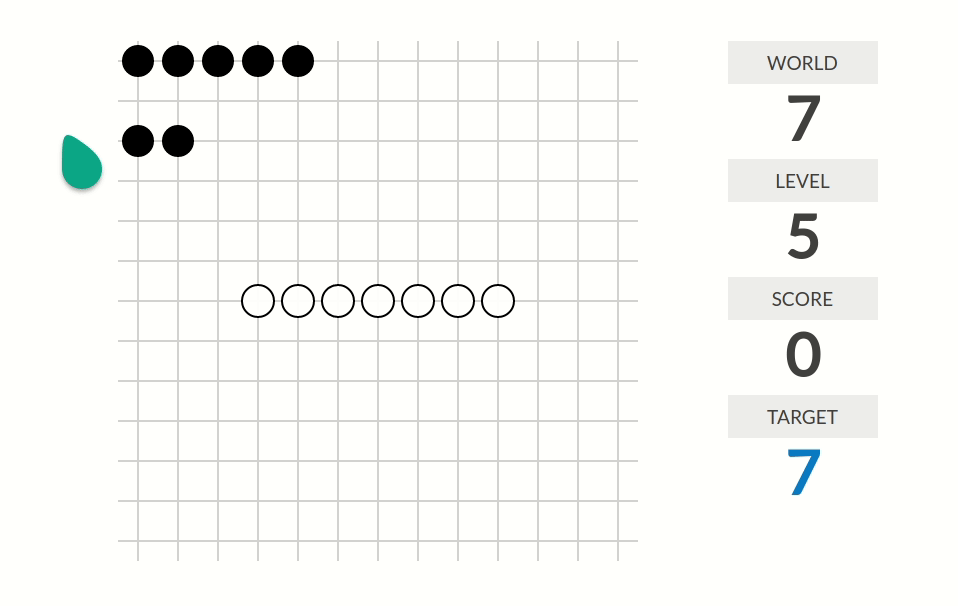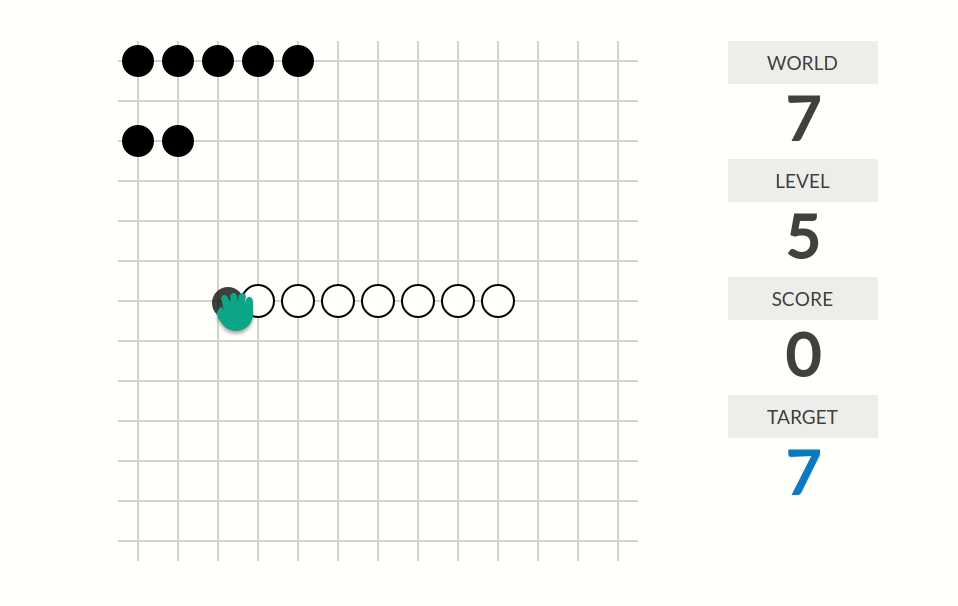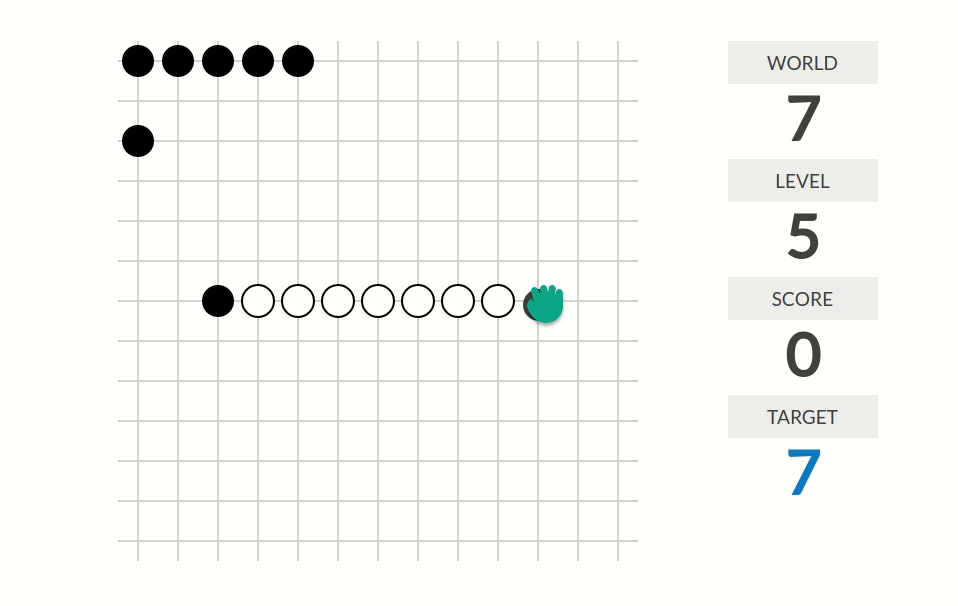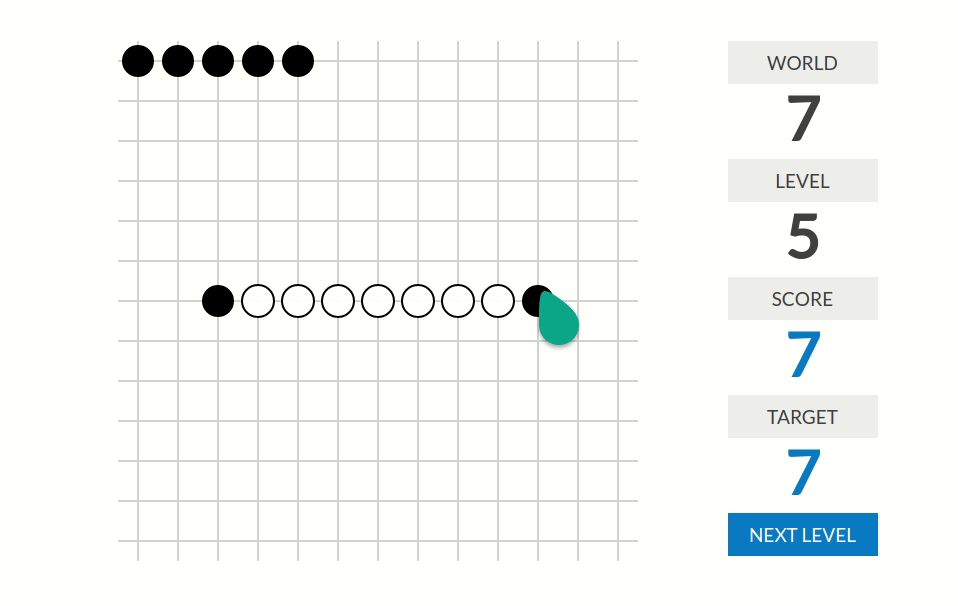
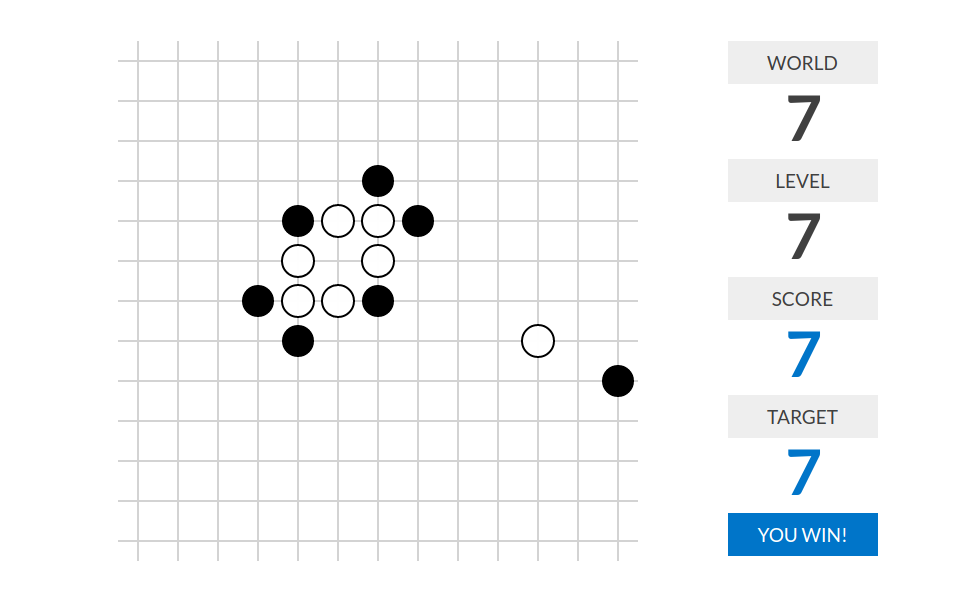
level 7：分数=好的直线个数。一条直线（斜率不限）是好的，当且仅当它上面恰好有两白两黑棋、且黑棋在两端、白棋在中间。