ITCS 2022 游记

ITCS 2022于今年1月31日至2月3日在线上举办。今年ITCS有很多很有趣的文章，我摘抄了几篇写了点笔记放出来。

Small Circuits Imply Efficient Arthur-Merlin Protocols

这篇文章研究的是一个经典问题：${\sf IP}$是否存在很小的${\sf AC}^0\circ {\sf XOR}$电路？这里，${\sf IP}(x, y) := \bigoplus_{i=1}^nx_iy_i$表示“Inner Product mod $2$”。

文章的主要结果是：假设${\sf IP}$可以被一个多项式大小的${\sf DNF}\circ{\sf XOR}$电路近似，那么${\sf IP}$有一个两轮、${\rm polylog}(n)$通信复杂度的Arthur-Merlin协议。于是，我们把一个电路复杂度的问题（${\sf IP}$的${\sf DNF}\circ{\sf XOR}$平均复杂度下界）规约到了一个通信复杂度的问题。

假设Alice知道$x$，Bob知道$y$，Merlin知道$x$和$y$，三方的计算能力都是无限的，但是Alice和Bob都不信任Merlin。现在我们需要在Merlin的帮助下，以尽可能少的通信计算${\sf IP}(x, y)$。我们分两步走：

• 第一步，我们先构造一个确定性的协议。给定$x, y$，这个协议只能证明${\sf IP}(x, y) = 1$（而不能证明${\sf IP}(x, y) = 0$）。并且，这个协议只能处理大部分$x, y$，对较少的$x, y$会出错。
  考虑一个中间层的${\sf AND}$门，管它叫做$g$。$g$底下是一些${\sf XOR}$门，设这些${\sf XOR}$门组成的线性空间的维度为${\rm dim}(g)$。如果${\rm dim}(g) \ge O(\log n)$，那么我们把$g$扔掉。注意到只有占比$2^{-{\rm dim}(g)}$的输入会满足$g$，所以当${\rm dim}(g)$太大的时候，我们扔掉$g$之后只会影响小部分输入。于是我们得到了一个被剪枝了的${\sf DNF}\circ{\sf XOR}$电路，它也能近似计算${\sf IP}$，且它的每个${\sf AND}$门的维度都只有$O(\log n)$。
  现在，我们要证明${\sf IP}(x, y) = 1$。Merlin找到这个电路中输出$1$的某个${\sf AND}$门，管它叫做$g$，然后把$g$的编号告诉Alice和Bob。于是Alice和Bob只需要计算${\rm dim}(g)$个${\sf XOR}$门的值——这只需要交换$O({\rm dim}(g))$个比特。
  这里重申一下该协议的两个缺点：（1）该协议只能证明${\sf IP}(x, y) = 1$，而不能证明${\sf IP}(x, y) = 0$。（2）对大部分的$x, y$，如果${\sf IP}(x, y) = 1$，那么该协议能够证明这一点；但是对于某些$x, y$该协议会失效——因为给出的电路是近似计算${\sf IP}$的，且我们砍掉了该电路中的一些${\sf AND}$门。
• 第二步，我们利用${\sf IP}$的性质来把这个协议变成一个完整的协议——对于所有的$x, y$，它可以用来证明${\sf IP}(x, y)$的值。最终完整的协议会使用随机数，且会有很小的概率出错。Alice和Bob分别选择随机串$u, v\in\{0, 1\}^n$，然后利用如下性质：
  \[{\sf IP}(x, y) = {\sf IP}(x \oplus u, y \oplus v) \oplus {\sf IP}(x\oplus u, v) \oplus {\sf IP}(u, y\oplus v) \oplus {\sf IP}(u, v).\quad(*)\]
  Alice和Bob随机选择$q = {\rm polylog}(n)$个不同的$u, v$给Merlin，然后要求Merlin给出上述式子中四个${\sf IP}$的值。Merlin还需要证明这$4q$个${\sf IP}$中尽可能多的等于$1$的${\sf IP}$确实等于$1$。然后，Alice和Bob相信Merlin没有证明的所有${\sf IP}$都等于$0$。这$4q$个${\sf IP}$的分布都是均匀随机的，所以就算上面那个协议会在某些$x, y$上出错，Merlin还是可以证明大部分等于$1$的那些${\sf IP}$。如果对于这$q$个实验中的大部分实验，$(*)$式中算出的${\sf IP}(x, y)$的值都相等，那么Alice和Bob认为这就是${\sf IP}(x, y)$的值。
  且慢，为什么Alice和Bob可以直接相信Merlin没有证明的${\sf IP}$都是$0$？这是因为在上述$4q$个${\sf IP}$中，等于$1$的${\sf IP}$大概率至少有$2q - O(\sqrt{q})$个，且Merlin可以证明这些${\sf IP}$中的绝大多数。（如果Merlin想要骗人，他不可能声明一个等于$0$的${\sf IP}$“等于$1$”，只能声明一个等于$1$的${\sf IP}$“等于$0$”。）那么Alice和Bob如果发现Merlin证明的${\sf IP}$（等于$1$）的个数太少了，就可以直接拒绝Merlin的证明。如果Merlin证明的${\sf IP}$等于$1$的个数足够多，那么Alice和Bob就可以相信剩下的${\sf IP}$都是$0$。

总结：如果${\sf IP}$可以被很小的${\sf DNF}\circ{\sf XOR}$电路近似，那么${\sf IP}$也有很好的Arthur-Merlin通信协议，这在通信复杂度中被认为是不太可能的。所以，我们把${\sf IP}$的电路复杂度下界问题规约到了一个通信复杂度问题。

Algorithms and Lower Bounds for Comparator Circuits from Shrinkage

这篇文章研究的是一种叫比较电路（comparator circuit）的计算模型。如下图就是一个比较电路：电路中有一些线（wire）和一些门（gate），每条线的初始值是某个$x_i$或$\lnot x_i$（可以有多条线有相同的初始值），每个门会输入两根线$a, b$，然后将$a$的新值赋成$a_{\rm new} := a\land b$，将$b$的新值赋成$b_{\rm new} := a\lor b$。

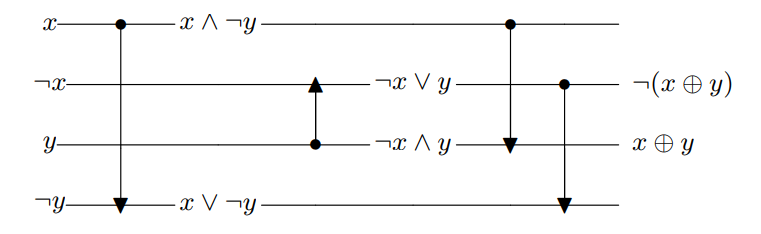
Gal和Robere证明了这种电路的第一个$\Omega((n/\log n)^{1.5})$的下界，这篇文章把上述结果推广到了平均复杂度下界、#SAT算法和PRG。

文章中最重要的技术是一个shrinkage引理：假设我们随机给若干变量赋值，那么我们会得到一个剩下的电路，这个电路作用在所有未赋值的变量上。shrinkage说的是：剩下的那个电路会比原电路显著更小。事实上，如果一个比较电路有$\ell$条线，那么它至多有$O(\ell^2)$个门（或者说与某个$O(\ell^2)$个门的电路等价）。所以如果我们随机将占比为$p$的变量赋值成$0$或$1$，那么期望意义下只会剩下$p\ell$条线，也就只剩下$O(p^2\ell^2)$个门了。

一个open problem：能否证明比$O(n^{1.5})$更强的比较电路的复杂度下界？我感觉有理由认为当前的技术不紧。。。。

Smaller ACC0 Circuits for Symmetric Functions

这篇文章证明了${\sf MAJ}$（事实上，任意对称函数）都可以用一个深度为$3$、大小为$2^{n^{o(1)}}$的${\sf CC}^0$电路计算。更精确地说，对任意$\epsilon > 0$，存在一个模数$m$，使得${\sf MAJ}$可以用一个深度为$3$、大小为$2^{n^\epsilon}$的只由${\sf MOD}_m$门构成的电路计算。作为对比，如果只允许用${\sf AND}$、${\sf OR}$和${\sf MOD}_2$，那么在深度为$3$的情况下我们至少需要$2^{\Omega(n^{1/2})}$大小的电路。这些结果表明${\sf ACC}^0$电路的表达能力很可能比我们想象中更加强大。

在这里我们只证明$\epsilon = 1/3 + o(1)$、$m = 30$的情况：事实上，存在一个计算${\sf MAJ}$的${\sf MOD}_5\circ {\sf MOD}_6\circ {\sf MOD}_5$电路，它的大小仅为$2^{O(n^{1/3}\log n)}$。

做法用的是中国剩余定理。首先考虑两个参数$T, s$，我们可以使用卢卡斯定理（见论文Theorem 3.2）构造一个度数不超过$O(2^s)$的多项式$p_2$，使得：

• 当$\sum_{i=1}^nx_i\equiv T\pmod {2^s}$时，$p_2(x_1, x_2, \dots, x_n) \equiv 0\pmod 2$，否则$p_2(x_1, x_2, \dots, x_n)\equiv 1\pmod 2$。

同理，给出参数$T, t$，我们可以构造一个度数不超过$O(3^t)$的多项式$p_3$，使得：

• 当$\sum_{i=1}^nx_i\equiv T\pmod {3^t}$时，$p_3(x_1, x_2, \dots, x_n) \equiv 0\pmod 3$，否则$p_3(x_1, x_2, \dots, x_n)\equiv 1\pmod 3$。

于是，如果我们取$2^s, 3^t\approx O(\sqrt{n})$，且$T\le n \le 2^s3^t$，那么我们就能够搞到一个度数为$O(\sqrt{n})$的多项式$p = 3p_2 + 2p_3$，使得$p\equiv 0\pmod 6$当且仅当$\sum_{i=1}^n x_i = T$。

有了这个多项式之后，我们就可以用一些分块小技巧了。我们把输入划分成$\ell = n^{1/3}$块，每块大小为$n^{2/3}$。我们枚举$\vec{T} = (T_1, T_2, \dots, T_\ell)$，其中$T_i$表示第$i$块中$1$的个数。对所有满足条件的$\vec{T}$，我们检查这个$\vec{T}$是否符合我们的输入。（如果我们算的函数是${\sf MAJ}$，那么“满足条件”的意思是$\sum_{i=1}^\ell T_i \ge n/2$；显然，这个做法也可以扩展到一般的对称函数上去。）一共有$2^{O(n^{1/3}\log n)}$种可能的$\vec{T}$。对一个固定的$\vec{T}$，我们只要用一个度数为$\sqrt{n/\ell}=O(n^{1/3})$的$\bmod 6$多项式就可以检查第$i$个块里是否恰好有$T_i$个$1$。我们把所有$\vec{T}$的检查结果用一个${\sf MOD}_5$合并起来就行了。（因为符合我们输入的$\vec{T}$要么有一个，要么一个也没有，所以最顶层可以选包括但不限于${\sf OR}$、${\sf MOD}_p$的门。）

这样，我们得到了一个计算${\sf MAJ}$的${\sf MOD}_5\circ {\sf AND}\circ {\sf MOD}_6\circ {\sf AND}$电路，它的大小是$2^{O(n^{1/3}\log n)}$，且每个${\sf AND}$的大小都是$O(n^{1/3})$。我们可以用一些经典的技术把${\sf AND}$门换成大小为$2^{O(n^{1/3})}$的${\sf MOD}_5$或${\sf MOD}_6$门，最终得到一个大小为$2^{O(n^{1/3}\log n)}$的${\sf MOD}_5\circ {\sf MOD}_6\circ {\sf MOD}_5$电路。

一个open problem：既然${\sf MAJ}$能用$2^{n^{o(1)}}$大小的${\sf CC}^0$电路计算，我们能不能用差不多大小的${\sf CC}^0$电路计算${\sf NC}^1$中的问题呢？（比如说$S_5$上的word problem？）

Pseudorandom Self-Reductions for NP-Complete Problems

这篇文章的结论很有意思！我先介绍一下背景。

如果一个问题$L$是${\sf NP}$-完全的，那么你无法把$L$的最坏情况规约到平均情况（除非${\sf NP}\subseteq{\sf coNP}_{/{\rm poly}}$）。比如说，你无法把“在最坏情况下解决$L$”规约到“在平均情况下解决$(L, {\cal U})$”，其中${\cal U}$是指$L$上的输入的均匀随机分布。HS17证明了如果存在单向函数（one-way functions），那么我们可以把“在最坏情况下解决${\sf GapMCSP}$”规约到“在平均情况下解决$({\sf MCSP}, {\cal U}')$”。这里${\cal U}'$是一个伪随机分布——任意多项式时间的算法无法区分${\cal U}$和${\cal U}'$。HS17把这一结论看成是${\sf MCSP}$和一般的${\sf NP}$-完全问题的一个不同点。

这篇文章证明了：假设Planted Clique是困难的，那么我们可以把“在最坏情况下解决${\sf Clique}$”规约到“在平均情况下解决$({\sf Clique}, {\cal U}')$”！其中${\sf Clique}$是最大团问题（这是个${\sf NP}$-完全问题！），${\cal U}'$是一个伪随机分布。这说明HS17的结论不应该看成“${\sf MCSP}$和一般的${\sf NP}$-完全问题的不同点”，而是应该看成“伪随机规约比真随机规约更强”。

具体地说，文章中的规约长这样：首先我们假设我们只需要区分最大团大小$\le n^{0.1}$和最大团大小$\ge n^{0.9}$。（这是因为$n^{0.8}$-近似最大团仍然是${\sf NP}$-完全的。）给出一个图$G$，令$f(G)$为如下的随机图：随机取一个大小为$n^{0.3}$的集合$S$，然后$f(G)$中$S$内部的边与$G$完全相同，剩下的边完全随机。

• 正确性：如果$G$的最大团大小$\ge n^{0.9}$，那么$f(G)$的最大团大小大概率至少是$n^{0.2}$。如果$G$的最大团大小$\le n^{0.1}$，那么$f(G)$的最大团大小大概率也不会超过$n^{0.1}$。
• 伪随机性：如果令$K_S$表示$S$上的完全图，$\oplus$表示异或操作，那么$f(G)\oplus G\oplus K_S$的分布恰好是一个偷偷插入了一个大小为$n^{0.3}$的团的随机图。如果Planted Clique假设成立，那么$f(G)\oplus G\oplus K_S$是伪随机的，所以$f(G)$也是伪随机的。

Excluding PH Pessiland

文章的结果是：${\sf DistPH}$的复杂度很高，当且仅当存在一个可以在${\sf PH}$内计算出来的PRG。“复杂度很高”有两种定义方法——${\sf BPP}$算法无法解决某个问题、或者${\sf P}_{/{\rm poly}}$算法无法解决某个问题。对于这两个定义，文章都证明了上述等价性。

• ${\sf DistPH}\not\subseteq {\sf HeurP}_{/{\rm poly}}$当且仅当${\sf PH}$内可以计算出${\sf P}_{/{\rm poly}}$无法破解的PRG。
  $\implies$方向：用Yao's XOR lemma和Nisan-Wigderson PRG。
  $\impliedby$方向：可以用Liu-Pass来证明${\rm MINK}^{{\rm poly}, {\sf PH}}$在均匀随机的输入上是困难的。
• ${\sf DistPH}\not\subseteq {\sf HeurBPP}$当且仅当${\sf PH}$内可以计算出${\sf BPP}$无法破解的PRG。
  $\implies$方向：由于Nisan-Wigderson PRG只能搞${\sf P}_{/{\rm poly}}$不能搞${\sf BPP}$，所以我们得用其他的PRG。这里我们使用advice complexity很小的direct product PRG（$\rm DP$）。如果$\rm DP$不安全，那么${\sf DistPH}\subseteq{\sf HeurBPP}_{//\log}$。然后我们用一些其他的思路把这$\log n$位的advice去掉（具体没太看）。
  $\impliedby$方向：破解一个${\sf PH}$内计算出来的PRG可以规约到一个平均复杂度问题$(L, {\cal D})$，其中$L\in{\sf PH}$，${\cal D}$是一个能用${\sf PH}$的复杂度采样的输入分布。因为${\sf DistPH}\subseteq {\sf HeurBPP}$，我们可以用一个多项式时间采样的分布${\cal D}'$来近似${\cal D}$。再用一遍${\sf DistPH}\subseteq {\sf HeurBPP}$，我们有$(L, {\cal D}')\in{\sf HeurBPP}$，于是这个PRG是不安全的。

不管是哪种情况，本文都证明了一个很有趣的结论：$({\rm MINK}^{{\rm poly}, {\sf PH}}[n - \log n], {\cal U})$是${\sf DistPH}$中最难的问题，其中${\cal U}$是均匀随机分布。

这篇文章可以和Hirahara-FOCS20对比着阅读！虽然技术不太一样，但是它们的结论很相似：

• 这篇文章：${\sf DistPH}\subseteq {\sf HeurBPP}$当且仅当${\rm MINKT}^{\sf PH}\times\{{\cal U}\}\in{\sf HeurBPP}$当且仅当${\sf PH}$中没有无法被${\sf BPP}$破解的PRG。
• Hirahara-FOCS20：${\sf DistPH}\subseteq {\sf AvgP}$当且仅当${\rm GapMINKT}^{\sf PH}\in{\sf P}$当且仅当${\sf PH}$中没有无法被${\sf P}$破解的HSG。（最后一个“当且仅当”需要假设${\sf P} = {\sf ZPP}$。）

另外我看了一下这篇文章的视频，Shuichi提出了“${\sf PH}$版本的五个世界”，感觉很有意思！

Improved Merlin-Arthur Protocols for Central Problems in Fine-Grained Complexity

视频里讲了3SUM的Merlin-Arthur协议，我好像听懂了所以就摘抄一下（

给出整数$t$和$a_1, a_2, \dots, a_n$，我们希望在$\tilde{O}(n)$的时间内证明不存在$i, j, k$使得$a_i + a_j + a_k = t$。首先，Merlin选择一个比较好的质数$p\le n^2$，使得满足$a_i + a_j + a_k \equiv t \pmod p$的$(i, j, k)$的个数不超过$\tilde{O}(n)$。（因为每个$(i, j, k)$只会给$O(\log n)$个质数做贡献，所以这样的$p$是存在的。）接下来，Merlin把所有满足$a_i + a_j + a_k \equiv t \pmod p$的$(i, j, k)$都发给Arthur。最后，Merlin还需要向Arthur证明他已经发了所有可能的$(i, j, k)$。于是我们把问题归结到了如下版本的#3SUM：

由于只有三个数相加，所以三个数的和一定是$t$、$t+p$或者$t+2p$。简单起见我们只考虑证明$a_i+a_j+a_k=t$的解有$count$个的情况。

注意这个版本的问题与最一般的3SUM问题的区别在于：所有的$a_i$都不超过$n^2$了。接下来我们用某种“分块”把$a_i$的值域分成$O(n)\times O(n)$，然后使用一些FFT的技术。具体地说，令$A(x) = \sum_{i=1}^n x^{a_i}$，$A(x)^3 = \sum_{t=1}^{3n^2} b_tx^t$，那么$b_t$就是满足$a_i+a_j+a_k=t$的$(i, j, k)$的个数。我们搞一个如下的分块trick：令$T = \{t' \le 3n^2: t' \equiv t \pmod n\}$，可以把$T$看成一个步长为$n$的包含$t$的等差数列。我们把$A(x)^3$的次数在$T$内的那些项都拿出来，得到多项式
\[\bar{A}(r) = \sum_{s\in T}b_sr^s.\]
Merlin会给Arthur发送$\bar{A}$的所有系数（于是当然也会发送$b_t$）。设Merlin发送的系数为$\bar{A}_{\rm Merlin}(r) = \sum_{s \in T}{\rm merlin}_sr^s$。Arthur只需要随机选取一个数$r$并计算$\sum_{s\in T}{\rm merlin}_sr^s$，并验证其的确等于$\bar{A}(r)$即可。

现在问题变成我们需要在$\tilde{O}(n)$的时间内计算$\bar{A}(r)$。事实上，$\bar{A}(r)$就是多项式$A(xr)^3\bmod (x^n-1)$在第$x^{t\bmod n}$项的系数。我们只要先算出多项式$A(xr)\bmod (x^n-1)$然后再求立方即可，这可以用FFT在$\tilde{O}(n)$的时间内完成。

Average-case Hardness of NP and PH from Worst-case Fine-grained Assumptions

为了解释这篇文章在干嘛，我们需要先回顾一下它的前作（Hirahara-STOC21）。前作证明了如果${\sf DistNP}\subseteq{\sf AvgP}$，那么${\sf UP}\subseteq{\sf DTIME}[2^{O(n/\log n)}]$。

具体地说，定义一个串的计算深度（computational depth）为${\rm cd}^{s, t}(x) = {\rm K}^s(x) - {\rm K}^t(x)$，其中$s,t$为两个参数。假设${\sf DistNP}\subseteq{\sf AvgP}$，那么存在一个多项式$p$使得如下结论成立：对任意$L\in{\sf UP}$，存在一个（最坏复杂度下的）算法，给出输入$x$和参数$t$，令$k = {\rm cd}^{t, p(t)}(x)$，能在${\rm poly}(n, t, 2^k)$时间内算出$L(x)$。于是，我们有如下的trick：令$I = \epsilon \log n$为一个参数，$t_0$为一个初始值，$t_i = p(t_{i-1})$。我们有

\[n\ge {\rm K}^{t_I}(x) - {\rm K}^{t_0}(x) = \sum_{i=1}^I{\rm cd}^{t_{i-1}, t_i}(x),\]

所以一定存在一个$i$使得${\rm cd}^{t_{i-1}, t_i}(x) \le n/I$。这样的话，我们就可以在${\rm poly}(n, t_I, 2^{n/I}) \le 2^{O(n/\log n)}$的时间内解决$L$。

这篇文章证明了一个更加精细的结论：如果${\sf DistNTIME}[n]\subseteq {\sf AvgTIME}[\tilde{O}(n)]$，那么${\sf UP}\subseteq {\sf DTIME}[2^{O(\sqrt{n\log n})}]$。我觉得这篇文章最重要的insight是：如果上述推导中的$p$不仅仅是个多项式，而且是$\tilde{O}(n)$的，那么在精心选取$I$之后，最终的复杂度会变成$2^{O(\sqrt{n\log n})}$。当然，文章需要用很多新的技术才能把$p$从多项式改进到$\tilde{O}(n)$。

Beating Classical Impossibility of Position Verification

虽然是我完全不懂的领域但是我听了talk之后觉得问题很有意思！于是我稍微记录一下（

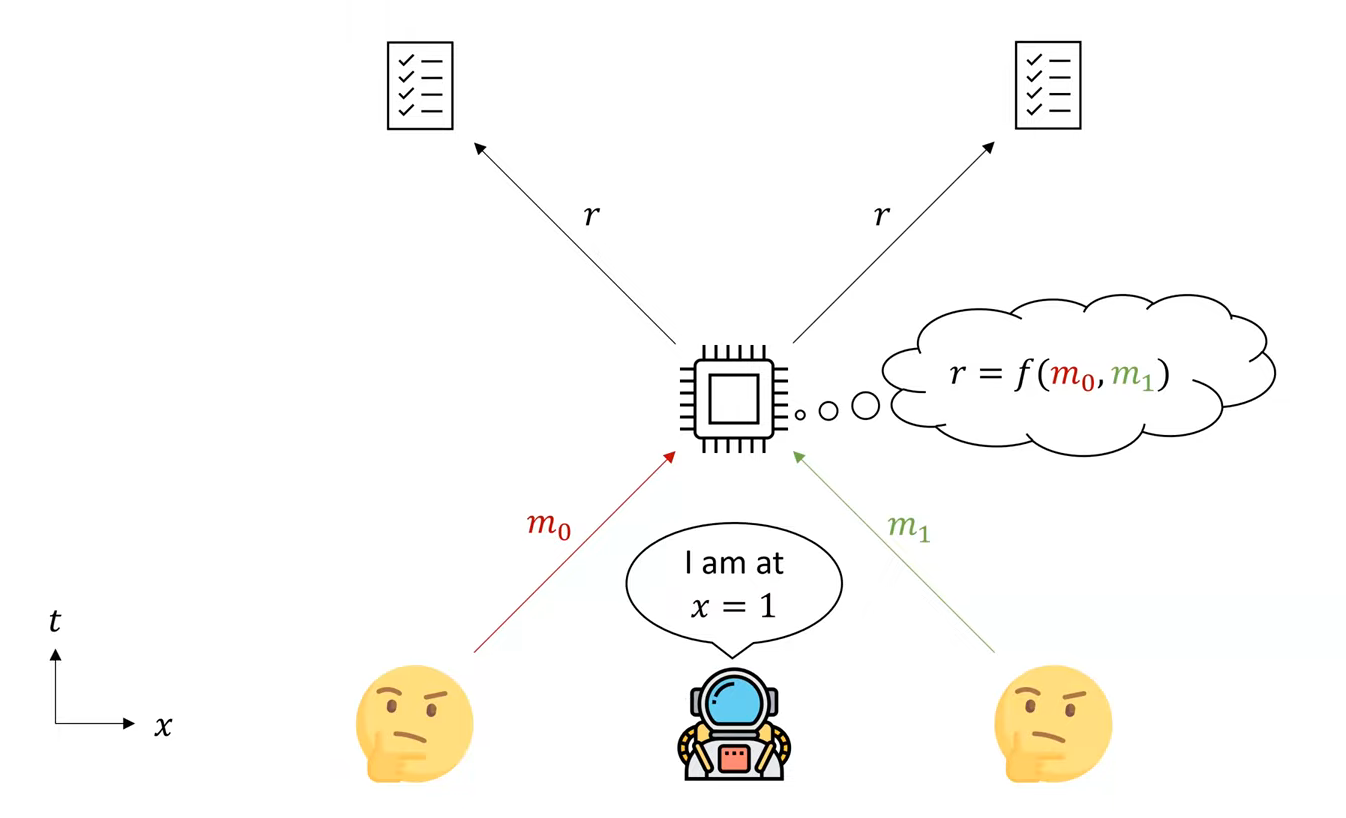
问题是这样的：假设有一个宇航员（称他为prover好了），他希望向我们证明他所在的位置。我们可以和他互相发信息，并且假设信息的传播速度等于光速。prover可以向我们证明他的位置吗？简单起见假设空间是一维的，光速等于$1$，我们在坐标$0$和$2$处有两个verifier（分别称作$V_0$和$V_2$），prover希望证明他的坐标是$1$。如果prover是恶意的（即：坐标不是$1$但是希望骗过verifier），那么他可以控制$1$除外的所有位置。（比如说可以有两个prover，一个在$0.5$，一个在$1.5$。）

一个naïve的做法如下：事先确定一个函数$f$。两个verifier分别向prover发送信息$m_0, m_1$，然后prover在收到所有信息后立即把$f(m_0, m_1)$返回给两个verifier。如果两个verifier都能在两个单位时间内收到正确的答案，那么我们认为prover的确是在坐标$1$的。可以参考下图，其中横轴是空间、纵轴是时间。

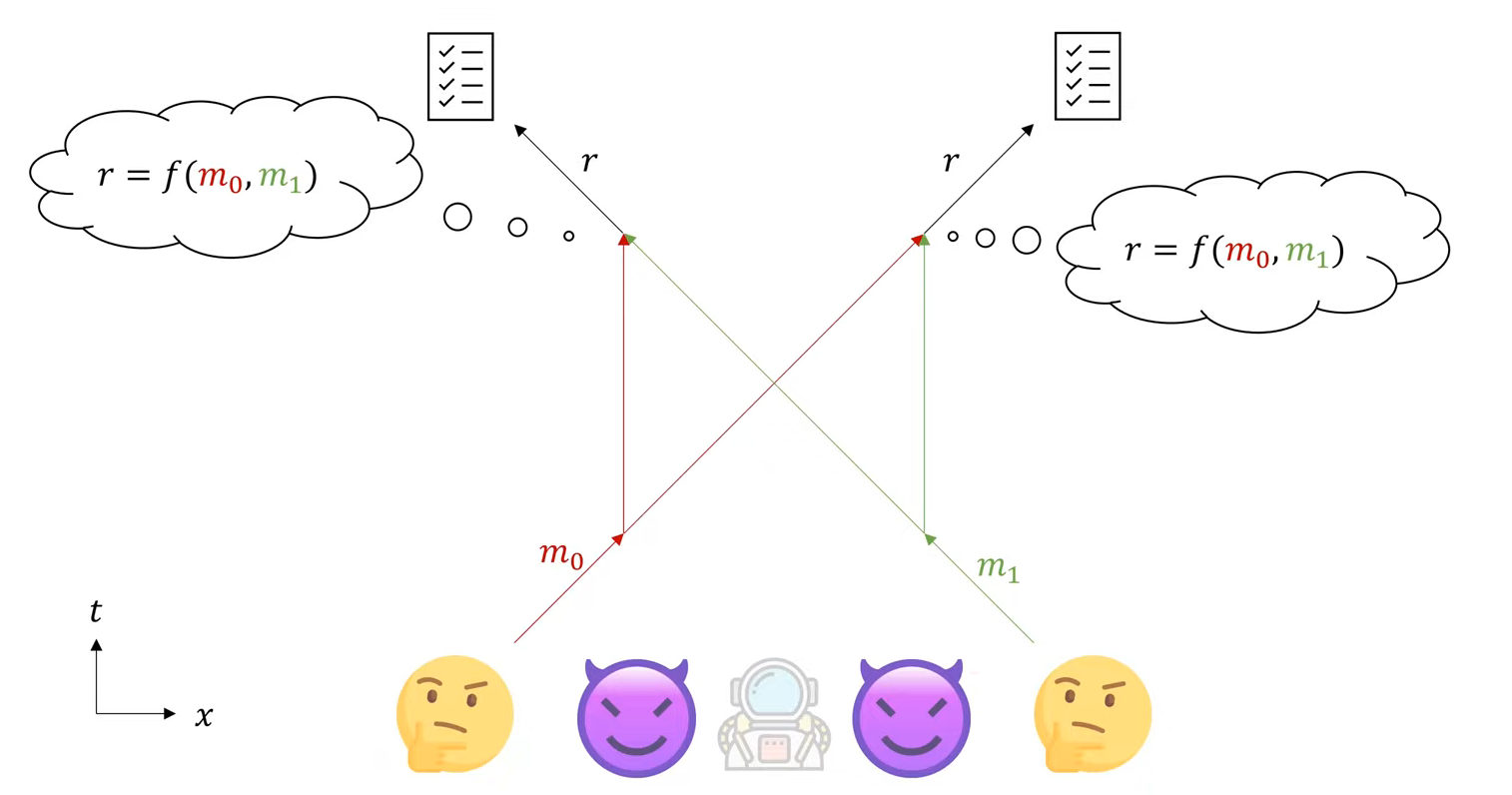
这个naïve的做法是不安全的！假设空间中有两个（恶意的）prover $A_0$、$A_1$，其中$A_0$在$r$处、$A_1$在$2-r$处。那么$A_0$可以在收到$m_0$后立马把$m_0$传给$A_1$，$A_1$在收到$m_1$后立马把$m_1$传给$A_0$，$A_0$在收到$m_1$后把$f(m_0, m_1)$传给$V_0$，$A_1$在收到$m_0$后把$f(m_0, m_1)$传给$V_2$。这样，虽然$A_0$和$A_1$都可以离$x=1$很远，但是他们可以联合起来骗过两个verifier。如下图。

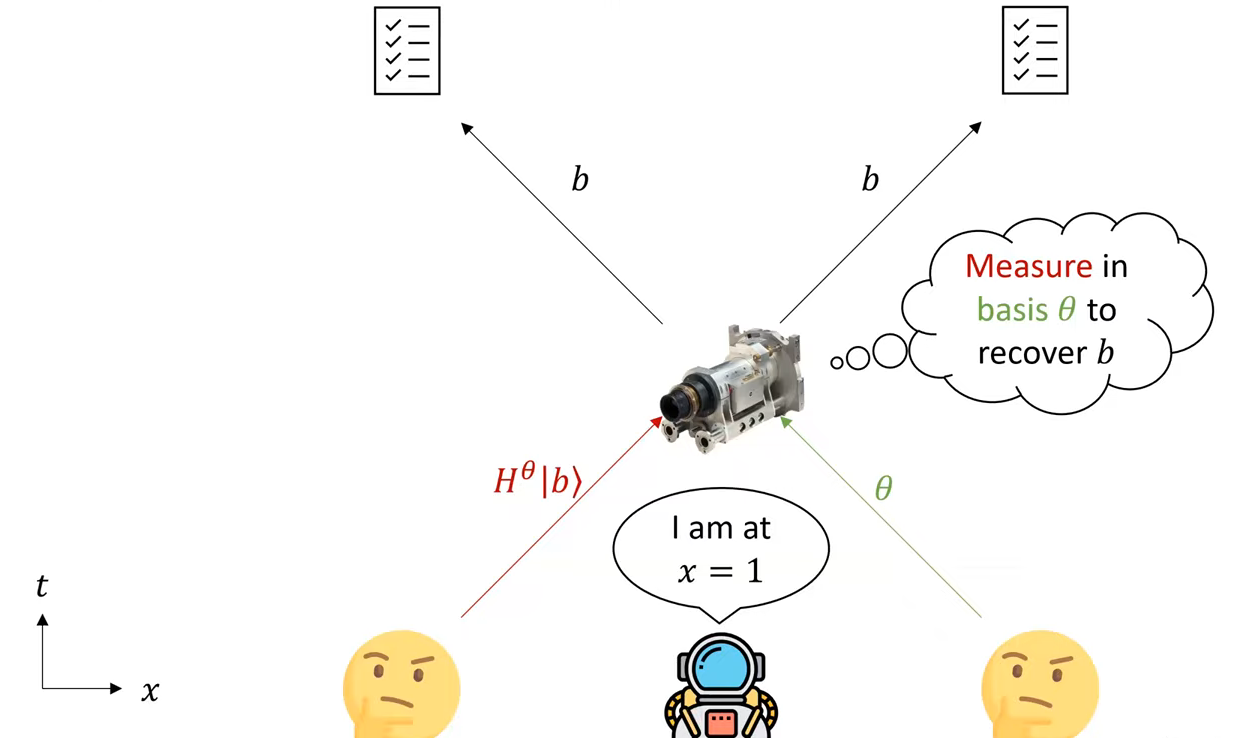
如果只考虑经典的prover和verifier的话，这件事情其实是不可能的！于是我们考虑量子协议。注意到上述攻击中，$A_0$需要把消息$m_0$复制一遍然后传给$A_1$，而量子信息是不可复制的。利用这一点，我们可以构造一个量子协议：$V_0$给prover发送一个BB84量子态（形如$H^\theta|b\rangle$，其中$\theta,b\in\{0, 1\}$，$H$是Hadamard变换），同时$V_2$给prover发送$\theta$。prover在得到了量子态和$\theta$之后，根据$\theta$决定如何观测得到的量子态（$\theta=0$就是标准基、$\theta=1$就是Hadamard基），然后将观测结果发送给两个verifier即可。注意，如果有两个恶意的prover $A_0$、$A_1$的话，$A_0$会需要把量子态复制一份发给$A_1$，而根据不可复制定理，这件事是做不了的。

注意到上述协议要求verifier向prover发送一些量子信息。本文考虑的是如下问题：一个经典的verifier能不能验证prover的位置？（也就是说verifier的计算能力是经典的、同时只能给prover发送经典信息。）本文证明了这样的协议至少蕴含一个proof of quantumness——也就是说prover不仅得是量子的，还得能够向verifier证明他有做量子计算的能力！另一方面，基于之前的一个proof of quantumness的协议，本文提出了一个只需要经典verifier的位置验证协议。（协议的安全性是基于LWE的量子复杂性的。）此外，文章中使用了一种叫“computational no-cloning”的概念：多项式时间的量子计算机无法克隆某些量子态。

Secret Sharing, Slice Formulas, and Monotone Real Circuits

设$f:\{0, 1\}^n \to \{0, 1\}$是一个单调函数，本文研究了$f$的三种复杂度：

• Secret sharing：假设我们有一个秘密要发给$n$个人，我们给每个人发一些消息，并且使得如下条件成立。对任意$x\in\{0, 1\}^n$，假设$x_i = 1$的这些人聚在一起共享他们得到的消息。那么当且仅当在$f(x) = 1$时，他们能够还原出我们发送的秘密。$f$的秘密共享复杂度即为至少需要给大家发送的消息总长度。
• Formula over slices：一个$(k,\ell)$-slice门是指任意一个$\ell$个输入的函数$g$，使得$g$接受所有$1$的个数大于$k$的输入，并拒绝所有$1$的个数小于$k$的输入。在$1$的个数等于$k$的输入上，$g$可以是任意函数。$f$的FOS复杂度即为用slice门组成的formula计算$f$所需要的最少的slice门的个数。
• monotone real formula：我们希望用一个formula来计算$f$，其中这个formula的每个门都计算一个单调的实值函数$f:\mathbb{R}\times\mathbb{R}\to\mathbb{R}$。（因此每条线储存的是一个实数。）当然，formula的输入输出必须都是$0$和$1$。$f$的MRF复杂度即为计算$f$的formula所需要的最少的门的个数。

一般的计算模型中，一个随机的$n$个变量的函数大约需要$2^n$的复杂度才能计算。但是对于这三个模型，任何单调函数都有$(1.5+o(1))^n$的复杂度上界！Applebaum和Nir构造了一个$(1.5+o(1))^n$复杂度的秘密共享机制；本文发现这个构造可以转化为$(1.5+o(1))^n$复杂度的FOS和MRC。

本文证明了单调${\sf NP}$中存在一个FOS复杂度和MRF复杂度都至少是$2^{\Omega(n/\log^2 n)}$的函数。所以，如果我们希望通过改进FOS和MRF的复杂度上界来证明秘密共享复杂度上界，那么这一做法不可能比$2^{O(n/\log^2 n)}$更优。

PCPs and Instance Compression from a Cryptographic Lens

因为我太懒了所以只讲PCP，不讲instance compression。考虑一个${\sf NP}$中的问题$L$，假设它的输入长度比witness长度要大很多。（例如：$L$的输入是一个大小为$n^{\omega(1)}$的电路，witness是它的一个SAT assignment。注意这里的witness长度只有$n$。）我们希望构造一个常数询问的PCP，且PCP证明的长度只和witness长度有关，和输入长度无关。（在上面那个例子中，我们希望PCP证明的长度为${\rm poly}(n)$。）Fortnow和Santhanam证明了除非${\sf NP}\subseteq{\sf coNP}_{/{\rm poly}}$，否则这样的PCP是不存在的。

但是，我们可以这样放宽PCP的要求：原来的PCP要求$x\not\in L$时不存在任何合法的证明；现在我们只需要$x\not\in L$时，任意多项式时间的malicious prover都无法生成一个合法的证明。在一些密码学的假设下，这样的PCA（“probabilistic checkable argument”）是存在的！本文的主要贡献是：基于LWE构造了一个各种参数更优的PCA。本文主要用到的技术是JKKZ的SNARG for ${\sf P}$。

视频中提到了一个很有意思的问题。众所周知，PCP和近似问题的复杂度（hardness of approximation）有关。我们能否利用文章中构造出来的PCA证明一些（目前无法被PCP证明出来的）近似问题的复杂度下界？