FOCS 2021 笔记

因为我没有注册FOCS 2021所以这篇博客不叫“游记”！我打算这几天把FOCS 2021的视频过一遍，整理一些我觉得不错的文章发在博客上。（立flag

Unambiguous DNFs and Alon-Saks-Seymour

视频讲得很深入浅出，是我看过的最有创意的talk之一，强烈推荐去观看！

这篇文章构造了一个函数$f:\{0, 1\}^{n^2} \to \{0, 1, \star\}$，使得：

• $C_0(f), C_1(f) = O(n)$：对任意输入$x$，如果$f(x) = 0$或$f(x) = 1$，那么只需要揭露$x$的$O(n)$位就可以证明$f(x)$的值。
• $C_{\bar{0}}(f), C_{\bar{1}}(f) = \Omega(n^{1.5})$：存在一个输入$x$，使得$f(x) = \star$，且需要揭露$x$的$\Omega(n^{1.5})$位才能够证明$f(x)\ne 0$（或者证明$f(x) \ne 1$）。

这个函数做到了$C_0, C_1$与$C_{\bar{0}}, C_{\bar{1}}$的$n$ vs $n^{1.5}$的分隔。这篇文章（的最终版本）将其改进到了平方级。同时，利用这个构造，这篇文章解决了许多其他的问题，包括：

• Alon-Saks-Seymour问题：存在一族图$G$，使得$\chi(G) \ge \exp(\Omega(\log^2 {\rm bp}(G)))$。这里，$\chi(G)$是$G$的色数；${\rm bp}(G)$表示$G$的biclique partition number，即$G$能够写成至少多少个完全二分图的不交并。
• unambiguous DNF问题：存在一族宽度为$k$的unambiguous DNF（每个答案为$1$的输入只满足恰好一个子句），使得它写成CNF后宽度至少是$\tilde{\Omega}(k^2)$。

Hardness vs Randomness, Revised: Uniform, Non-Black-Box, and Instance-Wise

我操，这paper太牛逼了，妈的（但是我目前还不会

在这里瞎编几个future direction吧：

• Chen-Tell STOC21和Chen-Tell FOCS21用的假设都不是很完美的样子——例如STOC21那篇文章需要用一个OWF；FOCS21那篇文章需要bounded-depth且只能构造一个targeted HSG（而不是PRG）。能不能把这些假设去掉？
• 这几篇Chen-Tell反复提到了superfast derandomization。（对于一个不相信NSETH的人来说）到底能不能证明${\sf BPTIME}[T(n)]\subseteq {\sf DTIME}[n^{0.99}\cdot T(n)]$呢？或者一个简单一点的问题：${\sf UPIT}$能不能在确定性$n^{1.99}$时间内解决？

Constructive Separations and Their Consequences

我很喜欢这篇文章传达出的big picture：（1）现有的很多复杂度下界并不是constructive的，而且把它们改进成constructive的会需要证明一些breakthrough（例如${\sf P}\ne {\sf NP}$）；（2）很多breakthrough（例如${\sf P}\ne {\sf NP}$）的证明一定是constructive的。所以，constructivity似乎是我们会希望复杂度下界所拥有的某种性质？

当然，我其实怀疑这样的big picture到底多大程度上是对的（第2条是定理所以肯定是对的，但是第1条存疑）。例如停机问题不可解的证明其实就是constructive的：给出一个图灵机$M$的代码，我们可以很轻松地构造出停机问题的一个实例，使得$M$在这个实例上出错。视频中说对角线法证明的下界一般都是constructive的；更加“组合”的方法证明的下界一般不是constructive的。

可以认为对角线法是“第一代复杂度下界”（从time hierarchy到relativization），组合方法是“第二代复杂度下界”（从switching lemma到natural proofs）。我们现在将对角线法与组合方法结合，证出了很多“第三代复杂度下界”——典型的例子如${\sf MA}_{/1}\not\subseteq{\sf SIZE}[n^k]$和${\sf NEXP}\not\subseteq{\sf ACC}^0$。这些下界是constructive的吗？

Quantum learning algorithms imply circuit lower bounds

OS17证明了经典的学习算法能够推出${\sf BPEXP}$的复杂度下界，这篇文章证明了量子学习算法能够推出${\sf BQEXP}$的复杂度下界。证明思路如下：

• 首先，给出一个非平凡的量子学习算法，我们可以搞出一个量子Natural Proof（可以看成是${\sf MCSP}$的量子heuristic）。
• 接下来我们使用一个win-win argument。如果${\sf PSPACE}\subseteq {\sf BQSubEXP}$，那么我们能直接由${\sf SPACE}[n^{\omega(1)}]\not\subseteq{\sf P}_{\rm /poly}$推出${\sf BQEXP}\not\subseteq{\sf P}_{\rm /poly}$。
• 如果${\sf PSPACE}\not\subseteq{\sf BQSubEXP}$，那么我们需要构造一个能够 fool 量子算法的PRG。这个构造是本文的重点。在构造完了该PRG之后，我们用它来 fool 我们的量子Natural Proof，就能找到一个hard function了。

IW98证明了如果${\sf PSPACE}\not\subseteq{\sf B{\color{red}P}SubEXP}$，那么我们可以构造一个 fool 经典随机算法的PRG。这篇文章的重点是把这个构造推广到量子的情形。我们需要使用的技术有：一个好的${\sf PSPACE}$-完全问题（TV07，现成的）、hardness amplification（IJKW + Goldreich-Levin，需要推广到量子情形）、Nisan-Wigderson PRG（需要推广到量子情形）。

Winning the War by (Strategically) Losing Battles: Settling the Complexity of Grundy-Values in Undirected Geography

注：这里假设读者了解基本的组合博弈论（比如Sprague-Grundy定理）、以及了解有向/无向图上的地理游戏的定义。有向图上的地理游戏是${\sf PSPACE}$-完全的；无向图上的地理游戏可以用一般图最大匹配解决，所以是多项式时间内的。

这篇paper证明了如下结论：计算无向地理游戏的Grundy值是${\sf PSPACE}$-完全的！视频中给出了一个将有向地理游戏规约到同时玩两个无向地理游戏的方法。第一个无向地理游戏是由有向地理游戏的输入改编来的，第二个无向地理游戏很简单，只有一条边：

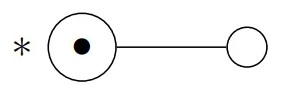
同时玩两个游戏的意思是：轮到某方操作时，他可以选择两个游戏中的某一个，然后进行一步操作；不能操作者输。后手必胜当且仅当这两个游戏的Grundy值相等（换句话说，它们的nim-sum——也就是异或——等于$0$）。第二个游戏只能操作一步，所以其Grundy值为$1$。所以这篇文章实际上证明了一个更强的推论——判定无向地理游戏的Grundy值是否为$1$就已经是${\sf PSPACE}$-完全的了！

规约很简单，我们把有向图的每条边$(x\to y)$换成一个gadget，使得这个gadget中只能从$x$走到$y$，不能从$y$走到$x$。具体的gadget长这样：

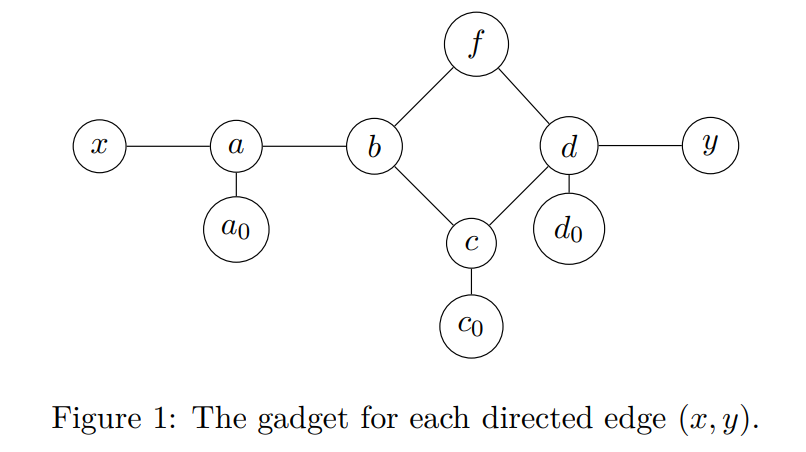
我们可以从$x$走到$y$。假设Alice在$x$处，那么她只能从$x$走到$a$。如果Bob接下来从$a$走到$a_0$的话，那么Alice走一下第二个游戏（只有一条边的那个）就能赢了，所以Bob接下来一定要从$a$走到$b$。然后，Alice可以从$b$走到$c$。同理Bob不可以从$c$走到$c_0$（否则他就输了），于是他只能走到$d$。接下来Alice再从$d$走到$y$即可。

我们不能从$y$走到$x$（于是这个gadget实现了一条有向边）！假设Alice在$y$处，那么她只能从$y$走到$d$。Bob可以选择从$d$走到$f$，然后Alice唯一的选择就是从$f$走到$b$。此时Bob再从$b$走到$c$，于是Alice唯一的选择就是走到$c_0$。Bob再动一下第二个游戏就赢了。

Amortized Circuit Complexity, Formal Complexity Measures, and Catalytic Algorithms

这篇文章很有意思，而且是我不太熟悉的领域，所以我打算多写点，试图把它的故事给讲清楚。

均摊复杂度：设$f$是一个函数，$C$是某种复杂度（例如$C(f)$是计算$f$所需要的电路大小）。如果我想计算如下函数$f^m$：

\[f^m(x_1, x_2, \dots, x_m) = (f(x_1), f(x_2), \dots, f(x_m)),\]

我是否能够做到比$m\cdot C(f)$更优的复杂度？我们定义$f$的均摊复杂度为：

\[\tilde{C}(f) := \lim_{m\to\infty}\frac{C(f^m)}{m}.\]

如果$\tilde{C}(f) < C(f)$，那么一定存在某个$m$，使得我们在计算$f^m$时，有比“暴力计算$m$个$f$”更高效的做法。那么对于哪些$C$、哪些$f$，我们有$\tilde{C}(f) < C(f)$？

形式化复杂度量：在研究公式（formula）复杂度时，人们引入了如下概念。假设$\mu$是一个将所有布尔函数映到$\mathbb{R}_{\ge 0}$的函数，且满足：

• 对所有单变量函数$f$（$f=x_i$或者$f=\lnot x_i$），$\mu(f) \le 1$；
• 对所有函数$f,g$，$\mu(f\land g) \le \mu(f) + \mu(g)$；
• 对所有函数$f,g$，$\mu(f\lor g) \le \mu(f) + \mu(g)$。

那么我们管$\mu$叫做一个形式化复杂度量（formal complexity measure）。不难看出，记${\rm L}(f)$为$f$的公式复杂度，那么${\rm L}$是一个形式化复杂度量，且对任意$f$，${\rm L}(f)$是所有合法的形式化复杂度量$\mu$中，$\mu(f)$最大的那个。历史上，${\sf PARITY}$需要$n^2$大小的公式就是用这种方法证明的：Krapchenko构造了一个形式化复杂度量（可以参阅Ingo Wegener的教材 Sec 8.8），且该度量在${\sf PARITY}$上的值等于$n^2$，于是我们有${\rm L}(f) \ge n^2$。

我们也可以把形式化复杂度量推广到其他的计算模型上，每一种计算模型对应着一种复杂度量。例如，对于比较器电路（comparator circuits）模型，它对应的形式化复杂度量是这样定义的：

• 对所有单变量函数$f$，$\mu(f)\le 1$；
• 对所有函数$f,g$，$\mu(f\lor g) + \mu(f\land g) \le \mu(f) + \mu(g)$。

满足以上两条性质的形式化复杂度量称作次模复杂度量（submodular complexity measure）。注意：令${\rm C}(f)$为$f$的比较器电路复杂度，${\rm C}$不是合法的次模复杂度量。但是可以证明对任意函数$f$和任意次模复杂度量$\mu$，有$\mu(f) \le {\rm C}(f)$。这提示了一个证明比较器电路的复杂度下界的方法：构造一个次模复杂度量，然后证明这个度量在$f$上很大！然而，Razborov证明了所有次模复杂度量在所有函数上的值都不超过$O(n)$，所以这种方法证不出$\omega(n)$的比较器电路下界。

对偶定理：这篇文章证明了$f$的均摊复杂度恰好等于形式化复杂度量在$f$上的最大值。这里，$f$的“复杂度”和“形式化复杂度量”的定义都和具体的计算模型有关。（比如比较器电路对应次模复杂度量，于是$f$的比较器电路均摊复杂度恰好等于$\max_\mu \mu(f)$，其中$\mu$取遍所有的次模复杂度量。）这个结论是通过线性规划的对偶原理证明出来的。

于是，上述Razborov关于次模复杂度量的结果有如下推论（看上去可能很惊讶）：对任意函数$f$，存在一个整数$m$，使得我们只需要$O(mn)$大小的比较器电路就能计算出$f^m$。（作为对比，如果我们只想计算一个$f$，我们会需要大概$2^n$大小的电路！）当然，这里的$m$将会是一个非常大的数。

催化剂算法：一般的${\sf LOGSPACE}$图灵机只有两个纸带：一个只读的输入纸带和一个长度只有$O(\log n)$的工作纸带。现在假设我们给图灵机安上了第三个纸带，它的长度无限、可读可写，但是有一个要求：初始状态下这个纸带上的内容是任意的，且算法结束后纸带上的内容必须和初始时一样。这个模型有一个很形象的名字——催化剂算法（catalytic algorithms），因为第三个纸带很像化学反应里的催化剂。令人惊讶的是，带催化剂纸带的${\sf LOGSPACE}$能够计算${\sf TC}^1$的所有函数（所以很可能比原来的${\sf LOGSPACE}$更强）！

${\sf LOGSPACE}$对应的电路类型叫“分支程序”（branching program）。催化剂${\sf LOGSPACE}$对应着如下模型的分支程序：令$m$为催化剂纸带的长度，我们有$2^m$个起点$s_1, s_2, \dots, s_{2^m}$、$2^m$个表示“接受”的点$a_1, a_2, \dots, a_{2^m}$、以及$2^m$个表示“拒绝”的点$r_1, r_2, \dots, r_{2^m}$。对任意输入$x$，如果我们接受$x$，那么每一个$s_i$都能走到对应的$a_i$；如果拒绝$x$，那么每一个$s_i$都能走到对应的$r_i$。（注意每个$s_i$都只能走到$a_i$或者$r_i$，不能走到其他的$a_j$或$r_j$。）

Potechin证明了任何函数$f$都能被一个$O(mn)$大小的催化剂分支程序计算，其中$m = 2^{2^n - 1}$。这篇文章将$m$的上界改进到了$2^{\binom{n}{\le d}}$，其中$d$是$f$作为一个${\rm GF}(2)$-多项式的度数。

一些讨论：对于哪些复杂度$C$和哪些函数$f$，我们能给出较小的$m$使得$C(f^m) \ll m\cdot C(f)$？目前的结果中$m$好像都很大（$2^{2^n}$级别）。瞎猜：或许这个问题和所谓的mass production theorem（Ingo Wegener的教材 Sec 10.2）有关？

Fooling Constant-Depth Threshold Circuits

（5月7日诈尸更新）

令${\sf TC}^0_d[w]$表示深度为$d$的、$w$条线的${\sf TC}^0$电路，其中每个门都是一个${\sf LTF}$门。（一个${\sf LTF}$门接受输入$x\in\{0, 1\}^n$当且仅当$\sum_{i=1}^n w_i\cdot x_i \ge \theta$，其中$w_1, w_2, \dots, w_n, \theta$是这个门的参数。有的研究者也管它叫${\sf THR}$门。）对于这样的电路，我们目前能够证明的最好的下界是$n^{1+2^{-O(d)}}$。这篇文章给出了与这一下界相匹配的PRG；具体地说，令$\delta = 2^{-O(d)}$，这个PRG的种子长度为$n^{1-\delta}$，且能够$2^{-n^\delta}$-愚弄${\sf TC}^0_d[n^{1+\delta}]$。我最近听了听这篇文章对应的视频，于是写个笔记稍微记录一点技术。

假设我们有一个电路类$\mathscr{C}$，我们可以用以下方法构造其PRG（好像是Ajtai-Wigderson提出来的）：

• 首先，搞一个伪随机的restriction，使得这个restriction大概率把$\mathscr{C}$中的电路变成某个更简单的类里面的电路。把这个更简单的电路类叫做$\mathscr{C}_{\rm simple}$。
• 然后，搞一个$\mathscr{C}_{\rm simple}$的PRG。
• 最后，我们把这个伪随机的restriction和$\mathscr{C}_{\rm simple}$的PRG合并起来（这里我还不太会），就能得到$\mathscr{C}$的PRG啦。

这篇文章的一个很重要的贡献是定义出一个好的$\mathscr{C}_{\rm simple}$：伪随机的restriction要能够把${\sf TC}^0_d$变成$\mathscr{C}_{\rm simple}$，而且我们也得有$\mathscr{C}_{\rm simple}$的PRG。我们不能直接取$\mathscr{C}_{\rm simple} = {\sf TC}^0_{d-1}$（就是少一层的${\sf TC}^0$电路），因为我们并不知道怎么把${\sf TC}^0_d$电路简化成${\sf TC}^0_{d-1}$电路。事实上，文章定义的$\mathscr{C}_{\rm simple}$是一个（人类看上去并不简单的）决策树模型，这个决策树可以询问一些变量和一些${\sf LTF}$（询问次数分别有一定的限制），而且决策树的每个叶子都是${\sf TC}^0_{d-1}$电路。管这种模型叫做“${\rm DT}\text{-}{\sf TC}^0$”（${\rm DT}$代表Decision Tree），可以证明伪随机的restriction能够把${\rm DT}\text{-}{\sf TC}^0_d$简化成${\rm DT}\text{-}{\sf TC}^0_{d-1}$。当我们用了$d-1$次restriction之后，整个计算模型变成了${\rm DT}\text{-}{\sf LTF}$（也就是说决策树的叶子也是${\sf LTF}$了）。于是，我们还需要对${\rm DT}\text{-}{\sf LTF}$这个“简单”的模型造一个PRG。

那么这篇文章最重要的问题是如下两个：（1）如何用restriction把${\rm DT}\text{-}{\sf TC}^0_d$简化为${\rm DT}\text{-}{\sf TC}^0_{d-1}$，以及（2）如何搞一个${\rm DT}\text{-}{\sf LTF}$的PRG。

先讲（1）。我们可以证明在一个伪随机的restriction下，一个${\sf LTF}$函数有很大概率变成一个很biased的函数（就是说要么在绝大多数输入上都会输出$0$，要么在绝大多数输入上都会输出$1$）。于是，我们用一个伪随机的restriction去简化最底层的所有${\sf LTF}$，从而把深度减少$1$。如果一个${\sf LTF}$变得很biased，我们把它换成对应的那个常数就行，得到的简化的电路和原电路是“接近”的。现在的问题是“${\sf LTF}$会变成biased函数”的这个概率并不是特别大，所以无法用union bound。——也就是说，最底层还是会有一些${\sf LTF}$还不是很biased，因此我们无法干掉它们。我们需要在决策树上把这些不太biased的${\sf LTF}$都询问掉；根据这些${\sf LTF}$长什么样，文章中用了一些分类讨论来决定到底是询问单个的变量还是直接询问对应的${\sf LTF}$。这部分据说技术细节很复杂，我没有仔细搞懂。

然后是（2）。我们可以把${\rm DT}\text{-}{\sf LTF}$写成一堆${\sf AND}\circ{\sf LTF}$的和，然后我们只需要造一个${\sf AND}\circ{\sf LTF}$的PRG就行了。${\sf AND}\circ{\sf LTF}$又称“polytope”，有很多论文研究这种东西的PRG。但是有一个问题：这篇论文需要误差非常小（$2^{-n^{0.99}}$）的PRG，前人的PRG都做不到这个误差，所以必须重新设计。这篇文章用到的性质是：${\sf LTF}$的通信复杂度很小！于是我们可以直接用通信协议的PRG。但是因为${\sf LTF}$只是随机通信复杂度很小（而不是确定通信复杂度），所以我们还需要用Sherstov的一些技术，具体我也没太看。

我觉得这个决策树模型看上去很有潜力，说不定可以做各种其他电路的PRG？毕竟如果伪随机的restriction没有把电路简化得干干净净，我们只要把“不干不净”的地方挨个询问一遍就行了。。。