STOC 2022 游记

吗的我签证又被卡了，不管了假装老子去STOC开心地玩了几天

The Shortest Even Cycle Problem is Tractable

推特上说这篇文章的talk讲得很妙！我去看了一下，果真名不虚传。

这篇文章考虑的问题是shortest even cycle problem：给出一张有向图，求其中最短的长度为偶数的简单环。这篇文章给出了一个多项式算法。这个问题可能比第一眼看上去要难一些，事实上，它的一些简化版已经是很经典的难题了：

• shortest cycle problem（最短的简单环）：只要不断对图的邻接矩阵求幂即可。设图的邻接矩阵为$A$，那么我们只需要求出满足$A^k$的迹不为$0$的最小的$k$即可。邻接矩阵的幂反映的是walk（可以自交的环）的数量，但是因为最短的walk也是最短的cycle，所以这么做是可行的。
• shortest odd cycle problem（最短的长为奇数的简单环）：照样求出$A^k$的迹不为$0$的最小的$k$即可。因为最短的长为奇数的walk也是最短的长为奇数的cycle，所以这么做也是可行的。
  注意，最短的长为偶数的walk不一定是个cycle（比如，它可能可以分解成两个长为奇数的cycle和一个公共顶点），所以直接矩阵求幂不能解决shortest even cycle problem。
• undirected shortest even cycle problem（无向图中最短的长为偶数的简单环）：这个问题已经不简单了——我们可以把它规约到一般图最大匹配解决。后来Yuster和Zwick给出了一个$O(n^2)$时间的算法。
• even cycle（判断是否存在长为偶数的简单环）：这是一个很经典的问题，又称Pólya's permanent problem。给出一个0/1矩阵$A$，能否把$A$里面的一些$+1$元素改成$-1$，得到一个矩阵$B$使得${\rm per}A = \det B$？这个问题和如下问题是等价的：（1）给出一个有向图，问其中是否存在长度为偶数的简单环？（2）给出一个由$+,-,0$组成的矩阵，是否可以把$+$换成正实数、$-$换成负实数，使得得到的矩阵可逆？（3）给出一个矩阵，其行列式和积和式是否相等？（4）给出一张无向图，问其是否存在Pfaffian orientation？
  这个问题在1913年被Pólya提出，但是直到1999年才由Robertson、Seymour、Thomas发现多项式算法。

本文的技术如下：设$A$为图的邻接矩阵，那么${\rm per}(I+A) - \det (I+A)$能够统计图中长为偶数的简单环的数量。但是，${\rm per}$是难以计算的，所以我们需要找一个环使得其中积和式变得容易计算。为了求得最短的环，我们需要加入一个形式化变量$x$，并求出${\rm per}(xI+A) - \det(xI+A)$作为一个多项式的最高次项。于是我们需要用一些插值（把$x$代入不同的值）来求出这个多项式。很可惜的是，我们并不知道什么样的环同时满足“积和式容易计算”以及“可以搞插值”。于是，我们在域$\mathbb{Z}_2[x]/\langle g\rangle$中搞插值（$g$是一个度数为$O(\log n)$的不可约多项式，这个域等于${\rm GF}(2^{O(\log n)})$），在环$\mathbb{Z}_4[x]/\langle g\rangle$中计算积和式，然后根据这两个代数结构之间的一些联系来求出目标多项式的最高次项。（orz这就是视频中有提及的部分了，我没看文章所以肯定没有理解清楚

Pseudodeterminism: Promises and Lowerbounds

这篇文章研究了伪确定性算法。我们考虑如下问题（原文中称作${\sf APEP}$，但是我更习惯称作${\sf CAPP}$）：给出一个电路$C$，估算$\Pr_x[C(x) = 1]$，要求绝对误差不超过$\epsilon$。伪确定性算法领域的一个重要open problem是${\sf CAPP}$的（多项式时间）伪确定性算法的存在性。如果${\sf CAPP}$有伪确定性算法，那么我们可以推出很多关于随机复杂度的结论，例如${\sf BPP}$时间分层定理、${\sf BPP}$-完全问题的存在性、电路复杂度下界（${\sf MA}\not\subseteq{\sf SIZE}[n^{100}]$）等。与此同时，这个问题有一个显然的$2$-伪确定性算法，也就是说大概率会输出某两个正确答案中的一个的算法：在估算$C$接受一个随机输入的概率之后，将其截取至最接近的$\epsilon$的整数倍。

我们可以考虑如下叫做$2$-${\sf CAPP}$的问题：给出两个电路$C_1, C_2$，分别估算其接受随机输入的概率。显然，这个问题有一个$4$-伪确定性算法：对这两个电路分别跑上述$2$-伪确定性算法即可。Goldreich证明了这个问题也有一个$3$-伪确定性算法。本文证明了在某种询问模型下（就是我们只能在某种意义上把这两个电路当成黑盒子用）这个问题不存在多项式时间的$2$-伪确定性算法。

证明是这样的。假设我们有一个$[0,2^n]\times [0,2^n]$的网格，其中坐标为$(i,j)$的点对应如下输入$(C^i, C^j)$：$C^i$接受前$i$个输入并拒绝其他输入，$C^j$接受前$j$个输入并拒绝其他输入。在文中所考虑的询问模型中，可以证明如下引理：设$(i_1,j_1)$和$(i_2,j_2)$相邻，$A$是一个$q$次询问的询问算法，那么$A(C^{i_1}, C^{j_1})$和$A(C^{i_2}, C^{j_2})$（作为两个随机变量的概率分布）的total variation distance不超过$q/2^n$。

现在，我们给每个$[0, 1]\times [0, 1]$中的实数对染上三种颜色，染色的方法如上图所示。接下来，对每个点$(i,j)$，设我们的伪确定性算法$A$在$(C^i,C^j)$上的概率最高的输出是$(p_1, p_2)$，那么我们给这个点染上$(p_1, p_2)$的颜色。总之，重要的是$(0,0)$、$(0,2^n)$、$(2^n,0)$染上了三种不同的颜色。接下来我们使用Sperner's lemma，得到至少有一个小正方形$(i,j)-(i+1,j+1)$的四个顶点中有三种不同的颜色。不妨假设$(i,j)$、$(i,j+1)$、$(i+1,j)$的颜色两两不同。假设$A$在$(C^i,C^j)$上的概率最高的输出是$(p_1,p_2)$，在$(C^i,C^{j+1})$上的概率最高的输出是$(p_3,p_4)$，在$(C^{i+1},C^j)$上的概率最高的输出是$(p_5,p_6)$。由于$A$是个$2$-伪确定性算法，$A$在$(C^i,C^j)$上输出$(p_1,p_2)$的概率至少是$3/8$。同理，$A$在$(C^i,C^{j+1})$上输出$(p_3,p_4)$的概率至少是$3/8$，所以由刚刚的引理，$A$在$(C^i,C^j)$上输出$(p_3,p_4)$的概率至少是$3/8-q/2^n$。同理，$A$在$(C^i,C^j)$上输出$(p_5,p_6)$的概率也至少是$3/8-q/2^n$。因为$(p_1,p_2)$、$(p_3,p_4)$、$(p_5,p_6)$两两不同，所以$A$在$(C^i,C^j)$上输出某个值的概率为

\[3/8 +(3/8-q/2^n) + (3/8-q/2^n) = 9/8-2q/2^n > 1,\]

矛盾。

感觉伪确定性算法的询问复杂度下界是个很有意思的研究方向（

Worst-Case to Average-Case Reductions via Additive Combinatorics

视频讲得很清楚！

本文中考虑对矩阵乘法问题做平均复杂度规约。假设我们有一个算法${\sf ALG}$，它能够在$\alpha = 1\%$的输入上解决矩阵乘法，即：

\[\Pr_{A, B\gets \mathbb{F}_2^{n\times n}}[{\sf ALG}(A, B) = AB] \ge \alpha.\]

我们想要搞一个算法${\sf ALG}'$，使得它能在最坏情况下解决矩阵乘法，即对于所有的$A,B\in\mathbb{F}_2^{n\times n}$，

\[\Pr[{\sf ALG}'(A, B) = AB]\ge 2/3.\]

在这里为简单起见，我们只考虑对$B$做规约。也就是说假设$A$是“好的”——即$\Pr_B[{\sf ALG}(A,B)=AB]\ge\alpha$，搞一个能对所有$B$计算$AB$的算法。

令$X$为“好的”$B$的集合，即满足${\sf ALG}(A,B)=AB$的矩阵的集合。根据Freivalds算法，在算出了${\sf ALG}(A,B)$之后，我们可以在$\tilde{O}(n^2)$时间内验证算出来的结果是否等于$AB$。于是我们可以快速地验证某个$B$是否在$X$中。

这篇文章用到的加性组合的引理是这样的（其中，根据加性组合的惯用记号，定义$4X=\{x_1+x_2+x_3+x_4:x_1,x_2,x_3,x_4\in X\}$）：

事实上，我们需要上述引理的一个加强版。上述引理说的是$4X$中可以找到一个比较大的线性空间，但是我们需要一个更强的性质：线性空间中的每个元素都有很多种表示为$x_1+x_2+x_3+x_4$（$x_1,x_2,x_3,x_4\in X$）的方法。

那么我们可以描述我们的平均复杂度规约了。因为$X$是$\mathbb{F}_2^{n\times n}$中的密度为$\alpha$的子集，所以令$k=1/O(\log^4(1/\alpha))$，存在一个维度至少为$n^2-k$的线性空间$V$，满足上述概率Bogolyubov引理的结论。我们随机一个秩为$k$的矩阵$L$，那么$B-L\in V$的概率至少是$2^{-O(k)}$。如果$B-L\in V$，那么我们可以随机四个矩阵$M_1, M_2, M_3, M_4$，使得其加起来等于$B-L$。以$\alpha^5$的概率，这四个矩阵都在$X$中。如果上述事件均成立，那么

\[AB = AL + A(B-L) = AL + \sum_{i=1}^4{\sf ALG}(A, M_i).\]

因为$L$的秩只有$k$，所以我们可以在$O(n^2k)$时间内算出$AL$。因为每个$M_i$都在$X$中，所以我们可以用${\sf ALG}$算出$A\cdot M_i$。于是，我们的算法就可以以$2^{-O(k)}\cdot \alpha^5=2^{-{\rm polylog}(1/\alpha)}$的概率算出$A\cdot B$。因为我们有Freivalds算法，所以我们可以验证算出的$A\cdot B$是不是对的；重复上述算法$2^{{\rm polylog}(1/\alpha)}$次之后即可得到正确的$A\cdot B$。

问题：可以把这个算法当成某种纠错码的list-decoding算法吗？

Reproducibility in Learning

本文提出了“复现”（reproducibility）的概念。假设我们有一个算法$A(S, r)$，其中$S$是从某个分布$\mathcal{D}$中采样出来的一堆iid sample（例如$A$是个机器学习算法，$S$是它的训练集），$r$是算法用的internal randomness。我们说$A$是$\rho$-可复现的，如果

\[\Pr_{S_1, S_2\gets \mathcal{D};~r}[A(S_1, r) = A(S_2, r)] \ge 1-\rho.\]

换句话说：$A$的输出只和其internal randomness有关，和它收到的“训练集”无关。

我们可以把可复现算法和伪确定性算法这两个概念做一个对比。伪确定性算法的输入是一个（最坏情况的）串$x$和随机串$r$，其输出和$r$无关；可复现算法的输入是一个采样$S$和随机串$r$，其输出可以和$r$有关，但是和“训练集”$S$无关。

这篇文章证明了很多与可复现算法有关的结果。我觉得以下两个结果比较有意思：

• 一个可复现的估算$\mathcal{D}$的中位数的算法。假设$\mathcal{D}$是有序集$(X, <)$上的分布，我们希望找一个元素$x_{\rm mid}$使得$\Pr_{x\gets \mathcal{D}}[x < x_{\rm mid}] \ge 1/2-\epsilon$，并且$\Pr_{x\gets \mathcal{D}}[x > x_{\rm mid}] \ge 1/2-\epsilon$。我们可以通过从$\mathcal{D}$中采样若干（iid）元素来帮我们估算$x_{\rm mid}$。“可复现”的意思是：不论我们收到什么样的样本，算法输出的$x_{\rm mid}$只和其internal randomness有关，和我们收到的样本无关。
  基于这个算法，作者提出了一个可以把一般的算法变成可复现算法的模板。假设正确答案是$ans$，可以接受的答案范围是$[ans-\epsilon, ans+\epsilon]$，算法$B(S, r)$能够以大概率输出一个可以接受的答案，但是$B$不一定是可复现的。如果我们想要可复现地求出一个可以接受的答案，我们只要跑很多遍$B(S, r)$，然后套用上面的算法，可复现地求出这些答案的中位数即可。
• 一个可复现的boosting算法，它可以将一个可复现的weak learner（正确概率$1/2+\epsilon$）变成一个可复现的strong learner（正确概率$1-\delta$）。基于这个算法和一些其他的技术，作者给出了一个可复现的学习半平面的算法。

Locally Testable Codes with constant rate, distance, and locality

只讲一下是怎么构造的，不讲证明（

这个构造中需要用到的工具叫“左右Cayley复形”（left-right Cayley Complex）。设$G$是一个群，$A,B$是$G$的子集，且均对求逆运算封闭（例如，$a\in A\implies a^{-1}\in A$）。左右Cayley复形${\rm Cay}^2(A,G,B)$包含如下的点、边、面：

• $G$中的每个元素称作一个点。
• 对任意$g\in G$、$a\in A$，我们在$g$和$ag$之间连一条（红色的）边。
• 对任意$g\in G$、$b\in B$，我们在$g$和$gb$之间连一条（蓝色的）边。
• 对任意$g\in G$、$a\in A$、$b\in B$，我们称$\{g,ag,gb,agb\}$为一个面。
  注意：任意一个面包含$4$条边和$4$个点。我们可以用$(a,g,b)$表示一个面，这样的话每个面有四种表示方式（$(a,g,b)$、$(a^{-1},ag,b)$、$(a^{-1},agb,b^{-1})$、$(a,gb,b^{-1})$）。

如何选取$A,G,B$呢？我们希望${\rm Cay}(A,G)$和${\rm Cay}(G,B)$都是expander，其中${\rm Cay}(A,G)$为所谓的Cayley图：顶点集合为$G$，边集为上面定义的“红边”（也就是$\{(g, ag):g\in G, a\in A\}$）。满足$|A|,|B|=O(1)$，且${\rm Cay}(A,G)$和${\rm Cay}(G,B)$都是expander的构造是已知的。然后，我们考虑如上定义的左右Cayley复形${\rm Cay}^2(A,G,B)$。此外我们还需要两个（常数大小的）纠错码$C_A\subseteq\{0, 1\}^{|A|}$和$C_B\subseteq\{0, 1\}^{|B|}$。

我们的LTC中，每个codeword的长度为面的个数（也就是$|G|\cdot |A|\cdot |B|/4$）。每个面上有一个bit。每条边是一个约束：对于一条红边$(g,ag)$，如果我们把所有形如$(a,g,b)$的面上的bit连在一起（形成一个长度为$|B|$的串），那么要求这个串在$C_B$中。蓝边同理。我们的LTC就是所有满足这些条件的codeword组成的集合。

显然rate是常数。通过一些expander code相关的计算可以得知distance是常数。local tester长这样：随机选一个点（不是一条边！），然后检查包含它的$|A|\cdot |B|$个面上的所有bit在tensor code $C_A\times C_B$里面。

The Query Complexity of Certification

这篇文章的结果被改进到最优了！改进的算法很简单所以我只讲改进的算法。

问题是这样的。给出一个单调的函数$f:\{0, 1\}^n\to\{0, 1\}$以及一个输入$x^\star$，设$k=C(f)$为$f$的certificate complexity，我们希望找到$x^\star$的一个大小为$k$的certificate。假设$f$是个黑箱子，我们希望用尽量少的对$f$的询问来解决这个问题。可以证明这个问题需要$\Omega(k\log n)$次询问才能解决。Angluin给出了一个$O(n)$次询问的算法，今年STOC的论文做到了$O(k^8\log n)$次询问，改进的算法只需要最优的$O(k\log n)$次询问。

注意：在这个问题中，$k$是$f$的certificate complexity，而不是$f$在输入$x^\star$上的certificate complexity。如果我们需要找到$x^\star$的大小为$C(f,x^\star)$的certificate，那么需要$\Omega(\binom{n}{k})$次询问，远大于本文中的$O(k\log n)$次询问。

简单起见我们做如下假设：

• 我们把一个串（$x$）和它值为$1$的下标构成的集合（$\{i:x_i = 1\}$）一一对应起来。这样，我们可以用集合的记号来操作这些串，例如“$f$是单调的”可以写成“$x\subsetneq x', f(x) = 1\implies f(x') = 1$”。
• 假设$f(x^\star) = 1$。这是因为如果$f(x^\star) = 0$，那么我们可以考虑$g(x) = 1-f([n]\setminus x)$。

算法是这样的：我们维护一个串$x'$，初始时为全$0$串。当$f(x') = 1$时算法结束。每次我们会选一个最小的$i$使得$f(x' \cup ([i]\cap x)) = 1$，然后把$i$加入进$x'$里面去。由于$f$是单调的，我们可以用二分查找在$O(\log n)$次询问内找出这个$i$。设最终$x'$的大小为$k'$（也就是有$k'$个$1$），我们算法的复杂度显然是$O(k'\log n)$。

接下来我们只需要证明$C(f)\ge k'$。这几乎是显然的：对于$x'$中的任意一个元素$i$，我们都有$f(x'\setminus\{i\}) = 0$，所以$C(f,x') = k'$。于是我们算法的复杂度就是$O(C(f)\cdot \log n)$了。

Maintaining Exact Distances under Multiple Edge Failures

是我参与了的paper！给出一张无向带权图$G$，要求支持如下询问：每次询问给出点$u,v$和$d$条故障边$D$，我们想知道从$u$走到$v$不经过$D$的最短距离的值。之前的工作要么只能处理$d=2$条故障边，要么只能求出$(1+\epsilon)$-近似的最短距离，要么需要$n^{\Omega(1)}$的询问时间。

我们给出了一个数据结构，它能够处理任意$d$条故障边、能够求出精确的最短距离、大小为$O(dn^4)$、询问复杂度为$d^{O(d)}$。（也就是说当$d$是常数时，询问复杂度也是常数！）

不是很清楚这个结果意味着什么。。。毕竟之前大家一直觉得在多于$2$个故障的时候，维护精确的最短距离可能是很难的。现在我们发现了一个非平凡的处理$d$条故障边的做法，这说不定暗示着故障点也是可以处理的？Fault-tolerant distance oracle实际上比大家想象得要简单些？

技术不是很好讲（

Constant Inapproximability for PPA

没有听懂技术细节，所以把题目复述一下吧。我们的问题叫做Consensus Halving。想象区间$[0,1]$是一块蛋糕，我们要把这块蛋糕分给$n$个人。每个人都有自己对这块蛋糕每一部分的“价值”。（可以理解为第$i$个人有一个函数$f_i$，他觉得区间$[l,r]$的“价值”就是$\int_l^rf_i(x){\rm d}x$。）不妨假设每个人对整块蛋糕$[0,1]$的价值都等于$1$。现在要求将蛋糕切$n$刀切成$n+1$个部分，然后将一些部分标为“$+$”、一些部分标为“$-$”，并且使得每个人对“$+$”部分的价值和对“$-$”部分的价值之差不超过$\epsilon$。

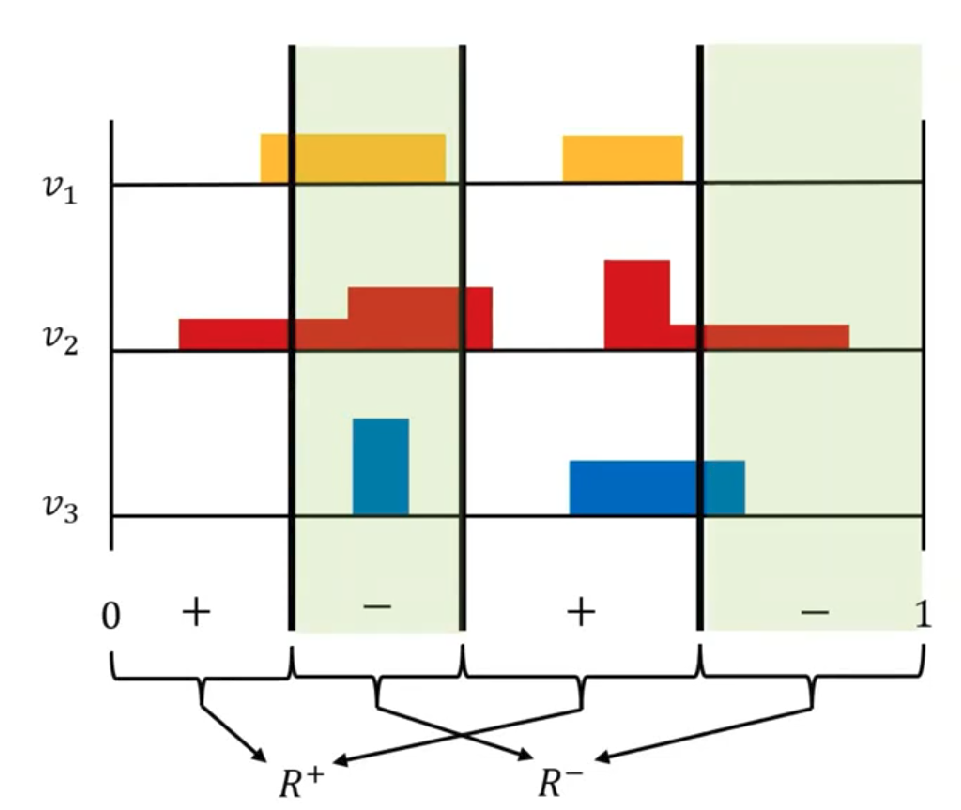
可以用Borsuk-Ulam定理证明当$\epsilon = 0$时（每个人对“$+$”部分和“$-$”部分的估值都必须正好为$1/2$），总是存在一个切$n$刀的分法。同时，$n$刀是必须的（考虑第$i$个人只对区间$[i/n,(i+1)/n]$内的部分感兴趣的情况，每个人感兴趣的部分你都至少得切一刀）。

假设每个$f_i$都是piecewise constant，那么$\epsilon = 0$时这个问题是${\sf PPA}$-完全的。本文证明了这个问题在$\epsilon < 1/5$时也是${\sf PPA}$-完全的。这是${\sf PPA}$-完全问题中的第一个hardness of $\Theta(1)$-approximation的结果。

The Exact Complexity of Pseudorandom Functions and the Black-Box Natural Proof Barrier for Bootstrapping Results in Computational Complexity

这篇文章包含两个结果：（1）PRF的复杂度可以做到非常低，几乎等于算${\sf PARITY}$的复杂度；（2）文章同时还给出了一个black-box natural proof barier，用于解释最近的bootstrapping result（例如CT19和CJW20）为什么没能被用来证breakthrough lower bounds。

首先需要澄清一下这里PRF的定义。传统的PRF会输入一个key $k$和一个输入$x$，但是我们如果输入$k$的话会使得电路复杂度变大。（这篇文章对PRF的电路复杂度要求非常紧！）所以，这篇文章中的PRF实际上指的是布尔函数的分布${\cal F}$，使得每个${\cal F}$中的函数的电路复杂度都很小，并且${\cal F}$和随机函数是难以区分的。我们可以认为$k$是对$\cal F$进行采样时使用的随机串；我们只要求对于每个确定的$k$，我们采样出的函数的复杂度很小。

文章的第一个结果：PRF的复杂度基本上和${\sf PARITY}$的复杂度一样。在这里我们只记录$B_2$电路中的结果：如果存在PRF，那么存在电路复杂度只有$2n+o(n)$的PRF。（文章中对${\sf TC}^0$电路和${\sf AC}^0[2]$电路也都给出了结果。）

首先，如果存在PRF，那么存在电路复杂度为$O(n)$的PRF。构造如下：令$h:\{0, 1\}^n\to\{0, 1\}^{n^\epsilon}$为一个universal hash function。如果$f(x)$是一个PRF，那么$f(h(x))$也是一个PRF。注意到$h$将输入长度从$n$缩短到了$n^{\epsilon}$，所以如果$f$的电路复杂度是$n^k$，那么我们取$\epsilon = 1/2k$即可将总的电路复杂度做到$H+n^{\epsilon k}=H+o(n)$，其中$H$是哈希函数的电路复杂度。由于我们可以在$O(n)$大小中构造universal hash function，所以$H=O(n)$，也就是存在电路复杂度为$O(n)$的PRF。

但是我们不知道怎么在$2n$的电路复杂度中构造universal hash function。这篇文章的亮点是：我们只需要$h$为“almost universal hash function”，上述构造仍然可以保证PRF的安全性。接下来，这篇文章在$2n+o(n)$的复杂度中构造出了almost universal hash function。因为构造不是很难所以我详细记录一下：

• 首先，我们需要一个girth很高的图：对任意$m,k$（其中$k<m/3$），我们可以确定性地构造一个$m$个点、$\lfloor mk/2\rfloor$条边，且girth至少为$g>\log_k m+O(1)$的图。并且，每个点的度数在$k-1,k,k+1$中。这里我们取$k = O(\log n), m = 2n/k$，于是得到的图的点数为$o(n)$，边数为$n$。
• 然后，我们把这个girth很高的图变成一个“randomized $1$-detector”。设$r,m<n$为两个参数，一个$1$-detector是指一个电路$C:\{0, 1\}^n\to\{0, 1\}^m$（可以理解成一个code的parity-check电路），使得对任意$x\in\{0, 1\}^n\setminus\{0^n\}$，如果$x$中至多有$r$个$1$，那么$C(x)\ne 0^m$。一个“randomized $1$-detector”会在把$x$喂给$C$之前将其所有位随机排列（记排列后的串为$\rho(x)$），然后只要求$C(\rho(x))\ne 0^m$大概率是对的就行了。
  假设我们有一个girth很高的图。我们的电路$C$把$x$的输入放在边上，然后每个点输出其所有邻边的异或。如果图的girth很高，那么这样能得到一个不错的randomized $1$-detector。
• 接下来，我们把randomized $1$-detector变成一个“almost universal hash function”。这个哈希的key是一个排列$\rho$和一个大小为$O(\log^2 n)$的子集$S=\{i_1, i_2, \dots, i_s\}$，设$C$为我们的randomized $1$-detector，定义
  \[h_{\rho,S}(x) = x_{i_1}x_{i_2}\dots x_{i_s}\circ C(\rho(x)).\]
  可以证明这是个almost universal hash function，即对任意$x\ne y$，我们有$\Pr_{\rho, S}[h_{\rho, S}(x) = h_{\rho, S}(y)] \le {\rm negl}(n)$。这个hash function将$n$个输入映射到$m = o(n)$个输出，且可以用$2n+o(n)$大小的电路计算。

如果存在PRF，那么我们可以用universal hash来得到一个大小为$O(n)$的PRF。接下来我们把这个$O(n)$大小的PRF套在almost universal hash的输出上（输出长度为$m=o(n)$，所以电路复杂度为$O(m) < o(n)$），就可以得到一个大小为$2n + o(n)$的PRF。

最后，这个hash的每个输出位都只等于一些输入位的${\sf PARITY}$。所以PRF的复杂度不会比${\sf PARITY}$的复杂度高出太多。

文章的第二个结果：bootstrapping result + 所谓的black-box natural proof不能用来证breakthrough。很多的bootstrapping result（比如我刚刚提的CT19和CJW20）形如“如果我们能够证明某个问题需要大小为$s$的电路，那么能证某种breakthrough（比如${\sf NEXP}\not\subseteq{\sf NC}^1$）”。另一方面，考虑某种能够证明大小为$s'$的电路复杂度下界的方式。如果$s' > s$，那么我们可以把bootstrapping result和复杂度下界合并起来，然后推出breakthrough。但是在我们已知的结果中，$s'$总是小于$s$。为什么我们没法把这两者合并起来呢？

文章指出：对于很多bootstrapping result，由于证明技术的原因（证明中会用到hash），$s$总是会比$H$大一点点，其中$H$为“最小的almost universal hash”的大小。（例如对于$B_2$电路，$H=2n+o(n)$。）而很多电路复杂度下界是“black-box natural”的——也就是说它们会附带着证明大小为$s'$的PRF不存在。假设（多项式大小）PRF存在，那么大小$\approx H$的PRF也存在。于是我们有$s\ge H$而$s' < H$。所以，如果我们有一个“使用hash”的bootstrapping result和一个“black-box natural proof”，那么我们必然有$s' < s$，也就是我们无法把“使用hash”的bootstrapping result和“black-box natural proof”合并在一起并推出breakthrough。

Hardness of Approximation in P via Short Cycle Removal: Cycle Detection, Distance Oracles, and Beyond

技术没太听懂，感觉是某种structure vs randomness。但是这paper的结论太强了，所以我把结论摘抄一下（

我们使用triangle finding假设的如下变种：在度数为$\sqrt{n}$的图中寻找一个三角形需要$n^{2-o(1)}$时间。这个变种貌似并不是fine-grained complexity里面的标准假设，所以我们不知道它有多plausible；但是，如果我们要求对每条边都找到一个包含它的三角形（我们管它叫“all-edge version”），那么这个问题同时是3SUM和APSP-困难的。这篇文章证明了：

• 如果all-edge triangle finding假设是对的，那么任何$k$-近似的distance oracle都至少需要$m^{\Omega(1/k)}$的询问时间。
• 如果triangle finding假设是对的，那么我们需要至少$\Omega(m^{1.194})$的时间才能找到一张图的四元环。

文章的主要技术是一个triangle finding到自己的规约。这个规约保证规约后得到的图里面四元环很少（甚至有的情况下可以做到没有四元环）。

Robustness of Average-Case Meta-Complexity via Pseudorandomness

也是我参与了的paper（

我们研究了meta-complexity中一些问题的平均复杂度。与LP20不同的是，我们研究的是相对于${\rm PSamp}$（也就是可以多项式时间采样的分布）的复杂度，而LP20研究的是相对于均匀随机分布的复杂度。我们证明了${\rm GapK}$（近似计算Kolmogorov复杂度）和${\rm GapK}^{\rm poly}$（近似计算${\rm K}^{\rm poly}$复杂度）在${\rm PSamp}$下的平均复杂度可以由单向函数刻画。（${\rm GapK}^{\rm poly}$的结果需要一些去随机化假设。）

标题中的robustness指的是我们的等价性对于meta-complexity中的大量问题都成立。给meta-complexity中的不同问题之间进行相互规约一直都是这个领域的难题，我们的结果给出了平均复杂度下非常多的这样的规约！说起来，我们的规约既能够提升近似比（从$\omega(\log n)$到$n^{1-\epsilon}$），又能够提升平均复杂度（从$1-1/n$到$1/2+{\rm negl}(n)$）。技术上来讲，我们把密码学的一些技术（例如HILL99）直接拿过来当黑盒子用，所以导致这些规约和一般的${\sf NP}$问题之间的规约好像还不太一样？我也不太清楚这个规约到底发生了什么（毕竟我不会HILL99），或许我们的做法可以对一般的${\sf NP}$中的问题做这种近似比和平均复杂度的提升？

此外有一些放飞自我的想法：我觉得这篇文章说不定可以用来排除Pessiland！如果一个问题$L$是${\sf NP}$-完全的，那么$L$在${\rm PSamp}$下是困难的当且仅当${\sf DistNP}\not\subseteq{\sf heurP}$。那么，（在去随机化假设下，）如果${\rm GapK}^{\rm poly}$是${\sf NP}$-完全的，那么${\sf DistNP}\not\subseteq{\sf heurP}$当且仅当存在单向函数。换句话说${\rm GapK}^{\rm poly}$的${\sf NP}$-完全性可以用来排除Pessiland。（Hirahara18证明了同一个问题的${\sf NP}$-完全性可以用来排除Heuristica！某种意义上来讲，我们的论文可以看成Hirahara18的Pessiland analogue。。。）

但是${\rm GapK}^{\rm poly}$的${\sf NP}$-完全性太难证了，我在想可不可以找一些实际上能证${\sf NP}$-完全性的meta-complexity问题然后跟我们的文章结合在一起看看会发生什么？例如我们可以找${\sf DNF}\text{-}{\sf MCSP}$然后排除一些${\sf DNF}$版本的Heuristica或Pessiland？（←纯口胡

此外我们还证明了${\sf MCSP}$在${\rm LSamp}$下的平均复杂度也能刻画单向函数，其中${\rm LSamp}$是所有locally samplable的分布。我猜这说明${\sf NP}$或者${\sf PH}$在${\rm LSamp}$下的平均复杂度说不定也是个不错的研究方向？（毕竟大部分已知的${\sf NP}$-完全性规约都挺local的。。。）能不能把${\rm PSamp}$换成${\rm LSamp}$然后研究对应的Pessiland？

Algorithms and Certificates for Boolean CSP Refutation: "Smoothed is no harder than Random"

不懂技术所以只讲结论。前人研究的“随机$k$-SAT”是这样的模型：我们有一个$k$-CNF，每个子句都是在所有可能的$\binom{n}{k}2^k$个子句中完全随机生成的。如果子句的个数大于$\Omega(n)$，那么这样的$k$-CNF大概率没有解。我们希望设计一个算法，输入一个$k$-CNF，要么输出“无解”要么输出“我不知道”。要求：

• 如果算法输出“无解”，那么输入的$k$-CNF必须真的无解；
• 算法对大部分$k$-CNF都输出“无解”。

可以把这种算法看成是某种验证一个$k$-CNF无解的启发式算法。前人最好的结果如下：对任意$\ell$，存在一个$n^{O(\ell)}$时间的算法能够验证$m$个子句的$k$-CNF无解，其中

\[m = O(\ell (n/\ell)^{k/2}).\]

本文考虑的是$k$-CNF的平滑复杂度（一种介于最坏复杂度和平均复杂度之间的模型）。在这个模型中，输入的$k$-CNF是按照如下方式生成的：

• 首先，我们有一个最坏复杂度意义下的$k$-CNF $\varphi$。我们不能提前知道这个$\varphi$。
• 然后，我们把$\varphi$的每个子句中的每个变量以$0.01$（某个小常数）概率取反，得到$k$-CNF $\varphi'$，并把$\varphi'$喂给算法。

然后，我们把“算法对大部分$k$-CNF都输出‘无解’”改成“对任意（最坏情况的）$\varphi$，算法对大部分$\varphi'$都输出‘无解’”。

本文把上述$n^{O(\ell)}$时间的算法推广到了平滑复杂度的情形。这个结果可能说明$k$-SAT的复杂度并不是来源于输入CNF的结构（underlying hypergraph）的，而是来源于哪些子句中哪些变量被取反了？

Proving as Fast as Computing: Succinct Arguments with Constant Prover Overhead

本文对${\sf Circuit}\text{-}{\sf SAT}$造了一个IOP和一个succinct argument。当我们输入一个电路$C$，想证明$\exists x, C(x) = 1$时，prover的复杂度就是$O(|C|)$的！当然，$C$的描述本身就需要$O(|C|\log |C|)$个bit，所以“prover的复杂度时$O(|C|)$”的意思其实是“对任意$C$，存在一个（根据$C$生成的）大小为$O(|C|)$的prover”。

本文的技术贡献是一个可以在线性时间内编码的multi-sumcheckable的纠错码。为了说清楚什么叫“multi-sumcheckable”，我们需要简单回顾一下${\sf IP} = {\sf PSPACE}$的证明。这个证明中利用了多项式的如下性质：给出一个度数较低的多项式$g(x_1, x_2, \dots, x_n)$和一个数$s$，我们可以在${\rm poly}(n)$时间的交互式证明中证明

\[\sum_{b_1\in\{0, 1\}}\sum_{b_2\in\{0,1\}}\dots\sum_{b_n\in\{0,1\}}g(b_1,b_2,\dots,b_n) = s.\]

我们可以把多项式当成一个纠错码（也就是Reed-Muller code）。记这个纠错码为$\cal C$，里面的每一个元素为一个低度数多项式$C:[N]\to\mathbb{F}$，并且令$t = 2^n$。那么对任意$C\in{\cal C}$，我们可以在远小于$t$的时间内交互式地证明$\sum_{i\in [t]}C_i = s$。这个性质叫做“sumcheck”性质，我们说Reed-Muller是“sumcheckable”的。一些其他的纠错码，例如tensor code，也是“sumcheckable”的。

在证明${\sf IP} = {\sf PSPACE}$以及构造其他的交互式证明时，我们实际上需要做的不是sumcheck，而是“multi-sumcheck”：给出两个$C_1, C_2\in{\cal C}$和$s\in\mathbb{F}$，我们希望能够快速地交互式证明

\[\sum_{i\in[t]} (C_1)_i \cdot (C_2)_i = s.\]

注意到如果$C_1$和$C_2$都是度数较低（$<d$）的多项式，那么$C_1\cdot C_2$也是度数较低（$< 2d$）的多项式。如果一个纠错码${\cal C}$满足$\{C_1\cdot C_2:C_1, C_2\in{\cal C}\}$也组成一个（参数可能稍微差一点的）纠错码，那么我们说${\cal C}$是积性（multiplicative）的。如果一个纠错码是积性的，而且它乘起来之后那个纠错码是sumcheckable的，那么我们可以对这个纠错码做multi-sumcheck。

很可惜的是，我们现在还不知道可以在线性时间内编码的积性纠错码。这篇文章对于纠错码的效率有着非常高的要求，所以目前已知的积性纠错码不能用于这篇文章。

这篇文章的最重要的技术是一个可以线性时间编码、也可以做multi-sumcheck的纠错码。（虽然这个纠错码并不是积性的。）并且，在对应的multi-sumcheck的协议中，prover可以用线性大小的电路实现。

Dynamic Algorithms workshop

去蹭了蹭workshop，发现对Amir Abboud讲的（一些open problem）和Jan van den Brand讲的（动态矩阵算法）比较感兴趣。

Amir提到了四种不同的动态算法模型，它们从容易到困难分别是：

• 离线算法。所有的修改和询问都提前告诉你，你只需要把它们一起处理就好。
• oblivious adversary。所有的修改和询问都是提前固定好的（虽然你并不提前知道）。
• adaptive adversary。adversary会根据你这次询问输出的答案来决定下一个询问是什么。（例如你的输出是某个满足条件的点或者路径，这个输出可能会和你的internal randomness有关，此时adversary就能针对你的internal randomness来卡你。）
• 确定性算法。要求你不能使用任何随机性。（如果你的算法是确定性的，那么oblivious adversary和adaptive adversary是等价的。）

问题：能否将这些模型分隔开？比如说找一个问题使得它在一个模型中比较容易，在另一个模型中比较困难。一些candidate：

• online matrix-vector multiplication：给出$n\times n$矩阵$A$，以及$n$个询问，每个询问是一个向量$v$，要求$Av$的值。如果是离线模型的话这个问题就是矩阵乘法，所以有均摊复杂度$O(n^{\omega-1})<O(n^{1.373})$的算法。在其他三种模型中，目前的猜想是不存在均摊时间$n^{2-\Omega(1)}$的算法。
• 平面图动态APSP。目前最好的在线算法是$O(n^{2/3})$修改/询问时间。离线算法可以做到$O(\sqrt{n})$。
• 动态维护匹配、极大独立集、$(\Delta+1)$-染色。在oblivious adversary模型中，这些问题有不错的算法，但是这些算法在adaptive adversary模型中就不工作了。（但是，并不是说这些问题在adaptive adversary下就是困难的。我们只是不知道。。。）
• 一些其他的分隔oblivious adversary和adaptive adversary的问题。这些问题比较artificial，是专门为了分隔这两个模型而提出的。

Jan介绍了他和合作者在动态矩阵算法方面的工作。他们搞了不错的动态矩阵算法，然后利用这些算法加速了一些迭代方法，例如内点法（interior point method，IPM）。最经典的（用于求线性规划的）IPM中，我们需要做$\sqrt{n}$次迭代，每次迭代需要计算一个长这样的式子：$A(A^{\sf T}{\rm diag}(\vec{d})A)^{-1}A^{\sf T}\vec{v}$。这个式子需要$O(n^\omega)$时间才能算出来，所以总的时间复杂度是$O(n^{\omega + 0.5})$。但是，每次迭代中，矩阵$A$不会变，且$\vec{d}$和$\vec{v}$只会有一些地方被改变。所以Jan和合作者的想法是：用数据结构来维护式子$A(A^{\sf T}{\rm diag}(\vec{d})A)^{-1}A^{\sf T}\vec{v}$，支持对$\vec{d}$和$\vec{v}$的修改！

虽然这个式子看上去很复杂，但是可以把它规约到矩阵求逆：有一个动态矩阵$N$，每次改变$N$的一个值，要求维护$N^{-1}$。（$N$可以由$A$、$\vec{d}$、$\vec{v}$用某种巧妙的方法拼成。事实上不论多么复杂的式子$f(A_1, A_2, \dots, A_k)$，只要可以用常数次加法、乘法、求逆计算，动态维护$f$就可以规约到动态维护矩阵求逆。）

我们可以用Woodbury等式来维护$N^{-1}$。我们把上一次计算$N^{-1}$时的矩阵$N$就记为$N$，把现在的矩阵$N$记为$N'$。如果这两个矩阵之间有$k$个修改，那么可以写出一个$n\times k$的矩阵$U$和一个$k\times n$的矩阵$V$，使得$N' = N + UV$。根据Woodbury等式：

\[(N+UV)^{-1} = N^{-1} - N^{-1}U(I+V^{\sf T}N^{-1}U)^{-1}V^{\sf T}N^{-1}.\]

因为$U$每一列只有一个元素，$V$每一行只有一个元素，所以$V^{\sf T}N^{-1}U$可以在$O(k^2)$时间内算出来。于是：

• 我们每次修改时计算$A = U(I+V^{\sf T}N^{-1}U)^{-1}V^{\sf T}$，询问$(N+UV)^{-1}$的第$(i,j)$个元素时计算$N^{-1}_{i*}AN^{-1}_{*j}$，即可做到每次修改复杂度$O(k^\omega)$，询问复杂度$O(k^2)$。我们把这个叫做策略I。
• 同理，我们可以每次修改时计算$B = N^{-1}A$，询问时计算$BN^{-1}_{*j}$，即可做到每次修改复杂度$O(nk)$，询问复杂度$O(k)$。我们把这个叫做策略II。
• 我们也可以每次修改时计算整个矩阵（即$BN^{-1}$），即可做到每次修改复杂度$O(n^2)$，询问复杂度$O(1)$。我们把这个叫做策略III。

我们的动态维护矩阵求逆的算法如下：首先查看一下$k$的值，也就是说距离上一次计算$N^{-1}$过去了多少个修改。如果修改的个数太大，我们就用策略III更新$N^{-1}$。否则我们用策略I回答询问。据Jan说，当$\omega\approx 2.38$时，把这个求逆算法和IPM结合起来即可得到$O(n^\omega)$的线性规划算法。（当$\omega$很接近$2$时复杂度会变成$O(n^{2+1/6})$。）如果我们把策略II也考虑进去的话，我们能得到一个$\omega=2$时只需要$O(n^{2+1/18})$时间的算法。